Justin Wolfers presents this graph that he (along with Eric Bradlow, Shane Jensen, and Adi Wyner) made comparing the career trajectory of Roger Clemens to other comparable pitchers:
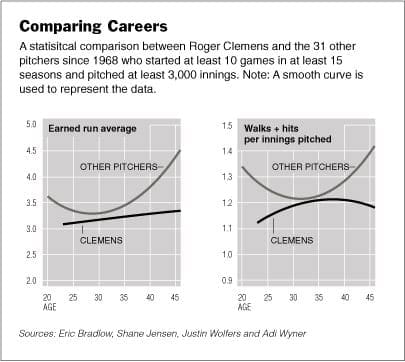
The point is that Clemens did unexpectedly well in the later part of his career (better earned run average, allowed fewer walks+hits) compared to other pitchers with long careers. This in turn suggests that maybe performance-enhancing drugs made a difference. Justin writes:
To be clear, we don’t know whether Roger Clemens took steroids or not. But to argue that somehow the statistical record proves that he didn’t is simply dishonest, incompetent, or both. If anything, the very same data presented in the report — if analyzed properly — tends to suggest an unusual reversal of fortune for Clemens at around age 36 or 37, which is when the Mitchell Report suggests that, well, something funny was going on.
I can’t comment on the steroids thing at all, but I will say that I’d like more information than are in the graphs. For one thing, Clemens is clearly not a typical pitcher and never has been. At the very least, you’d like to see the comparison of his trajectory with all the other individual trajectories, not simply the average. For another, the graphs above seem to be relying way too much on the quadratic fit. At least for the average of all the other pitchers, why not show the actual averages. Far be it from me to criticize this analysis (especially since I am friends with all four of the people who did it!)–this is just a recreational activity, and I’m sure these guys have better things to do than correct ERA’s for A.L./N.L. effects, etc.–but I think you do want to have some comparisons of the entire distribution, as well as a sense of how much the “unusal reversal around ages 36 or 37” is an artifact of the fitted model.
P.S. to Justin, Eric, Shane, and Adi: Now youall have permission to be picky about my analyses in return. . . .
P.P.S. Nathan made this plot showing data from the 16 most recent Hall of Fame pitchers.
Graphing Clemens' ERA against others' without smoothers is a little less compelling:
http://flowingdata.com/2008/02/11/comparing-roger…
Let's see
1. Not showing actual data
2. Quadratic fit
3. No showing of the error band around the data (or the fit)
Anybody planning on a new chapter in "How to Lie with Statistics")? This is the type of distortion Huff wrote about, updated 50 years.
I can't judge Clemens either, but the stats are no more than suggestive.
A lot more discussion of this at http://www.sabernomics.com/
The quadratic plots are absolutely terrible, embarrassingly bad; among the worst statistical graphics I have seen this year. They tell us nothing about what they are supposedly trying to tell us — that Clemens is and has always been highly unusual — because we can't see what any of the other pitcher performances have been. Since they show us nothing about the inter-pitcher variability (nor do they try) we can't se how much of an outlier Clemens is. Also, doing a quadratic fit doesn't even seem to make sense, since it seems likely that the quadratic term will be dominated by a few bad years at the end of the pitcher's career.
The plot Nathan made for the HoF pitchers is much, much better, and just confirms how incredibly lousy the Bradlow et al. plots are.
Andrew, I'm kinda indignant that you didn't call a spade a spade here, soft-pedaling your criticism to avoid offending your friends. I might feel differently when it's my work that is being criticized…but I like to think that I would never do anything this poor, and that if I did, I would be smart enough to ask you not to present it at all!
It may be that the differences in the graphs comes not so much from the smoothing of the data, but from the different data sets that were used. Wolfers et al compared Clemens to "31 other pitchers since 1968 who started at least 10 games in at least 15 seasons and pitched at least 3,00 innings". That's pretty selective. In fact, I'm a bit surprised that they even found 31 such pitchers.
Nathan, on the other hand, uses a set of 16 recent hall of fame pitchers.
I'd like to see smoothed and unsmoothed data from both sets compared to Clemens.
I think JC Bradbury's analysis tinyurl.com/2nu9k7 (www.sabernomics.com)
was much more convincing than Wolfer's. I like the first comment as well.
Phil,
1. I'm sympathetic to the difficulties of getting any sort of graph in to the New York Times; maybe this was the most they could get in there.
2. The fact that they're my friends (and that they've done good work in the past) is relevant: I suspect that if they made what seems like an obvious mistake in their analysis, they'd realize it.
And, to be fair to me, I'm not promoting their work–it was already in a blog with 100 times the circulation of this one–I'm trying to make some constructive suggestions.
I'm afraid that any discussion of the "statistical report" on Clemens' career is to legitimize an atrocious effort to muddy the waters. There is no way to mince observational data (with obscured treatments that may or may not have happened) to answer the question of did he, did he not. Even if it could be proven that Clemens' career was no different than other pitchers, it would not prove that he did not take steroids. This is a case of more data, less information.
You'd like more information? Well, the more detail, the harder to see the big picture. I don't grasp your weighting scheme here. For a NY Times article I would want a lot of impact.
The quadratic fit is based on prior knowledge that athletes in this situation get better then worse. It does a good job of summing up that knowledge. I don't think there's any evidence for a more complex function (e.g., cubic) of performance vs time. If you would say why the quadratic is likely to be a poor summary, that would be interesting.
I would have used loess. Partly because I don't want to think hard and also because there's no reason to think the curvature of the early improvement and later decrement should be the same.
Kaiser,
I agree completely. At points in his article, Wolfers made that same point–he's demonstrating the weakness of Clemens's report rather than trying to prove anything affirmatively himself. At other points, Wolfers unfortunately can't resist going beyond the evidence (at least, beyond the evidence he presented) to claim that that data prove that there was something fishe going on "around age 36 or 37."
Seth,
1. I don't have an explicit weighting scheme. But the graph (a) didn't convince me and (b) left me more suspicious than ever that the model was driving the data.
2. I agree that lowess is better. There's no reason to fit any polynomial at all to the data. The trouble with the quadratic fit is the tail-wagging-the-dog problem: when the model does not fit, inference for the area of interest (in this case, after 36 years of age) can be influenced by data from far away. Basically I'm giving the reason that you give for preferring lwess.
Perhaps if someone conducts a test like Ashenfelter's famous absentee ballots and voter fraud in East Pennsylvania using prediction intervals things could make sense.