Greg Mankiw has a nice little discussion of the difficulty of evaluating the effects of interventions in the n=1 setting:
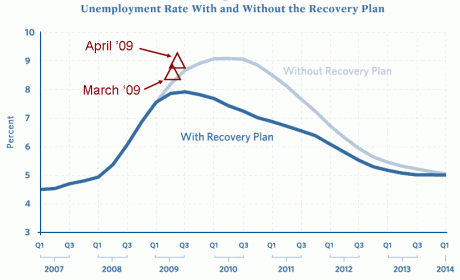
As Mankiw points out, the bad news about the unemployment rate is bad news with or without the recovery plan and thus–although it certainly seems to knock down the predictions shown in that graph–it does not provide much information on the causal effect of the fiscal stimulus. Especially given that the graph comes from a report released in early January, before anyone knew what would end up being included in the final version of the stimulus plan.
As Mankiw writes, this is “a reflection of the inherent uncertainties associated with macroeconomics.” It’s a tough problem, because decisions have to be made, and these decisions will implicitly or explicitly be based on causal inference. It’s just that much of this inference has to be done from model-based extrapolation rather than from clean “natural experiments” whose results we can all agree on.
P.S. I’m wondering a little bit about the placements of the points on the graph. First, I’d recommend against using triangles as a graphing symbol! Is the exact value supposed to be in the middle of the triangle, or maybe the top vertex? I think dots would be better. Second, I can’t quite follow the x-axis. The graph places March halfway between Q1 and Q3, but is that right? I’d think that halfway between Q1 and Q3 would be the center of the year, that is, June/July. But I could be missing something here; I don’t have experience working with this sort of data.
P.P.S. This is an interesting example of a graph where perhaps it’s actually appropriate for the y-axis not to go down all the way to zero, if we accept 3% as some sort of lower bound on unemployment in normal circumstances.
The federal fiscal year runs from Oct. 1 to Sept. 30, so the placement is correct. Not sure why it is that way…
If the world's best wrestler and the world's best boxer each made an economic recovery plan, which one would be better?
For goodness' sake, it's a line graph. It's perfectly acceptable for a line graph, or a scatter graph, not to include the zero value in its vertical scale. The lines encode relative position; they are what S. S. Stevens in the 1940s called an *interval* quantity.
This whole nonsense about scales always having a zero is partly a misunderstanding of Cartesian spaces (the idea that the scales always have to be placed on the x=0 and y=0 lines– they don't) and partly a misunderstanding of the fact that you should never have a *bar* graph that starts any place other than zero, because bars encode a *ratio* quantity, in Stevens' terminology.
Even then, it's permissible if the bars are floating instead of grounded. Then, all that's required is that the whole bar be visible. Come to think of it, that's the rule for grounded bars too, from which "show the zero" rule falls out naturally. The rule is, if you're using bars to encode quantity, you must show the whole length of the bar.
Derek: I agree that graphs don't have to go down to zero. That said, sometimes the positions of the axes can convey information, and we might as well make use of this.
In this case, as I noted above, I think 3% is a reasonable place to put the x-axis. 0% would also make sense, but in many ways, 3% is even better.
I take it from March 09 and April 09 that the short term forecast was wrong so there is no chance for the long term forecast to have any meaning at this point. The title Difficulty in Forecasting, hits the nail square on the head.
Agreed, the triangles could be smaller.
Do the predictions of with and without economic recovery plans have any uncertainty bands about them? Maybe they are actually indistinguishable. Or are the predictions so precise they the uncertainties are masked by the width of the lines?
Same question on the points: Are they as precise as they look? Or are they uncertain blobs?
Jan, you make an excellent point. It is likely the two curves fall within the 95% prediction intervals of each other. Perhaps the datapoints shown are also within the prediction intervals. With n=1 there is no reduction in the interval due to sample size.
This reminds me of a comment I made in a macroeconomics class that rather disturbed the professor. I remarked that it seemed to me that economists and recessions were a bit like doctors (general practitioners) and patients. Each recession that comes along has its own quixotic causes–case histories as it were–and the results of any medication and treatment, while likely to work, could always have disastrous consequences. He said that he thought I'd underestimated the precision economists could accomplish. I told him that I felt he'd underestimated medicine.
Our
paper has a method for evaluating the effects of interventions in the setting with a single treated unit. Not sure whether it would work well in the case of the recovery plan, however, since it may be difficult to create a reasonably similar synthetic U.S. as a convex combination of other countries. It works very well for estimating the effect of the smoking ban in California and the German reunification.