Jerzy Wieczorek has an interesting review of the book Graph Design for the Eye and Mind by psychology researcher Stephen Kosslyn. I recommend you read all of Wieczorek’s review (and maybe Kosslyn’s book, but that I haven’t seen), but here I’ll just focus on one point. Here’s Wieczorek summarizing Kosslyn:
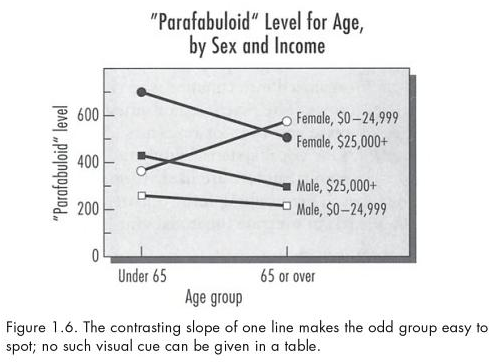
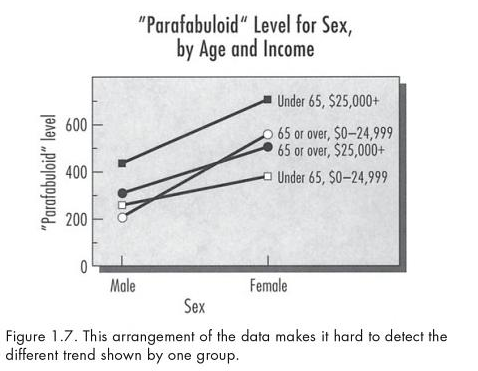
p. 18-19: the horizontal axis should be for the variable with the “most important part of the data.” See Kosslyn’s Figure 1.6 and 1.7 below. Figure 1.6 clearly shows that one of the sex-by-income groups reacts to age differently than the other three groups do. Figure 1.7 uses sex as the x-axis variable, making it much harder to see this same effect in the data.
As a statistician exploring the data, I might make several plots using different groupings… but for communicating my results to an audience, I would choose the one plot that shows the findings most clearly.
Those who know me well (or who have read the title of this post) will guess my reaction, which is that Kosslyn is trying to cram too much into a single graph. The circles and squares are hard to tell apart, the open and dark symbols are a bit confusing, and the lines are so thick that it’s hard to make out the symbols anyway. In addition, the y-axis seems a bit over-labled, with hash marks at every 100. As Kossyln himself notes, the purpose of a graph is to make comparisons, not to be used as a look-up table.
The structure of the (hypothetical) data being displayed is pretty simple: it’s a single continuous outcome as a function of three binary inputs. Displaying this as four lines is just too much. In general I prefer to put continuous predictors on the x-axis and discrete predictors as separate lines, so that would rule out Kosslyn’s second graph (Figure 1.7 above). But Figure 1.6 is too busy. Let’s try it as two graphs:
That looks better. (I’ve also removed the bit about $24,999, which to me just gives a bunch more meaningless numbers for someone to stare at, distracting them from the patterns in the data.) I kept the two graphs on a common scale so we can make comparisons between them if we’d like.
Or we could do it the other way:
That works too. Maybe it’s not quite as good as my other graph, from Kosslyn’s perspective of emphasizing that one discordant line. On the other hand, in real data, the slopes of different lines are estimated with error, and it’s not clear how much emphasis we really should be placing on a line that happens to have a different slope than some other lines whose slopes may not be statistically significantly different from zero in any case.
Here’s another point not mentioned by Kosslyn (or, to be precise, not mentioned in Wieczorek’s review): What’s with those binary age and income variables? That looks like something we’d see in an old-style statistics textbook. I’d prefer more granularity in the continuous variables. Why just “under 65” and “65 and over”? Similarly, why only two income categories. I’d like to have at least three categories, maybe more, depending on how many data points are behind these numbers. In the above graph, it would be trivial to increase the number of age categories on the x-axis, and we could also increase the number of income categories by simply placing more graphs side by side. We could even introduce another background variable (for example, ethnicity) by stacking these graphs in rows (as we did for our maps of voting by income, ethnicity, and state).
The above is not meant to disparage Kosslyn’s work, nor am I suggesting that my redrawn graphs are perfect. Here I’m focusing on one single point, which is the virtue of small multiples (as Tufte puts it). I agree that psychology research should be central in helping us figure out how to convey information, to ourselves as well as to others (I don’t believe in the distinction between exploratory and presentation graphics). No amount of introspection, speculation, and theorizing by Tufte, me, or anybody else can substitute for hard research in perception. I just think that all of use get stuck in our ways of thinking, and I fear that Kosslyn has been stuck in the traditional idea that all the information should be conveyed in a single plot.
Hence I also object to Wieczorek’s statement, “for communicating my results to an audience, I would choose the one plot that shows the findings most clearly.” Sometimes one plot will do, but other times you can make a single display with several plots to better make your point. “A single display with several plots . . .”: that sounds complicated. But as the example above illustrates, the small-multiples display can be cleaner than the one graph.
Oddly enough, I think Kosslyn recognizes this point in some contexts, because in his book on powerpoint, he writes, in reference to the notorious tour de force graph of Napoleon’s troops in Russia:
I [Kosslyn] agree that M. Minard was amazingly clever and managed to cram a huge amount of information into a single display, but I can’t agree that this is an effective way to communicate; the display doesn’t present the facts so that they’re clear or easily absorbed. If you are in the mood, you may enjoy taking the time to study the display for the fun of solving a puzzle, pondering intricate details, or appreciating the graphic devices employed. But if you want the facts and want them in a clear, easily understood way, this display is not the solution.
I just think Kosslyn needs to take the next step and recognize that, in his own field, you can get a cleaner picture with small multiples than by trying to fit all the information on a single plot. As I tell my students: One slide, several plots. One page, several plots. Take advantage of our visual system’s ability and inclination to look around compare.


I’m pretty sure Kosslyn is aware of this and is a proponent of small multiples – although I will only provide hearsay as I have not read his book. In Carr and Pickle’s Micro Map book they motivate small multiples by showing an example of a line graph with 6 lines, and then show two small multiples (using ~ the same amount of area) that are much easier to decode. They cite the example as taken near verbatim from Kosslyn’s Elements of Graph Design.
Here I wrote a blog post showing the referred to picture, . If I remember correctly Carr and Pickle suggest any line graph with more than 4 lines is too many – I’m not sure if the motivation for 4 though came from Kosslyn or somewhere else.
Another good point with this too is that the small multiples don’t necessarily take up more space. You could easily shrink your nice example of small multiples smaller than the original picture from Kosslyn and still (pretty easily) see the same numeric information (just the labels would by necessity need to be smaller).
hmm – my link to my post I mentioned seems to have disappeared – here it is again, http://stats.blogoverflow.com/2011/12/andyw-says-small-multiples-are-the-most-underused-data-visualization/, (hopefully it sticks around this time).
Thank you for the thought-provoking feedback, Andrew.
I’m pretty sure Kosslyn’s main point here was simply that, sometimes, switching your x-axis variable and your grouping variables can make your graph a lot clearer. Of course he could have chosen a better example to illustrate this.
But I absolutely agree with you, and I’m sure he would too, that small multiples are more effective than a single, too-busy graph. Still, given data with complex relationships, even after I’ve already faceted it into small multiples, each small multiple may still need to show groupings by some categorical variable. When that happens, I like to play with switching around the grouping, faceting, and x-axis variables to see which combinations makes for a better graph than the others.
Also, thanks for your objection to my statement that “I would choose the one plot…” Let me revise that: IF I can find one plot (or set of small multiples with consistent x, y, and grouping variables) that tells the story well, THEN I can save space / time / mental energy by showing that one plot (or set of plots). If instead I try to show the same data several ways (“So last time x was age and the groups were by sex, but now the groups are by age and x shows sex, got it?”), and it doesn’t convey any new information, that’s unnecessary cognitive load on my audience.
PS — since you said that “Displaying this as four lines is just too much,” I can’t resist pointing out that your redesigns also have four lines :)
I think my review’s penultimate bullet also shows we’re in agreement!
“The way to avoid lying with statistics isn’t to choose “the right comparison” — it’s to make and present all of the comparisons.”
I think your second two-up graph illustrates the discordant line as clearly as the original all-in-one. In the original — if it some of the line weights, etc, were adjusted — you’d see that there was a discordant line at a glance, but then you’d have to spend a moment to figure out the categories and which one was the different one. In your second graph, you quickly see the categories, and have to do a quick back-and-forth glance to be certain that Low Income Women are the odd category out. Overall, your second graph is ultimately faster and less prone to error.
The “fatal flaw” in your second graph is that it takes twice as many clicks in Excel as the original. (Theorizes the non-Excel-user.)
One issue I’ve had in designing graphics is the wide range in the ability of the audience to understand them, even in the relatively sophisticated world of academia. In the public health/clinical research world there are lots of people, lots of researchers even, who do not see the patterns that are so obvious to us.
Also, there are medical school faculty who freak out at the sight of a line drawn between two points representing categories! You can’t do that!
It’s interesting how social scientists think of graphs as comparisons and not look-up-tables. In engineering it’s quite common to use a graph as a look-up-table. It can be a LOT more effective than an actual look up table in terms of information per page (for example). For a graph-as-lookup-table it’s reasonable to expect say 2 significant digits of accuracy with a third that’s moderately uncertain but sometimes worth interpolating. I would rarely complain about too-many hash marks, though I do find the style of many engineering graphs with a ton of light grid lines too difficult to read. Here are some examples:
http://en.wikipedia.org/wiki/File:Moody_diagram.jpg
(this would be better with very light but not dashed grid lines I think, the dashing actually draws the eye)
http://www.spiraxsarco.com/images/resources/steam-engineering-tutorials/2/3/Fig_2_3_5.gif
That one is horrible, although the information it’s trying to convey is a bit difficult to convey I think also the design of the graph could benefit a LOT from some visual improvements.
The utility of those graphs in Engineering is a legacy though of pre-Computer eras. Nowadays, it’d be much easier to fit several splines and code it all as a far more accurate lookup table.
Pingback: Graph Design for the Eye and Mind, Stephen Kosslyn | Civil Statistician
I ordered one of Kosslyn’s earliest books, but I wasn’t very happy with it; it seemed to be a run-through of some principles that are better covered in books by e.g. Few, Wainwright, or Tufte, together with some opinions I disagreed with. As the old joke goes, what I agreed with wasn’t new to me, and what was new, I didn’t agree with. Perhaps his latest works go deeper now.
I think in this case the reason the age and income were turned into binary categories was so that Kosslyn could discuss what order to present binary categories in, so I’m not too bothered by the practice in this one case.
I disagree with Wayne’s comment about the number of clicks it takes to make an Excel graph, because I think that, where there’s one graph maker and many readers, the trade-off should clearly be to spend extra effort making a good graph, if it saves a dozen readers from having to go to a lot of effort to properly read it. As it happens, I think a skilled user could quickly make one Excel graph that did the job Andrew wanted it to do, without having to create two charts and align them; it’s all in one Excel Line Chart type, just a different table layout: like so…
Kosslyn four lines version:
Men Women
High Income Low Income High Income Low Income
Under 65 400 300 700 400
Over 65 300 250 450 500
Gelman two lines twice version:
High Income Low Income
Men Under 65 400 300
Over 65 300 250
@lt;spacer>
Women Under 65 700 400
Over 65 450 500
Apologies for bad formatting, I hope the result is clear: run Excel Chart Wizard, select Line chart type, select table orientation by Columns, and voila. The secret is in the blank row labeled @lt;spacer>, that breaks the charts lines in two.
As a general point, the horizontal axes are categories, but joining the points with lines makes it look as though there is some sort of trend or link between them. Most chart users are conditioned to think this way, and though with careful reading one can seewhat’s going on I think this is a dangerous practice, and the first thing I would do is get rid of the lines.
I think your two words “trend” and “link” are very important. As you say, most people will be tempted to interpret two points joined by a line as the trend in a continuous variable. There isn’t a *trend* in the graphs: Parafabuloid does not necessarily decline with age and it even if it did there’s no reason to believe it’s a linear decline.
However, I believe there is a *link* in the graphs. In the first graph, looking at the Women graph and the High Income line, I see the line as representing all High Income Women, a trait shared (a link) by women over 65 and women under 65. Those two subgroups have different levels of Parafabuloid, but the are linked by gender and income.
For reference, I try to think of how I’d interpret Andrew’s graphs versus how I’d interpret grouped bar charts. In some sense, I’d still draw an imaginary line from the top of the High Income (Women) Under 65 bar to the top of the High Income (Women) Over 65 bar and compare that to other imaginary lines. I’d still initially think something “look how much Parafabuloid levels increase as low-income women get older, while they decrease as high-income women age.”
There seems to be a connection (sort of) to this illusion (PDF) (HT: Arhur Charpentier. I’m riffing off this line in your post, I think: “it’s not clear how much emphasis we really should be placing on a line that happens to have a different slope than some other lines whose slopes may not be statistically significantly different from zero in any case.” Putting accidentally converging lines on the same graph creates the illusion of an effect that may not be there?
I’m a fan of using lines to join data points across categories; I think eliminating them causes more problems than it solves (“where’s the corresponding point in the next category over? oh, it’s the one with the same shape… What shape is that? let me check the legend…”)
The most stunning use of lines to join up points across categories is Alfred Inselberg’s “parallel coordinates” graph type. This can display dozens of entities across dozens of dimensions (each dimension being a category on the horizontal axis) showing relationships between each entity. Get rid of the lines, and the task would be impossible.
If people are conditioned to see trends, maybe we need an intervention to deprogram them :-)