Michael Betancourt will be speaking at UCLA:
The location for refreshment is in room 51-254 CHS at 3:00 PM.
The place for the seminar is at CHS 33-105A at 3:30pm – 4:30pm, Wed 6 Mar.
[“CHS” stands for Center for Health Sciences, the building of the UCLA schools of medicine and public health. Here’s a map with directions.]
Title of talk: Stan: Practical Bayesian Inference with Hamiltonian Monte Carlo
Abstract: Practical implementations of Bayesian inference are often limited to approximation methods that only slowly explore the posterior distribution. By taking advantage of the curvature of the posterior, however, Hamiltonian Monte Carlo (HMC) efficiently explores even the most highly contorted distributions. In this talk I will review the foundations of and recent developments within HMC, concluding with a discussion of Stan, a powerful inference engine that utilizes HMC, automatic differentiation, and adaptive methods to minimize user input.
This is cool stuff. And he’ll be showing the whirlpool movie!
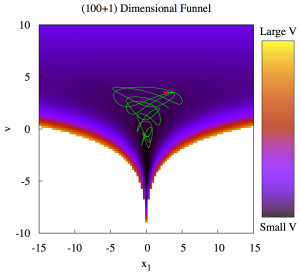
Pardon the NSFW comment, but that graph looks a lot more like the curvature of the anterior than the posterior.
What’s the green squiggly pathology?
That’s a Riemannian manifold Hamiltonian trajectory for the funnel. It’s not a pathology but rather an efficient exploration of the neighborhood of high probability density.
Cool, I’ll be looking forward to hear the talk
Can you make a copy of the whirlpool video available? It looks pretty cool from the screencap :-)
We’ll try to post some videos after the talk.
I’ll be there!
I’m very fortunate that just when my work required the use of STAN (which I was only theoretically familiar with) two talks come into existence to get me up to speed. First the presentation at the LA R User Group last week, and now this one.
UCLA CHS – Center for Health Sciences. The building houses the School of Public Health, Medical School, Dental School, and used to house the UCLA hospital. The public health school has a Department of Community Health Sciences, another CHS, so the confusion is understandable.
Thx.