Lasso and me
For a long time I was wrong about lasso.
Lasso (“least absolute shrinkage and selection operator”) is a regularization procedure that shrinks regression coefficients toward zero, and in its basic form is equivalent to maximum penalized likelihood estimation with a penalty function that is proportional to the sum of the absolute values of the regression coefficients.
I first heard about lasso from a talk that Trevor Hastie Rob Tibshirani gave at Berkeley in 1994 or 1995. He demonstrated that it shrunk regression coefficients to zero. I wasn’t impressed, first because it seemed like no big deal (if that’s the prior you use, that’s the shrinkage you get) and second because, from a Bayesian perspective, I don’t want to shrink things all the way to zero. In the sorts of social and environmental science problems I’ve worked on, just about nothing is zero. I’d like to control my noisy estimates but there’s nothing special about zero. At the end of the talk I stood up and asked Trevor Rob why he thought it was a good idea to have zero estimates and he Trevor Hastie stood up and said something about how it can be costly to keep track of lots of predictors so it could be efficient to set a bunch of coefficients to zero. I didn’t buy it: if cost is a consideration, I’d think cost should be in the calculation, the threshold for setting a coefficient to zero should depend on the cost of the variable, and so on.
In my skepticism, I was right in the short term but way way wrong in the medium-term (and we’ll never know about the long term). What I mean is, I think my reactions made sense: lasso corresponds to one particular penalty function and, if the goal is reducing cost of saving variables in a typical social-science regression problem, there’s no reason to use some single threshold. But I was wrong in the medium term, for two reasons. First, whether or not lasso is just an implementation of Bayes, the fact is that mainstream Bayesians weren’t doing much of it. We didn’t have anything like lasso in the first or the second edition of Bayesian Data Analysis, and in my applied work I had real difficulties with regression coefficients getting out of control (see Table 2 of this article from 2003, for example). I could go around smugly thinking that lasso was a trivial implementation of a prior distribution, coupled with a silly posterior-mode summary. Meanwhile Hastie, Tibshirani, and others were moving far ahead, going past simple regressions to work on ever-larger problems. Why didn’t I try some of these prior distributions in my own work or even mention them in my textbooks? I don’t know. Finally in 2008 we published something on regularized logistic regression, but even there we were pretty apologetic about it. Somehow there had developed a tradition for Bayesians to downplay the use of prior information. In much of my own work there was a lot of talk about how the prior distribution was pretty much just estimated from the data, and other Bayesians such as Raftery worked around various problems arising from the use of flat priors. Somehow it took the Stanford school of open-minded non-Bayesians to regularize in the way that Bayesians always could—but didn’t.
So, yes, lasso was a great idea, and I didn’t get the point. I’m still amazed in retrospect that as late as 2003, I was fitting uncontrolled regressions with lots of predictors and not knowing what to do. Or, I should say, as late as 2013, considering I still haven’t fully integrated these ideas into my work. I do use bayesglm() routinely, but that has very weak priors.
And it’s not just the Bayesians like me who’ve been slow to pick up on this. I see routine regression analysis all the time that does no regularization and as a result suffers from the usual problem of noisy estimates and dramatic overestimates of the magnitudes of effect. Just look at the tables of regression coefficients in just about any quantitative empirical paper in political science or economics or public health. So there’s a ways to go.
New lasso research!
Yesterday I had the idea of writing this post. I’d been thinking about the last paragraph here and how lasso has been so important and how I was so slow to catch on, and it seemed worth writing about. So many new ideas are like this, I think. The enter the world in some ragged, incompletely-justified format, then prove themselves through many applications, and then only gradually get fully understood. I’ve seen this happen enough with my own ideas, and I’ve discussed many of these cases on this blog, so this seemed like a perfect opportunity to demonstrate the principle from the other direction.
And then, just by coincidence, I received the following email from Rob Tibshirani:
Over the past few months I [Tibshirani] have been consumed with a new piece of work [with Richard Lockhart, Jonathan Taylor, and Ryan Tibshirani] that’s finally done. Here’s the paper, the slides (easier to read), and the R package.
I’m very excited about this. We have discovered a test statistic for the lasso that has a very simple Exp(1) asymptotic distribution, accounting for the adaptive fitting. In a sense, it’s the natural analogue of the drop in RSS chi-squared (or F) statistic for adaptive regression!
It also could help bring the lasso into the mainstream. It shows how a basic adaptive (frequentist) inference—difficult to do in standard least squares regression, falls out naturally in the lasso paradigm.
My quick reaction was: Don’t worry, Rob—lasso already is in the statistical mainstream. I looked it up on Google scholar and the 1996 lasso paper has over 7000 citations, with dozens of other papers on lasso having hundreds of citations each. Lasso is huge.
What fascinates me is that the lasso world is a sort of parallel Bayesian world. I don’t particularly care whether the methods are “frequentist” or not—really I think we all have the same inferential goals, which are to make predictions and to estimate parameters (where “parameters” are those aspects of a model that generalize to new data)
Bayesians have traditionally (and continue to) feel free to optimize, to tinker, to improve a model here or there and slightly improve inference. In contrast, it’s been my impression that statistical researchers working within classical paradigms have felt more constrained. So one thing I like about the lasso world is that it frees a whole group of researchers—those who, for whatever reason, feel uncomfortable with Bayesian methods—to act in what i consider an open-ended Bayesian way. I’m not thinking so much of Hastie and Tibshirani here—ever since their work on generalized additive models (if not before), they’ve always worked in a middle ground where they’ve felt free to play with ideas—rather, I’m thinking of more theoretically-minded researchers who may have been inspired by lasso to think more broadly.
To get back to the paper that Rob sent me: I already think that lasso (by itself, and as an inspiration for Bayesian regularization) is a great idea. I’m not a big fan of significance tests. So for my own practice I don’t see the burning need for this paper. But if it will help a new group of applied researchers hop on to the regularization bandwagon, I’m all for it. And I’ve always been interested in methods for counting parameters and adjusting chi-squared tests. This came up in Hastie and Tibshirani’s 1990 book, it was in my Ph.D. thesis, and it was in my 1996 paper with Meng and Stern. So I’m always happy to see progress in this area. I wonder how the ideas in Tibshirani et al.’s new paper connect to research on predictive error measures such as AIC and WAIC.
So, although, I don’t have any applied or technical comments on the paper at hand (except for feeling strongly that Tables 2 and 3 should really really really be made into a graph, and Figure 4 would be improved by bounding the y-axis between 0 and 1, and really Tables 1, 4, and 5 would be better as graphs too (remember “coefplot”? and do we really care that a certain number is “315.216”), I welcome it inasmuch as it will motivate a new group of users to try lasso, and I recommend it in particular to theoretically-minded researchers and those who have a particular interest in significance tests.
P.S. The discussion below is excellent. So much better than those silly debates about how best to explain p-values (or, worse, the sidebar about whether it’s kosher to call a p-value a conditional probability). I’d much rather we get 100 comments on the topics being discussed here.
Does this mean the Lasso will be in the 3rd Edition of BDA? How is it getting along by the way?
Erik:
BDA3 is nearly done. We don’t have any lasso examples, but we do at least mention the idea, which I think is a start. Regarding lasso in general, my current Bayesian view (which I haven’t implemented, so it’s just an idea) is to separate its shrinkage properties from its setting-to-zero properties. Based on the work in my 2008 paper with Aleks, I think the t family makes more sense than the double-exponential for shrinkage. So what I’d like to do is shrink using the t and then have the set-to-zero feature be tuned independently, based on the cost of keeping information.
The lasso (actually the Elastic Net) is my go to tool for high dimensional problems, I’m a huge fan. I’m even working on a coefplot for pulling out the nonzero coefficients from it. Should be done soon.
I was about to bring up the elastic net, which I implemented for my company’s stochastic gradient descent software for logistic regression and CRFs (along with L1, L2, and Cauchy). I like the elastic net’s motivation — it provides identifiability via the L2 (i.e., “ridge”) component and shrinkage to 0 in point estimates via the L1 (i.e., “lasso”) component. With just L1, you get identifiability issues with the kind of strongly correlated parameters you see in natural language data (at least if you analyze it multinomially in terms of word or token frequencies) because the penalty term is just the sum of the absolute values of the coefficients. With just L2, never get to zero because the quadratic penalty drops faster than the coefficients.
L1 regularization has been very popular in the machine learning world. Calling it a cottage industry would underestimate its pervasiveness. Almost nobody calls it “lasso.” Some say (equivalently in terms of estimator) that they’re doing MAP with double-exponential (Laplace) priors. The electrical engineers are all over L1 and call it “compressed sensing” for its motivating application in their world. Even the people fitting SVMs do it, and they rarely even talk about probability.
Hi Bob,
Can you please elaborate on what you mean by “identifiability” issues with L1 regularization?
Thanks
JZ
Sorry for taking so long — I just saw the reply.
If you have two predictors x1 and x2 with perfect correlation, L2 regularization identifies a unique result, whereas with L1 regularization any interpolation between b * x1 and b * x2 (e.g. 0.3 * b + x1 + 0.7 * b * x2) has the same likelihood and the same L1 penalty (namely b). But the L2 penalty is lowest when the two coefficients are equal (lambda * b * x1 + lambda * b * x2). So you get identification.
Wanted to bump this. The elastic net is a fantastic method for regularization and multicollinearity, and I was curious if such tests can be extended to the elastic net. I doubt that it’d be necessarily easily done since a second parameter (the ridge) is added to the minimization. I’d love to hear a response on this.
The idea of setting coefficients to exactly zero is a very powerful one in many domains – especially when the number of features becomes huge – and has been adopted widely in the machine learning community if not amongst Bayesian statisticians. I have a problem where the number of features could be in the hundreds of millions, and where I will be using the learned model in a real-time service with very strict response time guarantees. Having coefficients shrunk to exactly zero vastly reduces both the memory needed to store the model, and the time taken to compute a prediction.
I found in the natural language (sequence) classification problems that the speed comes from the fact that the individual data points are usually sparse (hundreds, maybe thousands of non-zero predictors) despite the millions of predictors in the overall space. That is, I found dense storage of hundreds of millions of coefficients to be more efficient than accessing them randomly during training.
At some point, though, you’ll run out of memory. It wouldn’t have worked for hundreds of billions of predictors, or classification problems with thousands of categories and hundreds of millions of predictors. It also doesn’t work if you get the data streamed to you, rather than in a batch, because then you don’t even know how many predictors you’re going to have.
To eke out even more speed and compactness, I really like John Langford’s approach in his Vowpal Wabbit software, which I blogged about ages ago:
http://lingpipe-blog.com/2008/03/25/symbols-as-hash-codes-for-super-fast-linear-classifiers/
And here are John’s technical links:
http://hunch.net/~jl/projects/hash_reps/index.html
and the GitHub link:
https://github.com/JohnLangford/vowpal_wabbit/wiki/Feature-Hashing-and-Extraction
I first came across the feature-hashing “trick” in the Mahout library, and it struck me as a wonderful solution to two problems:
1) straightforwardly mapping all the features into a known space
2) not knowing how many features you have when you start. (Hashing allows you to make only one pass over the data, rather than having to use a first pass to build a dictionary/count how many different features you have)
For situations with very large numbers of predictors, it’s clearly the way to go.
If one believes that no coefficients are zero then one’s model of anything must include everything. That is, a butterfly in Shanghai can affect who wins the next mayoral election in Springfield.
Whenever we set up a model with a finite number of variables we are already setting a lot of other parameters to zero. Or, if we don’t like that turn of phrase, we could say they are sufficiently close to zero they are irrelevant in the study at hand (i.e. we will treat them as if zeroes). DAGs make this process explicit.
In my view penalized regression makes a lot of sense in applications for which we don’t have much theory to constrain the model.
Fernando:
Of course I am only considering variables that are in my model. I’ve worked on hundreds of applied statistics problems and not once has my model included irrelevancies such as a butterfly in Shanghai. All those other independent variables go into the error term. What I’m talking about are the variables that I’ve already included in my model. And, yes, if I’m modeling hundreds of survey responses given dozens of background variables, I don’t think any of the true coefficients (“true” in the sense of being the values I would get if I could interview the entire population) would be exactly zero. But lots of them would be close to zero, which is the point in practice. In the sorts of problems I work on, there’s nothing really special about zero, but there is a need to regularize our estimates. Lasso has proved very useful for this.
Is it lasso (L1) specifically that’s so useful, or would ridge (L2) regression also have worked?
James and Stein realized you needed regularization in 1961:
http://en.wikipedia.org/wiki/James–Stein_estimator
And back to the Stanford-ers, there’s then the Efron and Morris (1973) analysis, which I love because it’s a binomial example using baseball batting ability.
http://lingpipe-blog.com/2009/11/04/hierarchicalbayesian-batting-ability-with-multiple-comparisons/
Even though Andrew loves baseball, I seem to recall he doesn’t like batting average (ability) examples because the number of at bats is a random variable.
Bob:
L2 isn’t so great because it shrinks by a uniform percentage, thus doing too much shrinkage of big values and not enough shrinkage of small values. To put it another way, I think the true distribution of coefficients is long-tailed, that’s why I think the Cauchy shrinkage worked so well in my paper with Aleks.
The normal distribution can work well for a coherent set of parameters (such as the 8 school effects) but not so well in general. For a default prior, you want to be aiming for the distribution of all possible coefficients, which is something like a scale mixture of a bunch of separate distributions. Take a scale mixture of normals and you get something like a t. This is probably worth a paper (if such a paper hasn’t been written already).
And, sure, the baseball example is ok but my main problem with it is the problem doesn’t feel real to me. The dataset is arbitrarily limited. The 8 schools example, small as it is, was once real. Now, of course, I like those survey examples. There’s still the potential for some good baseball examples, for example predicting next year’s success (maybe OBP or SLG, not batting average!) from last year’s, or something more interesting such as predicting major-league success using minor-league stats. Either way, I’m sure that partial pooling would be the way to go.
I suppose we coudl fit the degrees of freedom while we’re at it.
Without some curvature, you get into identifiability issues. So how about a Cauchy + L1 mashup?
I think the baseball problem is as real as the 8 schools example. You want to know who’s the best baseball player the same way you want to know the effects of coaching.
As someone who came out of computer science, I like predictive modeling. Efron and Morris’s example took something like 50 at-bats from the beginning of the season and tried to predict the rest of the season (and I just love that they used 1970 — a great season).
As I’ve said before, I just love Jim Albert’s Curve Ball, which goes into much more interesting baseball stats at relatively intuitive level (that is, no integrals or even derivatives, but a bit of algebra).
Andrew:
“not once has my model included irrelevancies such as a butterfly in Shanghai”. Yes, and that is my point.
We all make binary distinctions all of the time (in/out of model, connected/not connected), so the criticism that DAGs take a binary approach to causality (e.g. either two variables are connected or not) is neither here nor there. We all do this all of the time.
I agree with you that the lasso is useful, especially for predictions where over fitting is always a problem. Rather my point is I don’t make too much of pervasive continuity. Even if it is “true”, we always make a cutoff.
In my view the more interesting aspect is the tradeoffs that are made when the “cutting off” is made through theory, or penalization, or some combination thereof. Lasso has great appeal bc it can chop its way through a morass of variables, but the danger I see in these approaches is they substitute for theorizing. Maybe that is ok, maybe not. Probably depends on whether we want to predict, explain, or intervene.
Fernando:
I agree. We are always making approximations and shortcuts. I find that, the cruder my inferential tools, the quicker I am to reach for the shortcut. That’s why, in my everyday regression work, I want to move toward routine use of partial pooling, which I think will allow me to more easily include more predictors.
That’s the problem with the whole “noninformative priors” thing. If you don’t have prior information in your prior distribution, you often have to put it in somewhere else, and in a cruder way, such as by preselecting predictors as in or out.
I guess it’s because I work on problems in the physical sciences, but I just don’t see the point of “noninformative” priors. Sure, slightly more diffuse than I really expect… fine, but if I expect a coefficient to be positive and around 1 I certainly don’t put a half cauchy prior with scale 100… I maybe put an exponential prior with scale 5, or if I know it can’t be 0 some kind of gamma model which I tend to think of as being like a sum of exponentials so maybe 1.5 exponentials with mean 1.5 or something.
I try to do order of magnitude analysis ahead of time, and create dimensionless models that already have the overall magnitude of everything somewhere near 1 based on some basic knowledge.
If I find that my posterior for a parameter looks a lot like my prior, I tend to try a refit with an order of magnitude more diffuse prior to make sure that it’s not just my lucky guess.
I think there are really few scientific questions where we can’t at least bound the order of magnitude of some effect.
Daniel:
> If I find that my posterior for a parameter looks a lot like my prior
You might wish to think about using posterior/prior (relative belief) – the shape is not affected by the prior (in full dimensions).
And there is a developed/ing theory for Inference Based on Relative Beliefs http://www.utstat.utoronto.ca/mikevans/research.html
Isn’t that just likelihood? In other words, when the likelihood function is flat in the region of high probability for your prior, the posterior looks just like your prior. Hence, making your prior more diffuse might allow you to find a region of space where the data have more to say. But if your prior encodes real information that you know independent of the data (like for example that a parameter must be positive, or that it must have magnitude less than some particular constant like the speed of light or something) then making your prior “enormously” more diffuse doesn’t make scientific sense (ie. switching from exponential with mean 5 to half cauchy with median 10^6). You should be asking why this aspect of your model is insensitive to data and see if you need a different model.
I’ll look at your link on Relative Beliefs. thanks for the reference.
> Isn’t that just likelihood?
That was my initial and apparently frequent mistake.
It is actually Pr(x|theta)/Pr(x) which equals Pr(theta|x)/Pr(theta).
The right side shows that it is a relative probability rather than a likelihood which instead is a (weird) equivalence class of functions. (Now, it can be _ruined_ into a likelihood by multiplication of an arbitrary constant).
The theory by Mike Evans addresses what can be gained from these relative probabilities.
That may not be of interest to you, but the right side also shows a convenient way to approximate a likelihood if it is not available in closed form (which is the usual case for parameters of interest less tha the full dimension).
A DAG is about laying out explicitly the asumptions behind the joint probability model. Other than that they are completely non-parametric which is to say, compatible with Bayesian estimation and partial pooling.
Why insist on making assumptions transparent? Because mathematically identical models can have very different interpretations. A parameter for an interaction with a proxy has different interpretation than an interaction with a cause when it comes to manipulation, policy.
So I dont consider DAGs crude, or shortcuts. They are complementary, and help avoid ambiguity.
I think a google scholar search for ‘sparse Bayesian regression’ or ‘Bayesian variable selection’ or ‘spike and slab priors’ will produce a lot of results relevant to this discussion.
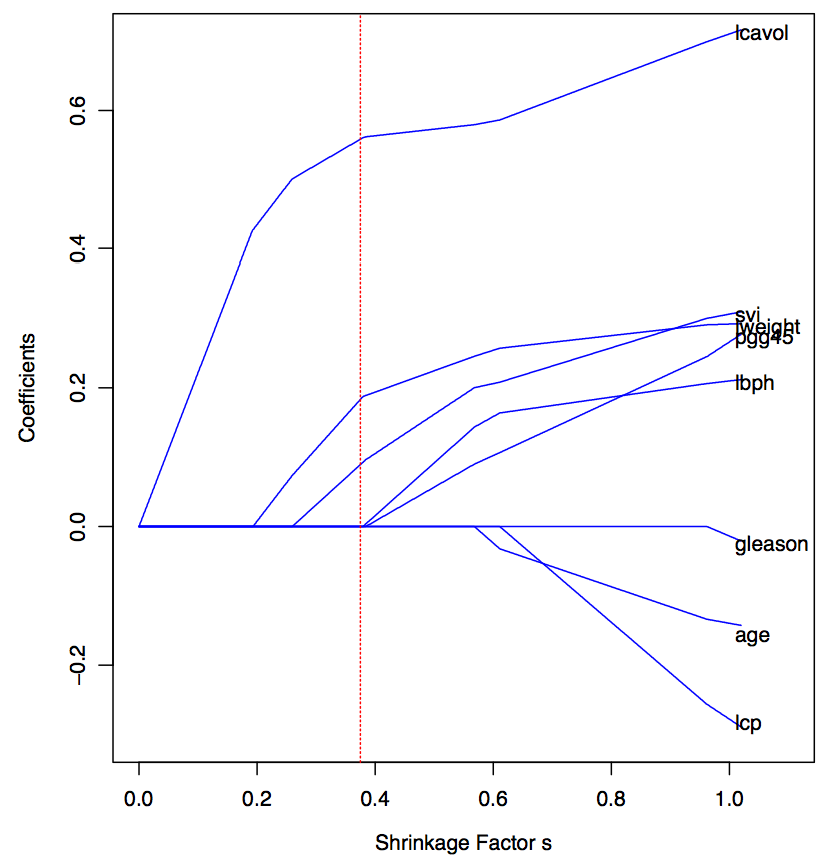
Oooooh, I hate that “spike and slab.” Especially the slab. The key to lasso is that it partially pools in a continuous manner (see graph at top of post, which was taken from Tibshirani’s slides). It’s no slab.
Andrew:
Your comment above,
“Regarding lasso in general, my current Bayesian view (which I haven’t implemented, so it’s just an idea) is to separate its shrinkage properties from its setting-to-zero properties.”
seems to implicate something like a spike-and-slab prior.
Now that I look it up, I see that most of the “spikes” people use are not delta functions at zero, but just relatively “spiky” at zero. This seems very much like the (centered) Laplace/double-exponential distribution, which is also spiky at zero (so spiky it’s not even differentiable) and has fat tails (fatter than Gaussian, not as fat as Cauchy — I see a t-shirt with Gauss, Laplace and Cauchy on it).
I always thought you objected to the spike at zero, not the slab, because of your argument that you don’t expect effects to be zero (for predictors you choose to include, not for butterflies on the other side of the world).
But the Cauchy, which you seem to like, is very slab-like in that it has very fat tails.
Or is it really that you don’t like the sharp transition from spike to slab?
Bob:
No, I’ve always said that my problem with “spike and slab” is the slab, more than the spike. The Cauchy is not so slab-like. Sure, it’s slab-like in the tails. But most of the probability is not in the tails! The Laplace also has that goofy behavior near zero which I don’t like for full Bayes. I can see it working for the purpose of point estimation, but as noted I’d like to separate the zeroing-out from the partial pooling.
I could easily imagine coding up something where if you have a parameter which you expect to be either meaningless, or have size about 1, you could create a prior with two gaussians one with sd=0.05 and say 70% of the probability and one with sd=5 for the other 30% to get something which is not too flat in the region -10,10
The mistake comes where you use a delta function at 0. We had an example like that come up recently, maybe in the last half year on this blog.
I’m just making up the numbers, and if I were going to do this I would certainly be graphing the function and tuning it until it made some sense scientifically. This is informative prior at its best. I view this as a significant strength of the Bayesian method and I really don’t understand why anyone would want “uninformative” priors. To me “somewhat less informative than what my scientific background makes me think” is the best bet. A bit of a mouthful though.
Chapter 13 of the Murphy textbook has a nice discussion on sparse linear models, starting with Bayesian variable selection and progressing to Lasso. There’s an explanation of spike-and-slab along the way too — it’s not the only option for Bayesian variable selection, turns out.
Does this mean that significance testing will be possible for ridge regression too?
P.S. I don’t suppose that understanding any aspects of a paper on significance tests and p-values could be illuminated by “those silly debates about how best to explain p-values”. It’s too bad that most commentators on my remark* (about p-values not being conditional probabilities) saw their goal as needing to find a way to view significance levels as conditional probabilities, rather than trying–just for a second–to see if a different perspective emerges from going with my point. I think it does, and hope to bring out why it is relevant (and not silly) in discussing the evidence for Higgs-like particles on errorstatistics.com.
*Here and on the Normal Deviate’s blog:http://normaldeviate.wordpress.com/2013/03/14/double-misunderstandings-about-p-values/
P.P.S. I don’t waste my time bothering to bring up irrelevancies on people’s blogs. Give me some credit.
Mayo:
When I was talking about silly debates, I wasn’t referring to your comment, I was referring to some endless back-and-forths which were all about terminology. I summarized my view in a comment here on Larry’s blog.
That p-value post itself was a bit “silly” (shallow? ranting?) when compared to an excellent, meaty, technical post like this one.
GIGO. :)
Andrew: That’s part of my comment above, the assumption that it was all about terms and notation kept the discussion shallow. I don’t plan to comment further on this here, but I might note, on your (2):
“If B, then probability of A is X”
is true when the antecedent is false.
The overall statement is not false (which means in binary logic, it’s true), but if ~B then the statement’s truth value is independent of P(A) = X so this statement says nothing about probabilities in that case.
Incidentally, some mathematicians reject the law of the excluded middle over infinite sets for various reasons, it has some interesting consequences.
Frequentists refuse to call them conditional probabilities because they don’t want anyone inverting the distribution with Bayes theorem. In other words, they don’t insist on this point to “add” anything. They insist on it in order to “subtract” Bayesian methods.
This is done on purely ideological grounds, since there is nothing in the mathematics which requires such a restriction, or even hints at one. The mindset seems to be “I’m a really really brilliant Frequentist and I don’t understand what a prior probability is, so therefore it must be nonsense and we need to get rid of it”. That’s the essence of claims like your “they aren’t conditional probabilities because there is no prior or joint” even though others can produce priors and joints all day for them. Talk about not giving people credit!
If you find some insight into P-values, then I’m 100% sure Bayesians will be able to understand it despite the huge handicap, and gross faux pa, of calling them conditional probabilities. I wouldn’t even be surprised if you do find such insight, since although P-values are a disaster as half taught in introductory text books, I believe they often have a stronger Bayesian foundation than is generally realized and sometimes use them myself. So lighten up. There’ll be at least one die hard Bayesian paying attention to your points and trying to understand them.
Hi Andrew,
I have a question about this post which is rather a general question:
Can one use the p-value computed using this method (LASSO) and use it (or a function of it) as a prior for a Bayesian model on the same data?
Let me ask my question more generally, can one use method A (non Bayesian method) on data and computes a parameter (let’s call p) and use a function of this parameter (say h(p)) as a prior for method B (Bayesian) on *the same data* ? I am sorry if it is very stupid question! I am thinking is not OK because it is on the same dataset, what is your opinion?
Thanks,
The usual method for doing this is dividing the data, perhaps taking randomly 20% of the data to fit some stuff using LASSO and using it as input to a full bayesian model on the other 80% or something like that. I suspect that frequentists even believe in this since then the priors come from some kind of frequencies.
Andrew
Thank you for your very generous comments in your blog. Actually it was me (not Trevor Hastie) giving that
lasso talk at the Stanford-Berkeley seminar in 1995. (I guess it wasn’t that memorable!)
But I do remember that you were critical at the time and said something like “why not just do the
full Bayesian Analysis?”.
In my experience, the lasso and the Bayesian Lasso (Park and Casella) give similar
results, but the lasso is much more scalable computationally, due to the convexity of the objective function.
I’ll read with interest other comments that are posted and will be happy to respond or answer questions that are raised.
Rob:
OK . . . I think what happened is that you gave the talk, I asked the question of why do you think zero estimates are a good thing, and Trevor stood up and responded with the comment about cost.
As a researcher in ecology applying these techniques, I’ve always worried about the interpretation of the coefficients in one of these models. As I understand it, the shrinkage adds a bit of bias to estimates of the coefficients whilst reducing their variance and hence you hope to get a lower error model where the variance component is decreased more than the bias component is increased. If the coefficients are biased how should we interpret them in terms of real-world phenomena? Does this bias even matter?
Gavin:
Bias is inevitable in all estimates, least-squares and otherwise. See discussion here.
Thanks for this Andrew, most useful indeed!
We should be comfortable with some bias, but it is also important that we **think about the bias** in the right way. I suspect that the standard interpretation of bias from “shrinkage estimators” is that they bias the estimates toward zero. Under the lasso, this interpretation would require that the Lasso has *already selected the right predictors/covariates*.
In fact, there is a necessary and sufficient condition for the Lasso to select the correct model (asymptotically). It is a stringent condition on the design matrix and if the columns of X are a bit correlated, this condition fails. When p~1000 and the rows of X are multivariate gaussian with constant correlation .1, the condition is not satisfied with very high probability. In many settings, we would be blessed to have so little correlation…. When this condition fails, relevant columns will be ignored and irrelevant columns will be added. This is a really viscous form of bias. Moreover, it is not “asymptotically unbiased” in the high dimensional (p>n) setting.
The bias in model selection is often surmountable. You can . . .
1) “precondition” see here: http://www.stat.wisc.edu/~karlrohe/preconditioning.pdf
my favorite! It simply “de-correlates” the columns with some linear algebra. This method highlights all the various trade-offs that one can make.
2) “hard-threshold” the beta-hat-lasso. see here: http://arxiv.org/abs/1001.5176
You can prove results for this… somehow it seems a bit brash.
3) “adaptive lasso” see here again: http://arxiv.org/abs/1001.5176
It can be thought of as the “more refined” cousin of hard thresholding.
4) use a different (non-convex) penalty. This makes the computation difficult. see here: http://arxiv.org/pdf/1002.4734.pdf
Technically challenging and interesting.
The papers in 2-4 have made significant contributions to the understanding of these techniques.
If one is interested in the assumptions on the design matrix that one needs to make various inferences, this paper (http://arxiv.org/abs/0910.0722) gives a good road map to all the various assumptions. See figure 1 on page 10.
I believe this is the next hot thing, just as Gibbs sampling and MCMC were back in the 90s. Also, I see a circle here: cs guys trying to learn statistics, stat guys trying to learn math, math guys trying to learn cs.
I don’t know anything about the lasso, but it seems from brief reading like you could do something similar with model averaging with point priors (as alluded to above by “Anonymous” (statistics *and* hacking? They have multiple talents!). We use Cauchy priors on standardized effect size, so the priors are decidedly un-slab-like. What’s to stop you from computing a set of Bayes factors for point nulls, sampling from posterior distributions, then using both to average everything toward 0?