Bob writes:
If you have papers that have used Stan, we’d love to hear about it. We finally got some submissions, so we’re going to start a list on the web site for 2.0 in earnest. You can either mail them to the list, to me directly, or just update the issue (at least until it’s closed or moved):
https://github.com/stan-dev/stan/issues/187
For example, Henrik Mannerstrom fit a hierarchical model the other day with 360,000 data points and 120,000 variables. And it worked just fine in Stan. I’ve asked him to write this up so we can post it here.
Here’s the famous graph Bob made showing the scalability of Stan for a series of hierarchical item-response models:
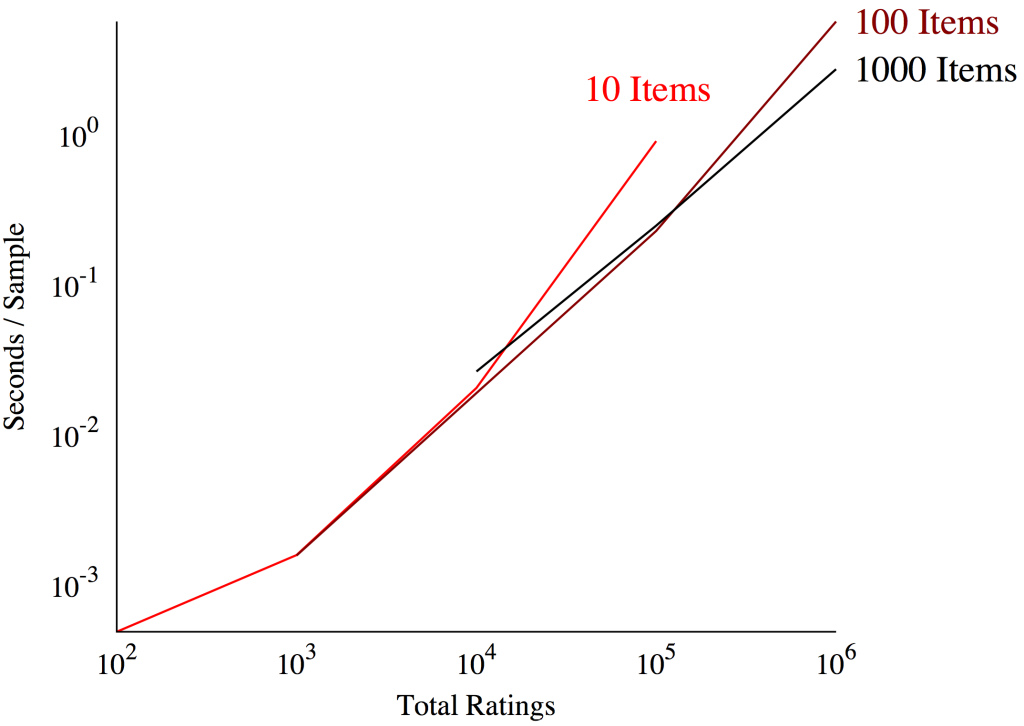
I’m not sure what that graph tells me. Leaving aside the fact that I have no idea what an item response model is, the key question is whether the statistical efficiency of the sampler scales with the data size. (The graph shows that the time for one proposal grows linearly, but not that the amount of time to perform inference of the same quality grows linearly) I would think a more useful graph would be something like Effective Sample Size/time.
I also have problems with the raw reporting of sizes. If the hierarchical model in question is of a latent Gaussian form and most of the parameters are Gaussian (eg there are only O(10) variance-type parameters), that’s not a very big model. Eg you can get the (almost) exact joint for the Gaussian bit conditioned on the data and parameters, deterministically integrate out the non-Gaussian parameters and, if the mood strike you, correct the Gaussian bit with a metropolis step. This should always be more efficient than pure MCMC.
Dan,
I agree that ESS per second would be a better measure. In this particular example I think that the efficiency of the sampler is close to 1, or at least that it does not change much as the scale changes. Regarding your question of what is “a very big model,” this depends on context. So I think what is needed is this sort of scalability analysis for different classes of model. Finally, with regard to your last point, if you have a general way of implementing this idea in Stan, please let us know. The difficulty is that there are various methods that help out in specific problems but we want Stan to be a general tool that does not require additional user programming.
I was thinking about this after I posted the comment. The challenge is the flexibility – it “always works” that if you integrate out some awkward parameters (like variances), the mixing of your chain improves, but I don’t know if there’s any automatic way to do this. But if you could find a (small-ish) set of parameters that you want to integrate out, you could do basically the thing that’s in INLA:
– find the conditional mode for those parameters,
– fan out in a grid (or smarter thing) until you’ve exhausted the main mass of the posterior and compute the appropriate integration rule weights. The trick is that you don’t really need a lot of these to better MC accuracy. (The INLA experience has been that’s is shocking how few values you can get away with!)
– Run parallel chains for each gridded value
– Post-process estimates as weighted sums of the chains.
I’m not so sure on the re-combination step, but something like that should work. (Or, I’m missing something blindingly obvious)
Incidentally, a bunch of classical results on laplace approximations suggest that everything gets easier (ie more Gaussian) as the number of data points increases, which maybe suggests that Big-STAN is only important for “hard” models, rather than limits of classical ones (in the sense that, for reasonable chain lengths, a simple asymptotic approximation will be better or as accurate with a whole lot less computation)
Hmmmm. Would it be better to use parallel chains or use the same randomness for each of the chains? I’ve never really thought about this before.
Also – regarding the last comment, it kinda suggests that you could get superlinear ESS/time scaling on one problems. That’d be a nice “bragging graph” :p
Dan:
We’re actually working on implementing some of this in Stan. It will work automatically, but the user will need to partition the parameters. We call it our “lmer emulator.”
That will be really cool!!!
Incidentally, this this going to be part of a full Laplace approximation push? I know it’s not really a general tool, but in lots of common models (and, more crucially for this sort of thing, model components) it’s a really great thing to do…
That is the plan. We’re also working with David Blei on implementing black-box variational Bayes. It’s possible that the VB will be so good and so general that it will render the Laplace approximation DOA. But I’d like something fast and scalable that reproduces lmer/blmer etc., as a comparison if nothing else.
It’ll be in there, but my money is on the ultimate result being just how poorly these approximations perform relatively to HMC. You just can’t win against high-dimension spaces unless you take them into account a priori, and if you’re in low dimensions you should be able to get everything done with existing software.
That’s not necessarily true. Laplace approximations work perfectly well on Hilbert Spaces whereas HMC takes some care.
There’s also the very real fact that likelihood evaluations get very expensive as the dimension increases (and I would not expect linear scaling of HMC [or anything else] in spatial problems, for example). In that case you’re comparing attainable accuracy with computational budget, which is a much harder call.
In spite of the acronym fairy being asleep when ABC was idiotically coined as an acronym, all (non-trivial) Bayesian computation is very very approximate. Like at best we have one or two significant figures for interesting problems (if you define interesting in such a way that this is true…)
Laplace approximations may have a more immediate translation to Hilbert spaces, but you can’t compare that to HMC without a proper translation of HMC to symplectic Hilbert manifolds which, apologies to Beskos et al. who have made the first steps by looking to parallels with the infinite-dimensional diffusion algorithms, has not yet been achieved (turns out infinite-dimensional symplectic manifolds are weird).
HMC is going to scale as linearly as you’ll get due to its coherent exploration (given a typical implementation you’ll linear scaling modulo a d^{-0.25} penalty, but that only comes from having to compute the trajectories numerically _and_ d has to be really, really big for you to start seeing effects).
The cost of likelihood evaluations is a huge red herring — yes it might take much longer for a single HMC transition, but you’re never going to beat the scaling of ESS/time into high dimensions (Hamiltonian flow is MAGIC). I’d much rather have a few hard-fought HMC iterations than an approximation that drastically limits my modeling flexibility and doesn’t provide that much accuracy in the end (run away once any one mentions “grid” or importance sampling in high-dimensions), and that’s not even taking into account the kinds of model-specific optimizations that can be done for HMC. Plus it forces you into building a model up from simple to complex instead of building a huge model with little understanding of it and throwing it at a black box.
Don’t you need to compute the determinant of a d x d matrix and do a bunch of solves? That’s O(d^3) computation and O(d^2) storage.
I agree that the Beskos stuff hasn’t fine far enough (yet), but the fundamental problem will always be with that scaling. (MALA-type algorithms have it too)
The question ism when it takes a day to evaluate the likelihood (which is a small amount of time for big problems), is HMC still worth it.
I don’t know the answer. I’m defaulting to no, but given that the whole game is exploring the parameter space in as few likelihood evaluations as possible, it’s not crazy to think that it may be. (Hamiltonian flows aren’t magic, they’re just expensive, although (manifold) NUTS type adaptive schemes may help get the most bang from your buck)
Basically I’m circling around the standard objection to these methods: they’re too “hard-core” for methods that deterministic approximations will work on, while not being developed with genuinely hard things in sight (I mean, the multiple likelihood evaluations required for each sample would probably make me nervous about using it for a properly hard core infinite dimensional problem)
Also – anyone mentioning a grid in high dimensions probably (hopefully – then again I’ve seen people using Monte Carlo on 1d integrals…) isnt. Either it’s a sparse grid (in medium dims) or a randomised low discrepancy sequence. They work well. Although there’s not been a big breakthrough with quasi-MCMC methods, although there are certainly people trying! It’s an exciting time!!
“Don’t you need to compute the determinant of a d x d matrix and do a bunch of solves? That’s O(d^3) computation and O(d^2) storage.”
No, not at all. Euclidean HMC is O(d) storage and computation. Riemannian HMC is more expensive but also much more effective in terms of ESS/time, and that improvement actually gets better with increasing dimension. The scaling performance as demonstrated above isn’t that surprising when you understand the foundation of the algorithm.
“I agree that the Beskos stuff hasn’t fine far enough (yet), but the fundamental problem will always be with that scaling. (MALA-type algorithms have it too)”
HMC and MALA-type algorithms are completely different. HMC does not explore with random walks, which is why is scales with dimension.
“The question ism when it takes a day to evaluate the likelihood (which is a small amount of time for big problems), is HMC still worth it.
I don’t know the answer. I’m defaulting to no, but given that the whole game is exploring the parameter space in as few likelihood evaluations as possible, it’s not crazy to think that it may be. (Hamiltonian flows aren’t magic, they’re just expensive, although (manifold) NUTS type adaptive schemes may help get the most bang from your buck)”
Yes, yes it is worth it. That becomes clear when you start looking at the necessities for scalable algorithms (coherent exploration) and the possible implementations of coherent exploration (there’s HMC and… well, nothing). Hamiltonian flow is indeed the magic that makes that coherent exploration, and hence scalability, possible (it’s geometry on geometry on geometry for that triple layered mathemagic)
“Basically I’m circling around the standard objection to these methods: they’re too “hard-core” for methods that deterministic approximations will work on, while not being developed with genuinely hard things in sight (I mean, the multiple likelihood evaluations required for each sample would probably make me nervous about using it for a properly hard core infinite dimensional problem)”
Just because algorithms run for a few iterations doesn’t mean they’re using that computing time effectively. The accuracy of deterministic algorithms falls apart in high dimensions (nothing behaves as expected up there) and it’s extremely easy to mislead yourself with an “easy” answer. It’s a bit oxymoronic to claim that the most “hard-core” problems don’t need the most “hard-core” algorithms.
I’d love to see this write-up, especially if it includes hardware specs and timings.
I think Bob ran the models on his laptop, a 16 gig, quad-core MacBook Pro or there abouts.
At 10E6 ratings is Seconds/Sample for 1000 items actually lower (faster) than that for 100 items?
So you see a speedup on scaling? Am I making a blunder? When you throw more items at Stan, every sample becomes faster?
Dan and Mike: Great discussion!
Mike: I’ve used importance sampling successfully for logistic-GP with 900 dimensional latent space (you probably say that it is not a high-dimensional case). HMC mixes very slowly in this case. I’ll email you more details in couple days and you probably can tell why.