Paul Alper writes:
You recently posted my moving and widening the goalposts contention. In it, I mentioned “how diagnoses increase markedly while deaths are flatlined” indicating that we are being overdiagnosed and overtreated. Above are 5 frightening graphs which illustrate the phenomenon.
Defenders of the system might (ludicrously) contend that it is precisely the aggressive medical care that is responsible for keeping the cancers under control.
The prostate cancer graph is particularly interesting because it shows the peaking of the PSA-driven cause of treatment in the 1990s which then falls off as the evidence accumulates that the PSA was far from a perfect indicator. In contrast is the thyroid cancer which zooms skyward even as the death rate is absolutely (dead) flat.
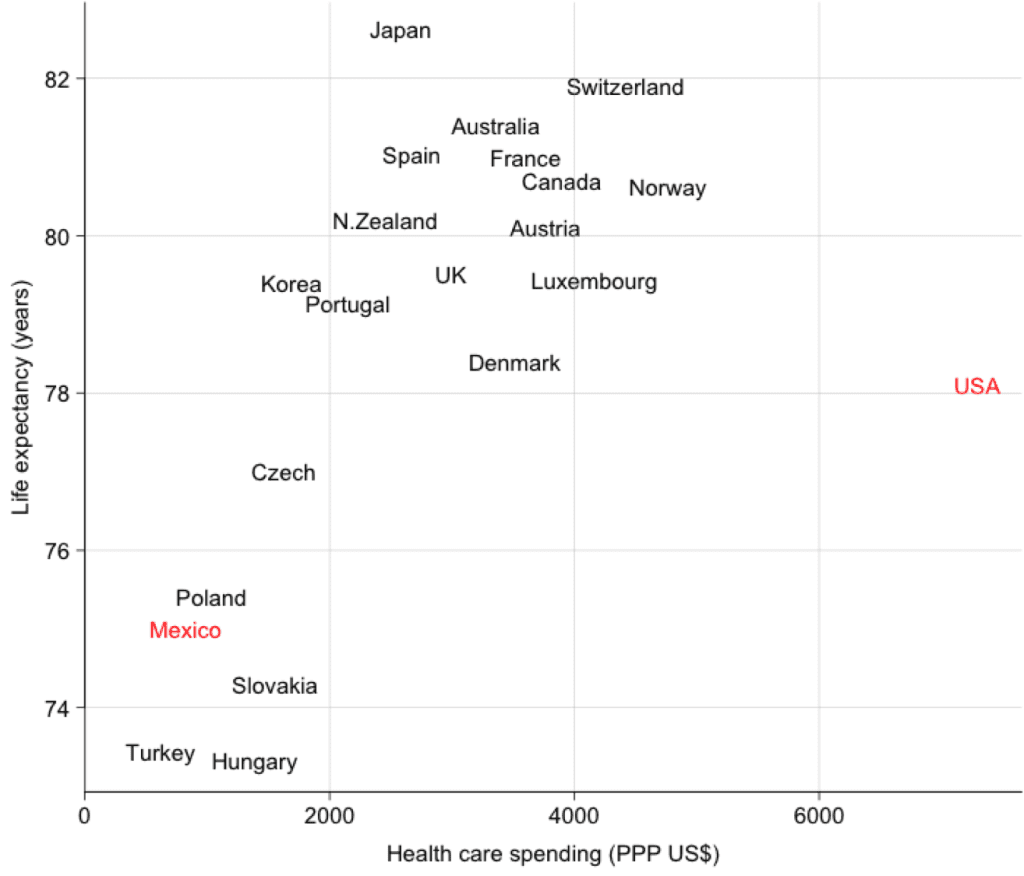
And of course here’s the famous cross-country comparison that some find “schlocky” but which I (and many others) find compelling:
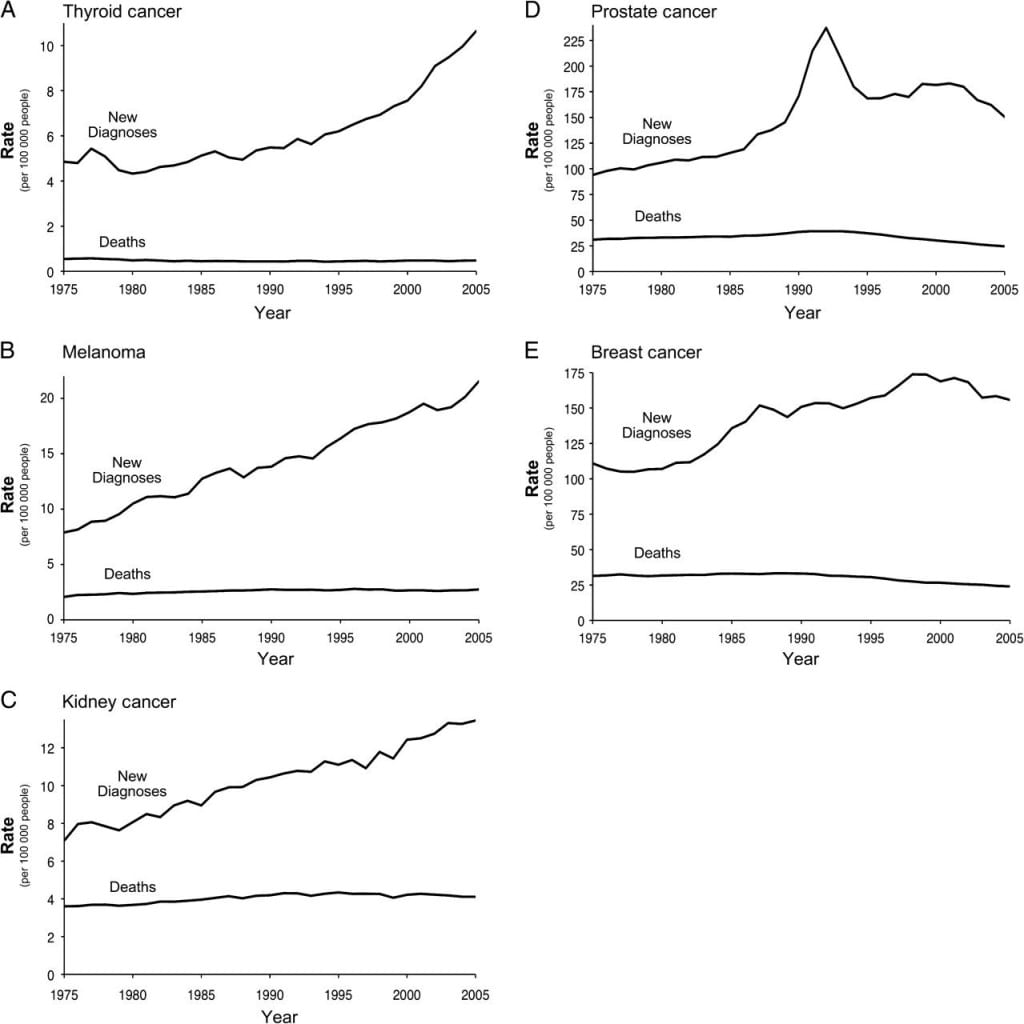
I do find the graphs to be very compelling evidence that early diagnosis has not had much effect on overall survival for these 5 cancers, but couldn’t the following two explanations also play a role in the results in the graphs?
(1) Reporting bias. The ability to report that a death is related to a particular cancer is a function of the ability to diagnose the cancer, so at least some fraction of the deaths that are reported in the figures would not have been counted without the increase in diagnoses. If this fraction is similar in size to the fraction of people saved by early diagnosis we would get basically the results as reported even though lives had in fact been saved that wouldn’t have been otherwise. There’s evidence in the prostate graph that increasing the number of diagnoses also increases the number of prostate cancer related deaths reported.
(2) Total incidence. The actual incidence of the disease in the population is actually much, much higher than the incidence of diagnosed disease, so in order to truly make a dent in the cancer-related deaths, the number of early diagnoses would have to increase by orders of magnitude compared to current levels.
What might make the argument more compelling is if there was a figure that showed no difference in survival between early and late diagnoses.
Isn’t is possible that the deaths have flatlined because we were doing a crappy job in the past identifying deaths due to, say, thyroid cancer in the first place? One evidence of this might be if the total mortality of all cancers together is falling? Is it?
Also, apart from death rates, for something like cancer, isn’t the months of additional survival a metric many patients find important?
With regard to prostate cancer, the mortality rate for the UK, where virtually no screening is done, is identical to that of the US where screening is widely practiced. “Months of additional survival” in the US is mainly due to lead time bias; that is, in the US, prostate cancer is detected earlier due to the screening but the patient dies at the same time in each country.
Note that each of the 5 graphs is taken from an article by Welch and Black in the April 22, 2010 issue of JNCI.
This post was admittedly put together too quickly without enough care.
http://statmodeling.stat.columbia.edu/2010/04/15/when_engineers/
But I think it does point to “things to consider when assessing evidence of the value of screening”?
Interesting: if I read these right, by eyeball, for 2005 that’s about:
1+25+3+25+4 = 58 deaths / 100,000 combined, round to 60.
and this claims 2005 population was 296M.
Our current population is about 315M, so assuming a similar death rate:
that’s 3150 X 60 = 189,000 … say 200,000 deaths ~ 2013.
Does that seem right? or is there something I’m missing?
For context, the 50th-anniversary Surgeon General full report says (p.41 of PDF):
‘Despite declines in the prevalence of current smoking, the annual burden of smoking-attributable mortality in the United States has remained above 400,000 for more than a decade and currently is estimated to be about 480,000, with millions more living with smoking-related diseases.’
So, I think that is ~480,000 compared to ~200,00, i.e., 2.4X larger, although of course there may be some double-counting, given that cigarettes may influence some of the cancers above.
Meanwhile, e-cigs offer great new marketing opportunities.
A few thoughts on the LE vs PPP graph:
1) Countries with comparable life expectancy spend 1/3 to 1/4 of what we do. Why are we spending so much?
2) What would happen if we cut back spending to $1800-2000 per person? Kinda looks like d(LE)/d(PPP) is on the order of 1 year per kilobuck for the rest of the world. What is it for the US? Is it similar or if we cut back to $2000k/person would we all start keeling over at 45?
3) Re #2, The Atlantic published a chart last Nov. which indicated that life expectancy pretty much saturates at 81 or 82 – http://www.theatlantic.com/business/archive/2013/11/the-singular-waste-of-americas-healthcare-system-in-1-remarkable-chart/281782/
On that chart the US looks like an even more extreme outlier than on the chart above.
4) Also re #2, it would be instructive to show LE vs PPP over time – just put up some points and connect the dots. That might allow one to infer d(LE)/d(PPP) – at least ballpark it.
I thought the causes of this had been pretty well explored years ago. The differences in the US on that chart are driven entirely by differences in GDP/capita (the US has very high GDP/capita) and accidental death’s (the US has a very high accidental death rate).
If you use a semilog specification of $/capita vs GDP/capita, the US is right where it should be. If you correct for the accidental death rate, the US is #1. See:
http://www.aei.org/files/2006/10/17/20061017_OhsfeldtSchneiderPresentation.pdf
Kevin:
Indeed, none of this is particularly new, at least not in general outline. In the U.S. we pay about twice as much as everybody else for healthcare without getting much out in terms of life expectancy. But it’s a big enough deal that it’s worth reposting on, from time to time.
I see Life expectancy as influenced by three important, somewhat orthogonal axes: genetics, heath-care-spending, & lifestyle-choices. e.g. I think USA spends a lot but our genes sabotage our attempts as opposed to say Japanese.
I wonder if there’s a way to deconvolute the effects. Maybe use something like hours-exercise-per-week as a surrogate for lifestyle-choice & life-expectancy 100 years ago as a weak surrogate for genetics?
Are there better ways?
That’s not particularly responsive to my point. I’m saying there is an old, well-known explanation for the effect, which you ignored when you raised the issue again. Given our accidental death rate and GDP/capita, the US gets pretty much the health care outcome it pays for compared to everyone else.
If you don’t agree, I would be very interested in hearing your explanation because presumably you are more familiar with both the statistical analysis and structure of the issue than I.
Kevin:
I’m no expert on health care policy; you may well know more about the topic than I do. My statement is based on the familiar piece of information, expressed in the graph above, that we in the U.S. spend twice as much per person as other countries on health care and don’t seem to get anything for it. Also my personal experience of U.S. health care as an expensive bureaucratic mess. Arguments that I’ve seen to explain this difference (such as the link you provided) haven’t persuaded me. You may be right, but I don’t see why we should be paying twice as much as other countries, just because our GDP is higher.
That said, I’m not saying that the new health care law is an improvement. I honestly have no idea, and it could well be that we are so screwed up at this point (with everyone from doctors to health care administrators demanding that their slice of the pie not be reduced) that there’s no easy way out. Which would be too bad. But, as noted above, I’ve not seen any data or analysis to dissuade me from agreeing with that the conventional wisdom that the U.S. system is a ridiculously expensive mess.
> there’s no easy way out
Perhaps, no affordable way out. Some have argued that Canada benefited from an historical accident that made it affordable many years ago.
Agree that fair comparisons between countries are rife with difficulties but the payments of twice the amount argue for the real difference to be positive _ir_regardless of those difficulties.
Some have argued that Canada benefited from an historical accident that made it affordable many years ago.
Tommy Douglas getting becomimg Premier?
I don’t see very many social science problems where there aren’t at least several variables that are important to an outcome. Trying to attribute causality in this case to the health care system in and of itself doesn’t seem very plausible.
Certainly, accidental deaths seem very relevant. Also, it seems possible that some healthcare expenditures are luxury consumption. We make them to make ourselves feel better psychologically–that something is being done. So GDP/capita could play some role. It doesn’t seem like it would be much work for a statistical wizard who does bioscience work to try a few different angles.
As far as a can tell, all large countries with diverse populations have messy health care systems
“Given our accidental death rate” Perhaps another indication that much of lifespan differences isn’t driven by what we’d consider medical care, but what we’d consider public health / engineering / politics, etc. I doubt the accidental death rate has much to do with medical care at all.
Where’s Italy? That has been for decades the leading/reference healthcare system in the G7…
And the link does not tell a story of “driven entirely” by GDP/capita, only “very” partially (see the outlier on page 8, the very fact that you need semilog for fitting means that it’s not explained away), and that “explanation” is further dispelled if you count in actual purchasing parity (and debt maybe too).
But anyway, comparing average GDP/capita in countries with vastly different Gini index is a bit of a joke altogether :-)
1. What does the scatterplot look like if we were to plot LE vs. pct GDP spent on health care? Would that pull the US into the LE>78 cluster?
2. Changes in per capita spending shouldn’t affect the accidental death rate. (Should they?) So if accidental death rate is limiting LE in the US then we’d expect d(LE)/d(PPP) = 0, no?
3. Inspired by the AEI charts: How about breaking LE down by age group? Create plots for newborns, 15-year-olds, 45-year-olds, and 65-year-olds. Are we spending 3-4x per capita for all age groups?
4. Question on the AEI charts: I’m not clear on the “moral hazard” associated with Single Payer. (Item #6 in the “Disadvantages” column on chart #29) Would Single Payer create a market incentive to contract meningitis? Pancreatic cancer?
Regarding question 4: In the context of health economics, the ‘moral hazard’ of concern is that people might seek care that they don’t really need, if the care is provided at less than market price. This is probably a reasonable concern if we are talking about too much medical testing. Note that there are similar incentives for medical providers (to provide too many services), though that is usually called provider-induced demand.
Having said that, I am not sure why moral hazard is listed as a characteristic of single-payer systems — it arises whenever there is a third-party payer, and is just as much a concern with US-style health insurance (this is why we have co-pays etc).
I was being a little flip with #4. “Meningitis? Pancreatic cancer? Tough it out. No running up frivolous expenses and leaving us hardworking taxpayers on the hook for them.” I’m not seeing the moral hazard angle there. (FWIW, I do recall reading about the RAND Health Insurance experiment – http://www.rand.org/health/projects/hie.html)
And what on earth is the rationale for using the semi-log here? Because R-squared goes up? But R-squared goes up just because that specification allows you to bend the curve to meet the single extreme outlier, the USA. Really reaching for it.
The US is “right where it should be” because the USA data makes a highly influential point – any model that included the USA data would predict the USA data.
If you leave out the USA data and fit the same type of model as in the paper (semilog) then the residual for the USA is about the same as that for a linear model.
In R and using the 2010 data from
http://stats.oecd.org/index.aspx?DataSetCode=HEALTH_STAT
(excluding Turkey – no data, Norway and Luxemborg because they are also extreme and were obviously left out in the paper as well)
(and fingers crossed that it comes out right)
health <-
structure(c(8.9481, 11.0318, 10.503, 11.3738, 7.37, 7.4319, 11.0751,
6.3394, 8.9888, 11.677, 11.5495, 9.5277, 8.0302, 9.2925, 9.312,
7.6856, 9.4079, 9.589, 7.2911, 7.1675, 6.1782, 12.0661, 10.1995,
9.4224, 7.0229, 10.797, 8.995, 8.8718, 9.6074, 9.4688, 10.8817,
9.5504, 17.6911, 41644.96367, 40535.20542, 38273.38497, 38916.87169,
18295.23322, 25834.52081, 40926.76878, 20470.32305, 36585.82999,
34894.43606, 38319.81724, 27998.6651, 21134.83749, 36637.25671,
41131.07786, 26868.87546, 32887.37779, 33759.51744, 28210.09674,
83973.5354, 15725.83914, 41587.33494, 30246.27032, 57742.01727,
20207.99905, 25713.08046, 23789.65085, 27004.2188, 31640.14371,
39567.04326, 48733.4048, 34524.37735, 48287.47224), .Dim = c(33L,
2L))
countries <-
c("Australia", "Austria", "Belgium", "Canada", "Chile", "Czech Republic","Denmark",
"Estonia", "Finland", "France", "Germany", "Greece","Hungary", "Iceland", "Ireland",
"Israel", "Italy", "Japan","Korea", "Luxembourg", "Mexico", "Netherlands", "New Zealand",
"Norway", "Poland", "Portugal", "Slovak Republic", "Slovenia", "Spain", "Sweden",
"Switzerland", "United Kingdom", "United States")
plot(health[,2],health[,1],pch=15,xlim=c(10000,90000))
text(health[,2],health[,1],paste(" ",countries,sep=""),adj=0)
a<-lm(log(health[-c(20,24,32),1])~health[-c(20,24,32),2])
x<-10000:80000
lines(x,exp(a$coefficients[1]+x*a$coefficients[2]),col=2)
b<-lm(health[-c(20,24,32),1]~health[-c(20,24,32),2])
lines(x,b$coefficients[1]+x*b$coefficients[2],col=3)
The difference between US spending per capita and the rest of the world is driven by 3 factors: we pay higher prices per unit of service; we get more of the most expensive kinds of care (e.g. specialist visits, cardiac stents); and we undergo much more rescue care in the last few months of life (e.g. days in the ICU). And yet, we have worse life expectancy, worse infant mortality, worse maternal mortality, worse outcomes for many specific diseases. Part of our poor showing in the health statistics is due to higher rates of homicide and car accidents, but it is also due to infant mortality and higher rates of poverty compared to peer nations (western Europe, Canada, Japan, Australia/NZ). In other words, we spend more on the most expensive kinds of healthcare, less on social services, and get worse health.
While the contention might be true….
(1) Why does it all need to be true? I don’t think it is too shocking to claim that PSA screening is of limited benefit, but I don’t see why we need a single story for all screening. I anticipate the magnitude of the benefits probably ranges quite widely.
(2) I can’t see how these comparisons show anything causal. I buy that there may be (is probably?) overdiagnosis of cancer, given the various incentives at play, but this info does not shift my prior.
Mortality rates decline roughly exponentially over time. Replot in logarithmic scale to see what’s happening.
I am not sure what this graphs (the first series) are supposed to demonstrate. (Sorry, it might be very naive). People do eventually die from one cause or another. And if someone has cancer, chances are they will die from that cancer. So the true criterion is added survival time with early diagnosis or improved quality of life during treatment. Quality of life is hard to measure, but survival times after diagnosis have to be available (sure, one needs to reweigh to make the same stage mix and comparable demographics).
A much-quoted metric is 5-year survival rate. It is also a very poor metric because, as it has been noted many times, it is a bad surrogate for what we really wish to know: mortality. Thus, the United States, unlike other developed nations, has great 5-year survival rates because we busily screen either for diseases for which we have ineffective treatments or for diseases which are “incidentalomas” (incidental tumors which are often benign or unlikely to cause problems). Many cancers are not fatal and incidentalomas often lead to unnecessary testing and treatments which are harmful. Welch and Black discuss this at length in their JNCI article.
I don’t see how you can dismiss 5-year survival rates so easily. Lead time bias may be one explanation yes. But how can we be certain? Say early screening, detection & treatment does indeed prolong survival by, say, 7 years. Then too, mortality will remain unchanged but isn’t the gain in additional years a outcome people care about?
Do you have data that indeed shows that the patient dies at the same time in each country, screening or not?
The following is an excerpt from Gerd Gigerenzer’s article, “Five year survival rates can mislead”:
While running for president of the United States the former New York mayor Rudy Giuliani announced in a 2007 campaign advertisement, “I had prostate cancer, 5, 6 years ago. My chance of surviving prostate cancer—and thank God, I was cured of it—in the United States? Eighty-two percent. My chance of surviving prostate cancer in England? Only 44 percent under socialized medicine.”
To Giuliani this meant that he was lucky to be living in New York and not in York, because his chances of surviving prostate cancer seemed to be twice as high in New York. Yet despite this impressive difference in the five year survival rate, the mortality rate was about the same in the US and the UK.
Why is an increase in survival from 44% to 82% not evidence that screening saves lives? For two reasons. The first is lead time bias. Earlier detection implies that the time of diagnosis is earlier; this alone leads to higher survival at five years even when patients do not live any longer. The second is overdiagnosis. Screening detects abnormalities that meet the pathological definition of cancer but that will never progress to cause symptoms or death (non-progressive or slow growing cancers). The higher the number of overdiagnosed patients, the higher the survival rate. In the US a larger proportion of men are screened by prostate specific antigen testing than in the UK, contributing to the US’s higher survival rate.
…journal editors and reviewers should no longer allow misleading statistics such as five year survival to be reported as evidence for screening.
The excerpt explains how five year survival rates can mislead, but does not provide exceptional proof that it does mislead.
A greater effort needs to be made to deconvolute mortality and five-year survival. Five year mortality mortality and ten year mortality are both mortality, but if I’m going to die from the cancer, having an extra five years would mean an awful lot to me. But even so, the phrase “the mortality rate was about the same” which is a tacit admission that it is, in fact, lower in the US.
As for lead time bias and overdiagnosis, all that’s given is an explanation of how it might account the large difference, but we still need evidence that it does account for all of the difference before we can just dismiss five-year mortality as you apparently have.
One thing that might shed some needed light is a way of estimating at the time of first diagnosis how long a person has had the cancer. This might not be easy given that people will begin being treated soon after diagnosis so having untouched biomarkers to be able to make that estimate might not happen very frequently. The good news is that it might happen more frequently if enough people take to heart the message of the book and refuse treatment after diagnosis.
We may never know if what you call overdiagnosis is in fact overdiagnosis, but it does seem like the problem itself may have been overdiagnosed. I’d like to know if we’re wasting time and money and decreasing people’s quality of life by overdiagnosing disease, but that becomes less possible if we rush to dismiss a metric that is meaningful to those suffering from cancer because a theory says that overdiagnosis and lead time bias might account for all the difference between five year survival between countries with differing levels of screening, even though the question of whether or not it does has not been fully explored.
Again, what you are showing is that “Five year survival rates can mislead” but not “Five year survival rates do mislead”
We need to know how much of the survival rate improvement is due to lead time bias & how much due to real pushing the mortality forward.
Isn’t there a potentially simpler and less scary explanation for the first set of graphs? Those are graphs of the inflows and outflows (people per unit time) of a stock (people with a particular disease). The stock (state variable, accumulation) decouples the two flows.
What if you assume both graphs are true as shown, ignoring any better or more aggressive diagnostics for a moment? That means the net inflow is the difference of the two graphs. Roughly, that means the net inflow is the upper graph offset by a constant.
/That/ implies that the stock (number of ill people) must be growing. That’s possible if the flow out of the stock is not proportional to the stock (i.e., not a 1st-order decay), which seems to imply that survival times are increasing. That’s potential good news!
Of course, some increased diagnostic ability may be happening, too, but I see this as a potential key message. How might you test for that?
Paul may have mentioned that in his article. While I really want to, I don’t have time to read it right now.
The stock is of “people diagnosed with cancer X”, note that this stock is increasing. most likely the stock of “people who have undiagnosed cancer X” is decreasing. Increase the diagnosis rate because you increase testing while keeping the outflow (mortality) rate constant, and you get the result shown.
I think the concern is something along the lines of “we aren’t really lengthening people’s lives, but we sure are increasing the number of years that patients suffer unpleasant aggressive treatments, and buying a lot of fancy luxury goods for Oncologists….”
Daniel, I agree that this stock is increasing and that you’ve got the name (or description) right. I also agree with the other stock you identified.
We can test that theory of overdiagnosis without cure, though. I’ll do a mental experiment, but it wouldn’t take much longer to write and simulate the differential (or integral) equations to get more confidence in the answer.
Let’s assume that the world (or country) population is constant and that the incidence of new disease per year is constant. We’ve seen the deaths per year is constant, too, in the graphs.
Increasing the diagnosis rate (e.g., the fraction undiagnosed who are properly diagnosed per year) moves people from the undiagnosed stock to the diagnosed stock. If that fraction goes from a low, original level (say, 0.2) to a new, higher level (say, 0.6) and stays there, then the population of ill people will redistribute itself until the ratio of the two stocks is inversely proportional to the fractions that clear each stock per year, right (at least approximately)?
Since the fraction diagnosed per year has an upper limit of 1 and perhaps something lower than 1, we should likely reach or approach such a stable point at some time.
If that’s true, then the number diagnosed per year will decline back to the original level after the redistribution is complete. That’s something we can look for; if it’s diagnosis without cure, the apparent growth in new cases (really the growth in new diagnoses) will peak and return to the incidence of new cancers.
If it doesn’t return to the original, is that a sign that something else–perhaps a lengthened survival period–is at play?
This mental model is pretty simple. The population is growing, deaths happen from both stocks, and cures (or remissions) happen from the ill stock (at least for some cancers). Those things and others could be easily added to a model and tested for reasonableness.
Does that make sense? Is the reasoning reasonable?
With all your caveats, yes. I think the big point is these are (pseudo) differential equations (technically the number of people in any stock is always an integer, but we can call 1 person “infinitesimal” as a fraction of the population in the year 2000, and deal with “fraction of the number of people in the population in the year 2000” as our state variables…)
On the other hand, it seems that the timescale of relevance would be longer than 30 years, based on the dynamics I’m seeing above they might be well longer than 30 years, like maybe 150 before we reach a pseudo-steady state… so it’s worth addressing the question by probing more concertedly than just looking for a return to a steady state after a transient. Also, we keep inventing new screening methods and changing our recommended policies and things. So the forcing function is not in steady state either.
The big concern everyone has is that if the mortality rate isn’t going down, then either we’re increasing the conversion rate of new cancers at exactly the rate that balances the improvements in our treatment, or if the conversion rate isn’t changing, we’re not lengthening lives.
Specifically let’s write the following model structure:
Diagnosed population
General Population —–>acquire cancer —–> diseased population { } —> cancer death
Undiagnosed population
If the rate of cancer death is constant we can get that because we have constant acquisition rate and constant life expectancy…. or we can get that because we have dynamic acquisition rate, and dynamic changes in life expectancy that JUST HAPPEN TO CANCEL OUT.
The JUST HAPPEN TO CANCEL OUT is just a little TOO unlikely to be taken at face value…
Ack, the blog stripped out all my whitespace that made the little ASCII diagram make sense… Basically the diagnosed population and the undiagnosed population together make up the diseased population… and the dynamics between those two don’t affect the stock of total diseased population.
This assumes that the new diagnosis rate is constant. Perhaps, because we are constantly pushing for better and better ability to diagnose, the diagnosis rate is steadily increasing so we may not regress to the original until some time after the rate of diagnosis plateaus. Everything else makes sense.
Your statement is refreshingly quite strong:
“we aren’t really lengthening people’s lives, but we sure are increasing the number of years that patients suffer unpleasant aggressive treatments, and buying a lot of fancy luxury goods for Oncologists….” And, I am glad that it is you who are making it rather than me because I have had a great deal of opposition among friends and relatives who absolutely believe that screening is an unadulterated positive aspect of medicine, devoid of harm or profit.
However, according to the NYT recent article on the 25-year breast cancer study, there are 37 million mammograms done per year at about $100 each, yet the RCT study concludes:
“Annual mammography in women aged 40-59 does not
reduce mortality from breast cancer beyond that of physical examination
or usual care when adjuvant therapy for breast cancer is freely available.
Overall, 22% (106/484) of screen detected invasive breast cancers were
over-diagnosed, representing one over-diagnosed breast cancer for
every 424 women who received mammography screening in the trial.”
Be sure to look at Figs 2, 3, and 4 for overwhelming evidence that mammography (the treatment) had no medical advantage for the patient compared to the control.
PBS Frontline show from a few years back: “Sick Around the World: Can the U.S. learn anything from the rest of the world about how to run a health care system?”
Link = http://www.pbs.org/wgbh/pages/frontline/sickaroundtheworld/
I’d love to know the changes in diagnosis by age — crude numbers may reflect population aging as much as overdiagnosis.