Joshua Vogelstein pointed me to this post by Michael Nielsen on how to teach Simpson’s paradox.
I don’t know if Nielsen (and others) are aware that people have developed some snappy graphical methods for displaying Simpson’s paradox (and, more generally, aggregation issues). We do some this in our Red State Blue State book, but before that was the BK plot, named by Howard Wainer after a 2001 paper by Stuart Baker and Barnett Kramer, although in apparently appeared earlier in a 1987 paper by Jeon, Chung, and Bae, and doubtless was made by various other people before then.
Here’s Wainer’s graphical explication from 2002 (adapted from Baker and Kramer’s 2001 paper):
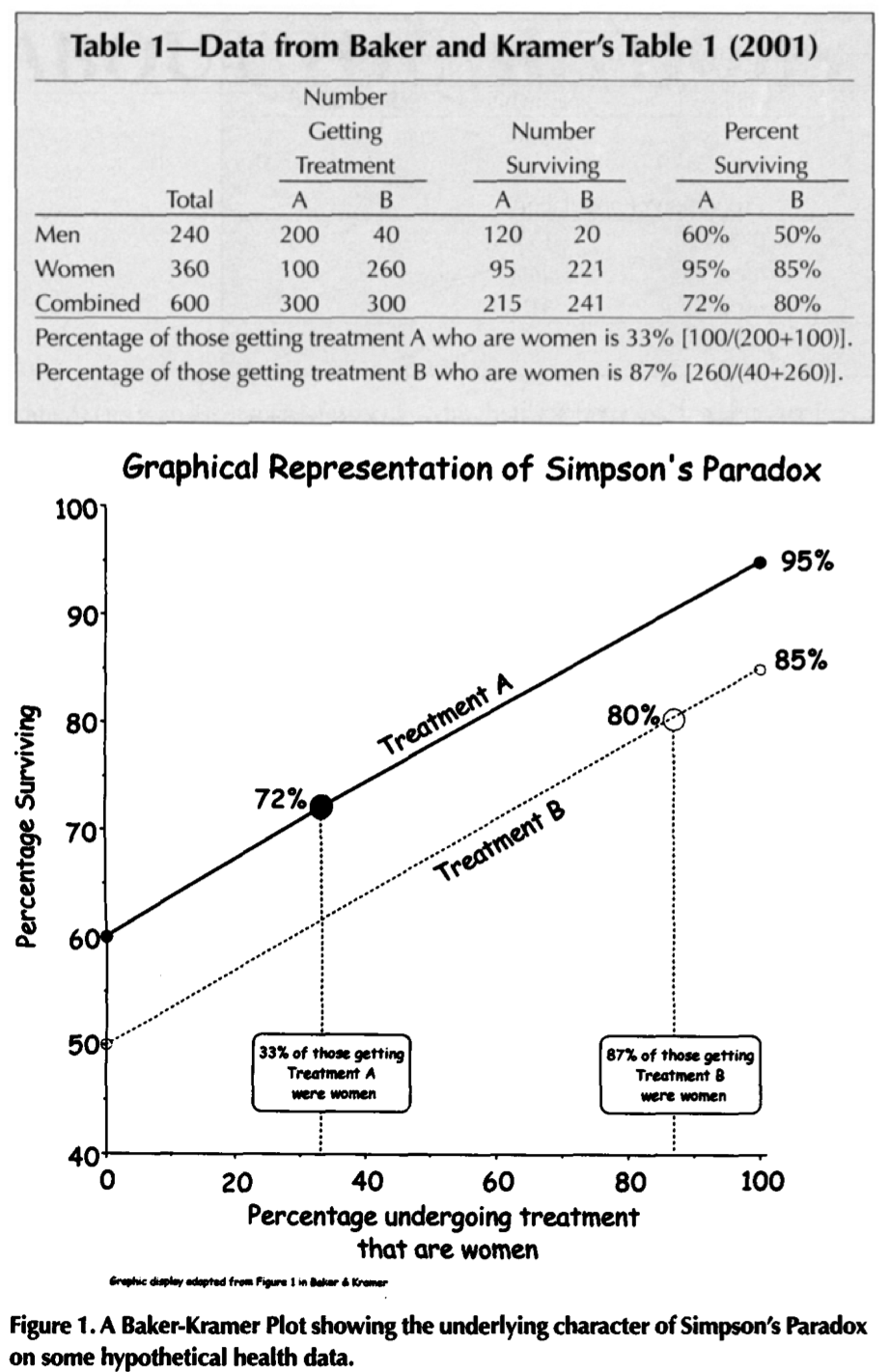
Here’s the version from our 2007 article (with Boris Shor, Joe Bafumi, and David Park):

But I recommend Wainer’s article (linked to above) as the first thing to read on the topic of presenting aggregation paradoxes in a clear and grabby way.
P.S. Robert Long writes in:
I noticed your post about Simpson’s paradox and wanted to let you know about another nice teaching approach using DAGs based on a paper by Perl, but implemented in the fantastic DAGitty tool:
http://dagitty.net/learn/simpson/I have used this to teach Simpson’s Paradox to masters level students recently. The module (led by Mark Gilthorpe) teaches advanced modelling concepts.
The DAGitty tool simulates the data which you can give to the students and ask them to explore. You have a main exposure X and outcome Y, and various “potential confunders” Z1, Z2 etc. The beauty of this is that by running models that successively add more of the potential confounders, the estimate for the main exposure X changes from positive to negative and back again.
Y~X+Z1 gives a correct estimate
but
Y~X+Z1+Z2 gives a biased estimate
and
Y~X+Z1+Z2+Z3 gives the correct estimate
and so on.So the students get very confused by that. So then you show them the DAG and it all nicely falls into place, with the bottom line of “be careful what variables you thrown into a model.”
I have mixed feelings about this particular tool as I often work in settings where the concept of “true causal effect” doesn’t mean much. On the other hand, causal reasoning is often a central goal for researchers, in which case this tool could be helpful.
P.P.S. Let me clarify the above point about causal inference as it seems to have led to a lot of confusion in the comments:
There are examples of conditioning paradoxes in which causal reasoning does not arise. Red-blue is an example. There’s no treatment involved at all, I’m just looking at different sorts of comparisons in the data. Comparisons can be interesting and important even without a causal question. I’m not dismissing the importance of causal inference (obviously not; look at the title of this blog!), I’m just saying that puzzles of conditioning arise even in non-causal settings, which suggests to me that causal reasoning is not necessary for the understanding of these problems, even though in many settings it can be useful.
A helpful analogy here might be to statistics and decision analysis. Statistics is sometimes called the science of decisions, and statistical inference is sometimes framed as a decision problem. I often find this helpful (hence the inclusion of a decision analysis chapter in BDA) but I also have seen many examples of statistical analyses where there is no corresponding decision, where the goal is to learn rather than to decide. Hence, although I often find decision analysis to be useful, I don’t feel that it is a necessary part of the formulation of a statistical problem. My attitude toward causal reasoning is similar.
One of my personal favorite ways to show this is using ellipses (although I admit that isn’t suited for many audiences). See Figure 7 of Elliptical Insights: Understanding Statistical Methods through Elliptical Geometry (Friendly, Monette & Fox, 2013) http://arxiv.org/pdf/1302.4881.pdf
For the aggregation bias plot a slight variant I have used in presentations is to use panels. In the left hand panel have the individual level data using smaller point markers & the individual level (within group) regression lines. Then in the right panel use larger point markers and the regression line with the aggregate data. Having in separate panels makes it easier to keep it straight which line corresponds to which regression, as even with only 3 or 4 lines the graphic can become confusing and overplotted.
Here I trudged up that example I was talking about, see https://dl.dropboxusercontent.com/s/9yfm4fag5jsnn83/Chart1.png (which was just simulated data to illustrate the point – not actual data).
Not sure how apt this is, but personally I love this graph:
http://upload.wikimedia.org/wikipedia/commons/4/47/Simpson%27s_paradox_continuous.svg
I’d like to second that.
Most clear and simple depiction of the reversal phenomena that I found in all the examples given here.
Wainger’ links are dead (currently?)
I had gotten my hopes up thinking I would see a DAG (PDF) showing this is an extremely simple problem of confounding. My hopes were dashed. This is fundamentally a causal, not an aggregation, problem.
Armed with a hammer everything looks temptingly like a nail? :)
@Rahul:
I imagine you are referring to statisticians ;-)
They are the ones hammering at the problem when all you need is pencil, paper, and a willingness to draw like a toddler.
Fernando:
I just see that as one _story_ of what’s paradoxical.
I think its just an instance of the more general story of what you see/think in N-1 dimensions can be totally undone in N dimensions.
Here Simpson’s refer to Homer in that episode were he inadvertently encounter 3 dimensions.
K?
From where I stand I don’t see anything paradoxical.
The “paradox” is a result of misspecification and, more deeply, of a statistical language that is riddled with ambiguity when dealing with causal questions.
Like one if those M C Escher drawings an ambiguous language condemns us to ever going round in circles.
Language and symbols are fundamental to scientific progress. Unfortunately they are also subject to identity politics.
Fernando:
I don’t find Simpson’s paradox or the red-blue story paradoxical. Indeed, Rubin once said that there is no such thing as a paradox in the sense that, once you understand it, the paradox has been resolved. Simpson and red-blue might be better described as “puzzles,” in the sense of the way that word is used in social science. A puzzle is a stylized fact that seems to contradict how we understand the world. But through a deeper formulation, the puzzle is resolved. It is still a puzzle in the same way that a jigsaw puzzle is still a puzzle after all its pieces have been put into place; it is just then a solved puzzle.
In any case, I find the B-K plot and the red-blue plot to be helpful in resolving the mathematical puzzle of aggregation and conditioning. If you prefer, you could think of these graphs as mnemonics that are helpful to me, in the same way that various diagrams have been constructed over the years to make the Pythagorean theorem feel more intuitive.
Andrew:
We fundamentally agree but I’d like to push a little further.
The graphs above are representations of data, and those are useful. Indeed to some people they are the most useful.
But a DAG is something different. It is a _mathematical object_ capturing – in one picture – the hypothesized underlying system of non-parametric structural equations generating the data. As a generative model it goes directly to the source of the problem. It is the directness of the formalism that makes it so powerful.
Fenando,
You are the only one on this blog who addressed the REAL PUZZLE.
DAGs convey causal information, all the other representation just
replicate the tables in different lights.
But people are reluctant to use causal vocabulary –comfort zone – human nature.
It took one hundred years before people began talking in
calculus vocabulary, and you would think the process should be faster
in the age of internet — wrong.
I’m comfortable with the idea of causality, partially because I come to this with a bit of a background in system dynamics, which is all about causal issues–finding them and possibly changing them to achieve different ends.
I’m curious: why a just a DAG? Much of causality that I see through my lens is circular. For simple examples, people cause births, and births cause people, or money in a bank account causes interest to be paid, and interest causes money in a bank account to increase. What about a DG / digraph?
Bill Harris,
You are absolutely right.
The theory of counterfactuals works for cyclic graphs too,
and d-separation works in linear cyclic graphs.
DAGs are the first step toward operationalizing this theory
in policy analysis. But there is a lot of fertile land for
extending causal analysis to cyclic models. Please join.
Andrew,
This time we are in agreement. Yes, Simpson’s paradox is a puzzle, not a paradox.
But, have we solved the puzzle?
The puzzle is not why conditional associations are different than marginal associations,
this is what the tables show, and regression equations show, and the B-K plot show,
and dozen of other representations show, and this is what you and so many on this blog
consider to be “once you understand it, the paradox is resolved”. No way! This resolves
a non-puzzle, while the real puzzle remains unresolved, not even addressed, mostly avoided.
So, here is the real puzzle:
How come famous statisticians (etc. Simpson, Lindley) reach consensus on what the
correct action is in each context, and change their opinion when the context changes
while the data remains the same. In other words, in context-1, all statisticians
agree that the correct thing to do is to consult the aggregated table and,
with the same data, but in context-2, all agree that the correct thing to do
is to consult the disaggregated data .
In still other words, you understand how association can reverse sign by aggregation
Great!. But you avoid the real puzzle, to determine which sign is the “sensible one”
(Simpson’s words) in context-k, and what is it about a “context-k” that makes us (and hundreds of smart statisticians” change opinion in consensus.
(This consensus, btw, happens to coincide with the “true causal effect” . But since you
say that you do not believe in “true causal effect”, I replaced it with consensus, which is an observed undisputed phenomenon.)
A resolution of this dilemma is offerred here:
http://ftp.cs.ucla.edu/pub/stat_ser/r414-reprint.pdf
Do you have another solution? Do you think the B-K plot offers a solution to
THIS DILEMMA? Obviously it does not, because it does not contain more information
than the tables themselves. So in what sense do B-K plots, or ellipsoids, or vectors
display, or regressions etc. contribute to the puzzle?
They dont. They can’t. Why bring them up?
Would anyone address the real puzzle?
The nice thing about Simpson’s paradox is that it does not allow statisticians
to get off the hook with hand waving. It is a puzzle that cannot be resolved
in the language of traditional statistics, but requires causal vocabulary,
No escape. Those who honestly address the puzzle (about the consensus) must enrich
their language with DAGs or potential outcomes (or SEM), and those who refuse such
enrichment, are simply admitting disinterest in the real puzzle, and will continue to
bring up plots, ellipsoids and regression equations and all kind of statistical
representations from their comfort zone, and make believe they “understand Simpson’s
paradox”.
This means that Simpson’s paradox will be with us for the next one hundred years.
If casual analysis is indeed an objective in instruction, students need grounding in philosophy to better evaluate whether “modern” methods of causal analysis are really so novel or useful. “Prime mover” anyone?
jsb,
Modern methods of causal analysis may not be “novel”
since the roots of everything can be gounded in Aristotle and Genesis.
There is only one pleasing thing about modern methods that you could
not find in Aristotle and Genesis: We can solve most problem that we wish
to solve in policy analysis, attribution, mediation, etc etc. including, no surprise, Simpson’s problem: Give me a story and data and I will
tell you which treatment should be recommended.
Andrew,
You write:
“I find the B-K plot and the red-blue plot to be helpful in resolving the mathematical puzzle of aggregation and conditioning.”
If so, do these plots help us resolve the decision problem too? Namely
which treatment is more effective? The one that appears more effective in the
disaggregated tables, or the one that appears effective in the aggregated table?
Or is this not part of the puzzle?
In 1981, Lindley and Novick asked this question, and declared it to be the
essence of Simpson’s paradox. We are now more than 30 years wiser.
What do the B-K plot and the red-blue plot helpful in resolving?
Do you agree with me that they not helpful at all in resolving Lindley’s
interpretation of the puzzle?
Judea:
You write, “Do you think the B-K plot offers a solution to THIS DILEMMA? Obviously it does not, because it does not contain more information than the tables themselves. So in what sense do B-K plots, or ellipsoids, or vectors display, or regressions etc. contribute to the puzzle? They don’t. They can’t. Why bring them up?” And you write, “do these plots help us resolve the decision problem too?”
My response is that there is a mathematical challenge which does not involve any decisions, as can be seen in the red-blue example. People have difficulty holding in their head that an aggregate pattern can go in the opposite direction as an individual pattern, and I think graphs can help here. I like graphs in all sorts of settings. To say that a graph “does not contain more information than the tables” is somewhat misleading in that the purpose of the graph is not just to contain information but also to engage the reader’s brain. I am a visual creature and graphs help me a lot. People differ in this regard, but for me (and for Howard Wainer, and for the millions of people who’ve bought Ed Tufte’s books and who click on infographics every day), graphs are helpful.
Finally, I’m not saying that you should stop doing what you’re doing. There are lots of difficult statistical problems out there. If your methods can help people decide what medical treatment to take, that’s great. And I think that when Baker, Kramer, Wainer, and others (including myself) work on methods to help people understand patterns in data, that’s useful too.
Andrew,
I never insinuate that you object to what I am doing.
What I claimed is that you did not explain to me why comparing
groups with and without conditioning is “intriguing” (your word),
and what the purpose is of comparisons in your example of blue state
and red state.
If I watch a ball using red glasses and then using green glasses and
I find that the ball’s color changed, I am not surprised.
But if I watch a ball with my right eye, then with my left eye and
find that the color changed I ask WHY.
So, why are you surprised, in the red/blue state example, that an
association changed sign upon conditioning? Isn’t just a matter of
watching a ball with two different glasses?
BTW, I find the graph shown in wikipedia (Simpson paradox) right upper
corner to be the clearest visualiztion that associations can reverse
sign. This still leave us with the philosophical dilemma of why people
expect the sign to remain invariant, even in cases where (on the surface)
there are no treatments involved.
I think anyone who claims that the paradox (sorry, the puzzle) is resolved
by this or that representation, should first address the question of why
it is a puzzle.
Judea:
I am not surprised by the red-blue paradox but many people are. Just search this blog for Tucker Carlson, Michael Barone, David Brooks, Jonathan Haidt, David Runciman, and various others. The purely mathematical problem of conditioning and averaging is confusing to many people, hence the value of plots such as the B-K plot and ours. I also think the study of causal inference is valuable, it’s just that right here I am focusing on something else. Regarding the question of why people get so confused on this, we discussed this in our red-blue article and also in our book. I think part of the confusion has to do that leading U.S. journalists mostly live in certain parts of the country and not others.
Fernando:
> Like one if those M C Escher drawings
I see those as (attempts at) representations that no cognisant being can take to actually represent something.
(Think McCullagh did the same for statitiscal models e.g. Normal if sample size even, Cauchy if odd.)
Seeing why N-1 misleads given a view of N resolves the puzzle.
See the PS that Andrew just added to the blog.
Robert Long,
Your simulation module gets to the essence of Simpson’s paradox.
I hope you are not discouraged by Andrew’s remark, that:
“I have mixed feelings about this particular tool as I often work in settings where the concept of “true causal effect” doesn’t mean much.
Your simulation module proves that “true causal effect” exists, because one can run
a randmized controlled experiment on it, and actually measure the “true causal effect”.
Moreover, “the concept of true causal effect” actually exists in the mind of every statistician,
else we would be able to explain the consensus that statisticians form when asked
about “which treatment is better”?
Judea:
I agree completely that in the case of a treatment it makes sense to think in terms of causal inference. In other settings such as the red-blue problem there is no treatment; I am just trying to understand a pattern in the data and no causality is involved.
Andrew,
I dont buy it.
Why would innocent reversal of association evoke surprise and disbelief?
Why dont we just call it: “two ways of looking at data”.
You say: “I’m just looking at different sorts of comparisons in the data. Comparisons can be interesting and important even without a causal question.”
But why do we compare? We usually compare in order to say something about who is larger,
who is better, who is more faithful, etc. If we just compare for obtaining two
views of data, we should not be surprised if in one view an association is positive
and in another, it is negative. We only become surprised if the associations of interest
are expected to be invariant to the way we look at them. But we know that associations
change by conditioning, so why the surprise?
I claim that in every example in which the reversal appears to be “paradoxical”
or even “puzzling” there is a hidden “treatment” in the mind of the analyst. Sometimes
it is explicit and sometimes it lurks in hiding, or suppressed.
Here is my reasoning (taken from Am. Stat.)
In explaining the surprise, we must first distinguish between “Simpson’s reversal” and
“Simpson’s paradox”; the former being an arithmetic phenomenon
in the calculus of proportions, the latter a psychological
phenomenon that evokes surprise and disbelief.
A full understanding of Simpson’s paradox
should explain why an innocent arithmetic reversal of
an association, albeit uncommon,
came to be regarded as “paradoxical,” and why it has
captured the fascination of
statisticians, mathematicians and philosophers for over a century
(though it was first labeled “paradox” by \citet{blyth:72}). %%Blyth (1972)) .
The arithmetics of proportions has its share of
peculiarities, no doubt, but these tend to
become objects of curiosity once they have been demonstrated
and explained away by examples.
For instance, naive students of probability may expect
the average of a product to equal the product
of the averages but quickly learn to guard against such
expectations, given a few counterexamples. Likewise,
students expect an association measured
in a mixture distribution to equal a weighted average
of the individual associations. They are surprised, therefore,
when ratios of sums, $(a+b)/(c+d)$, are found to be ordered differently
than individual ratios, $a/c$ and $b/d$.\footnote{In Simpson’s paradox we witness the
simultaneous orderings: $(a1+b1)/(c1+d1)> (a2+b2)/(c2+d2)$,
$(a1/c1)< (a2/c2)$, and $(b1/d1)< (b2/d2)$.}
Again, such arithmetic peculiarities are quickly
accommodated by seasoned students as reminders
against simplistic reasoning.
In contrast, an arithmetic peculiarity becomes “paradoxical'' when it clashes with
deeply held convictions that the pecularity is impossible,
and this occurs when one takes seriously the
causal implications of Simpson's reversal in decision-making contexts. Reversals are indeed impossible
whenever the third variable, say age or gender, stands for a
pre-treatment covariate because, so the reasoning goes,
no drug can be harmful to both males and
females yet beneficial to the population as a whole.
The universality of this intuition reflects
a deeply held and valid conviction that such a drug
is physically impossible. %%insert-6
Judea:
I agree with you that conditioning can be tricky and interesting in settings where causation is involved. It can also be tricky and interesting in settings such as red state blue state where causal questions are not involved.
See my P.P.S. in the above post. Causation is important but it does not arise in all problems. Just as decision analysis is important but does not arise in all problems.
Andrew,
Can you tell me why conditioning is “tricky and interesting” in settings such
as red state blue state (where causal questions are not involved), what are the
questions asked in such settings that makes conditioning tricky relative to such questions and why is it not ordinary phenomenon expected from conditioning.
Why is conditioning so tricky in red state blue state? I dunno, ask Tucker Carlson.
Judea:
Puzzlement is in the eye of the beholder, many smart people stumble over the arithmetic phenomenon
in the calculus of proportions though puzzlement dramatically increases when a causal interpretation brought up.
But, more interestingly you seem to be suggesting that any description as a purposeful representation of empirical phenomena has to be causally construed – I think it does (its why higher dimensions can matter).
This is the best one I’ve seen:
http://vudlab.com/simpsons/
Andrew B.:
Those are pretty graphs but to me it seems a bit like overkill (perhaps because I’m already familiar with the problem). I like Howard’s B-K plot because it is so clean.
Fair enough. I usually enjoy charts with interactive components.
Wow, I really like this one too! Thanks for sharing.
The portfolios there are excellent. And with animated data visualization, isn’t overkill the point?
Here is a thorough walkthrough which also mentions a Prof. Gelman debate on conditioning (both parties are correct despite contradictory views given the conditioning). http://normaldeviate.wordpress.com/2013/06/20/simpsons-paradox-explained/
Sent from my iShuffle
Is that … Comic Sans?!
Link’s bad:
http://bayes.bgsu.edu/graphics/visual.revelations/vol%2014-15%20(7)/bk.plot.pdf
More generally, isn’t Simpson’s paradox simply misspecification? That is,
Y = xb + u true model
Y = zt + v estimated model
E[t] = (Z’Z)^{-1}Z’Xb
and you can get pretty much whatever you want for t by varying b. This isn’t graphical but is a common presentation in econometrics books from the 60’s and 70’s.
Also, I thought the wikipedia presentation is good and discusses a reference from Pearl to whether to use (in the case of two underlying regimes) whether to use the partitioned or combined estimation is made.
It seems a discussion of the Spanos school of error estimation (he doesn’t like that description, but that’s how it’s perceived) wrt the paradox would be useful. Is there a reference for this?
No, Simpson’s paradox is not simply about misspecification. It occurs when marginal and conditional associations have different directions; this can happen even when everything statistical is correctly specified.
Whether you view the conditional or marginal association (or neither) as the “right” thing to estimate depends on context. But they are not the same, and this is the paradox/puzzle. Thinking about causalilty can be helpful when choosing which to estimate; see Larry W’s section on What’s the Right Answer.
sorry: they are not in general the same
I couldn’t agree more. You get a different answer when you condition on the percentage of women, but that doesn’t mean that such conditioning is appropriate. One can say that treatment A is more effective only by making additional assumptions.
If the treatments are pills, then sure, in the future everyone should get pill A, all else equal. But if the treatments cannot be replicated easily, perhaps because they’re two hospitals, serving different populations, then one might conclude that Hospital B is more effective. Even though the treatment offered by Hospital B is less effective (conditional on gender), Hospital B treats a population that responds better to any treatment, so additional funding should go to Hospital B.
I think this presentation doesn’t do enough to emphasize the paradoxical nature of the finding. It’s in the table, but it doesn’t exactly leap out at you. I don’t see how to present the “paradox” except in natural language. Something like this:
Men respond better to treatment A, Women respond better to treatment A. But overall, people respond better to treatment B.
Ragout,
Agree, English language emphasizes the paradox more that other presentations.
But compare:
1. Men respond better to treatment A, Women respond better to treatment A. But overall, people respond better to treatment B.
2. Seatbelt users respond better to treatment A, Non-seatbelt users respond better to treatment A. But overall, people respond better to treatment B.
Are you as surprised?
Which treatment would you recommend for the population as a whole?
see Fig. 1 (c) in my American Statistician article.
I think I see your point: seatbelt use is something people chose, and that changes our view about which estimator captures a causal effect.
So, if treatment A is an additional safety measure (such as airbags) that is beneficial to both seatbelt users and nonusers and treatment B is an incentive to use seatbelts (such a fine for failing to bucking up) then we might prefer treatment B. Certainly an analysis that conditioned on seatbelt use would be “misspecified” and tell us nothing about the causal effect of seatbelt fines.
What does it mean for the concept of “true causal effect” not to mean much?
dcmaster,
See my post above. To me, saying “”true causal effect” do not mean much” means
disinterest in understanding why context changes opinions about correct actions.
Dvmaster:
Red-blue is an example. There’s no treatment involved at all, I’m just looking at different sorts of comparisons in the data. Comparisons can be interesting and important even without a causal question. I’m not dismissing the importance of causal inference (obviously not; look at the title of this blog!), I’m just saying that puzzles of conditioning arise even in non-causal settings, which suggests to me that causal reasoning is not necessary for the understanding of these problems, even though in many settings it can be useful.
Andrew:
Can you expand on how, without causality as a goal and faced with Simpson’s paradox, you decide which comparison to make? Or if choosing a single comparison seems unrealistic, how you choose which comparisons to prioritize or emphasize, when there are many available?
Fred:
In general I would not decide which comparison to make. My goal would be simply to understand how the different comparisons coexist. This comes up in Red State Blue State. The point is not to find a single comparison or come up with a single “beta” but rather to understand the relations between the variables.
Again, I do agree that, in many cases, causal relations are crucial, in which case we are trying to understand relations among various unobserved variables (which could be called potential outcomes).
To illustrate this puzzle, I’d recommend making up a toy example with all the numbers rounded off to the thousands so that people trying to follow along have a chance to do the arithmetic in their heads using simple fractions.
And pick some omitted variable that isn’t politically controversial. Identity politics variables like gender tend to make moderns get very, very quiet out of worry that they’ll get in trouble for saying (or maybe even thinking) something sexist. College students are repeatedly indoctrinated in the idea that they are supposed to use most of their brainpower to prove that identity politics categories like men and women are actually exactly equal if you think about it hard enough. Giving them an example like the Treatment one where men and women are quite different tends to get them confused.
So, it’s best to pick something that’s not very politicized. These days, age isn’t all that controversial of a variable (which seems surprising to an old coot like me who remembers the Sixties). So building examples around age is pretty safe. You are allowed under the current zeitgeist to think hard about differences between age groups.
I am a bit surprised by the linguistic point of this. Paradox is a traditional name for lots of things that are simply strange as a matter of first impression, but actually can be explained in the correct framework. Cf. Gibbs paradox, twin paradox.
Andrew: “I have mixed feelings about this particular tool as I often work in settings where the concept of “true causal effect” doesn’t mean much”
I see where you are coming from. But just because we can never remove the veil of ignorance we should not abandon precision in our language.
To understand attrition or Simpson’s paradox or many other problems the best way to proceed is to first pretend we are God, and we know the true causal model. For this it is useful to have a causal language. Next we play with the model to understand its implications, identify the source of the problem, and define it. Finally, we want to identify diagnostic tests such that when we stop pretending we are God, we can diagnose the underlying model from this side of the veil. Naive Bayes really.
For all these reasons I would strongly encourage the teaching tool — irrespective of whether one believes in true causal effects or not.
I highly recommend Iverson’s Turing Award Lecture http://amturing.acm.org/award_winners/iverson_9147499.cfm
Thanks for the link.
When I took a seminar from Iverson on the use of J (later form of APL) for teaching calculus he commented at one point – “these are things I wish were pointed out to me when I started to learn calculus – I needed them pointed out. You might have not. Students vary in this – unfortunately its likely all we can do is perhaps needlessly point out to them what we needed to have pointed out to us.”
I think that might apply here too.
Fernando,
Thanks for the link.
Beautiful arguments for the role of notation in thinking and in science.
Exactly the kind of appreciation we need in handling Simpson’s paradox]
(as opposed to Simpson’s reversal, which can be explained with the old notation, hence
became the center attention for those who see nothing causal about the paradox)
I always thought of Simpson’s paradox as just a pure dilemma – the graphs just help to show it. However, it does have the feeling of “okay, the aggregation decision makes a difference, now what?”
It reminds me of something a professor told me – “the results of analysing a data set can make the initial question(s) that you were asking of it meaningless”. I think Simpson’s paradox sits in this area – it makes you wonder “have I asked the right question?” In that treatment table, you could characterise this as “is treatment A or B better?”. But perhaps a more appropriate question is “why did the females have such a higher rate of survival compared to males?” – this difference is bigger than both the aggregated and disaggregated treatment effects.
Also, the treatment example is much easier to “resolve” because all the relevant information is at the “unit level”. A much murkier concept would be to replace “treatment” with “school” and “survival” with “pass the course”.
Pingback: Interesting links for, ahem, “forecasting Fridays” | Pseudotrue News
Pingback: Causal Analysis in Theory and Practice » On Simpson’s Paradox. Again?
Pingback: Causalidade e Paradoxo de Simpson: debate acalorado entre Judea Pearl x Andrew Gelman. | Análise Real