Pro tip: Don’t believe any claims about results not shown in a paper. Even if the paper has been published. Even if it’s been cited hundreds of times. If the results aren’t shown, they haven’t been checked.
I learned this the hard way after receiving this note from Bin Liu, who wrote:
Today I saw a paper [by Ziheng Yang and Carlos Rodríguez] titled “Searching for efficient Markov chain Monte Carlo proposal kernels.” The authors cited your work: “Gelman A, Roberts GO, Gilks WR (1996) Bayesian Statistics 5, eds Bernardo JM, et al. (Oxford Univ Press, Oxford), Vol 5, pp 599-607”, i.e. ref.6 in the paper.
In the last sentence of pp.19310, the authors write that “… virtually no study has examined alternative kernels; this appears to be due to the influence of ref. 6, which claimed that different kernels had nearly identical performance. This conclusion is incorrect.”
Here’s our paper, and here’s the offending quote, which appeared after we discussed results for the normal jumping kernel for the univariate normal target distribution:

And here’s the relevant result from Yang and Rodriguez:
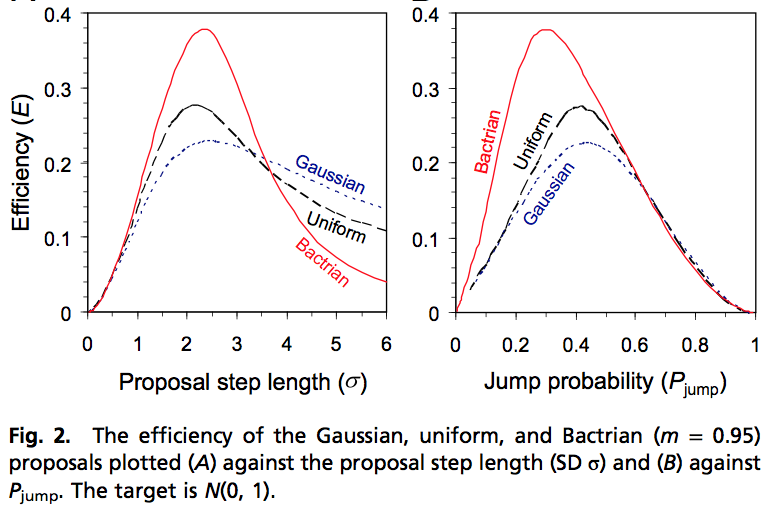
By “bactrian,” they mean a bimodal mixture of two normals.
It looked like in our paper we’d been flat-out wrong, so I spent a few minutes and wrote a little R program, simulating 1-d Metropolis algorithms and computing expected acceptance probabilities, summed autocorrelations, and expected squared jumped distance:
sims <- function (kernel, scale, n_iter, m=.95){
k <- length (scale)
x <- rnorm (k, 0, 1)
x_save <- array (NA, c(n_iter,k))
p_save <- array (NA, c(n_iter,k))
esjd_save <- array (NA, c(n_iter,k))
for (i in 1:n_iter){
if (kernel=="normal")
x_new <- rnorm (k, x, scale)
else if (kernel=="uniform")
x_new <- runif (k, x-0.5*sqrt(12)*scale, x+0.5*sqrt(12)*scale)
else if (kernel=="bimodal"){
shift <- m*scale
width <- sqrt(1-m^2)*scale
x_new <- rnorm (k, x + sign(runif(k,-1,1))*shift, width)
}
else stop ("no kernel selected")
p <- pmin (1, dnorm(x_new,0,1)/dnorm(x,0,1))
x <- ifelse (runif(k) < p, x_new, x)
x_save[i,] <- x
p_save[i,] <- p
esjd_save[i,] <- p*(x_new-x)^2
}
eff <- rep (NA, k)
p_mean <- rep (NA, k)
esjd <- rep (NA, k)
for (j in 1:k){
corrs <- acf (x_save[,j], lag.max=round(sqrt(n_iter)))$acf
eff[j] <- 1/(2*sum(corrs)-1)
p_mean[j] <- mean (p_save[,j])
esjd[j] <- mean (esjd_save[,j])
}
return (cbind(scale,eff,p_mean,esjd))
}
norm <- sims ("normal", seq(0.1,5,0.1), 10000)
unif <- sims ("uniform", seq(0.1,5,0.1), 10000)
bim <- sims ("bimodal", seq(0.1,5,0.1), 10000)
(Sorry about the lack of indentation; that's what seems to happen when we use the *code* tag in html.) [Ed. fixed --- you want to use "pre" not "code", and then you have to escape the less-than signs that are not followed by a "-" because, well, because it's WordPress and their markdown makes as little sense as everyone else's.]
Anyway, the simulations confirmed that Yang and Rodriguez were correct: we had been flat-out wrong in that passage from our influential 1996 paper.
The funny thing is, it was always my intuition that the uniform and, even more so, the bimodal jumping distributions would do better than the normal in that 1-d case. I must have made a mistake in my simulations, back in 1994 or so, leading to that erroneous paragraph in our paper.
Indeed, it is obvious that a normal jumping kernel is a poor choice in one dimension, and I’m embarrassed to have not rechecked our claims, back then!
That said, I doubt that these results will make much difference in higher dimensions where a normal kernel is close to a uniform draw from the sphere, so that you actually are moving some reasonable distance on each jump. And in some applications, a unimodal kernel could have some advantages in that in some sense it could be considered as an adaptive solution, in that it occasionally makes small jumps and occasionally big jumps. Indeed, perhaps a longer-tailed jumping distribution such as a t_4 could be even safer as a generic jumping rule in an algorithm that uses one-dimensional Metropolis jumps.
I haven’t been thinking too much about these things lately because now I’ve been fitting my models in Stan, which uses Hamiltonian Monte Carlo and works in multiple dimensions. I encourage Yang and Rodriguez to try out their model in Stan, I suspect it might work very well for their examples.
I think this mistake would have made it through the review process anyway, though. Suppose you had included a figure that showed (purportedly) the figure that was “not shown” in the paper. It presumably looked very similar to the one that was included — it’s not like you were lying about that. No reviewer would have said “I don’t believe the figure, I want to see the code, and I’ll check it and then run it myself.” Most reviewers would have shrugged and said “well, I guess my intuition about this isn’t very good”, and accepted your results.
It’s a cautionary tale about how we should all be careful — I just caught a coding error of my own that would have led to seriously incorrect inferences — but I don’t think the review process would have helped in your case. Which is indeed sobering.
Phil:
I don’t remember what I did, but it’s likely that I just did some disorganized simulations and never made a figure. I wrote “the results (not shown),” but these results could well have just been some computer output. Had I put something down in the paper, I think I would’ve looked at it more carefully and not made the mistake. Or, had I not put in that paragraph at all, others wouldn’t have been misled.
I think in econ the general movement is towards changing “results (not shown)” to “results (in appendix)”.
The benefit is that it makes this particular kind of mistake less common. The cost is another 10 pages of tables and figures in a paper that is already 20 pages too long. I think its probably worth it. If you want to cite results that aren’t part of the main paper, put them in an online appendix. I think some econ journals are moving towards requiring that your code at least produce all “not shown” results if not format them attractively.
“I don’t remember what I did, but it’s likely that I just did some disorganized simulations and never made a figure.”
Andrew, does this convince you to put in the effort to release code (+data) with papers you publish? Just putting results in an appendix is not much help if one doesn’t know exactly how the results were generated.
Apropos of nothing, I did my first ever Stan-based analysis this past weekend. I modified the errors-in-variables model code here to account for the hierarchical structure of my data set. Point being: Stan is awesome, and the members of the Stan team are awesome for making it happen. (When y’all get around to putting variational inference into Stan, you should check out Black Box Variational Inference by Rajesh Ranganath, Sean Gerrish, and David M. Blei.)
We’re working with Rajesh Ranganath, Dave Blei and Alp Kucukelbir (a post-doc of Dave’s) on putting black-box variational inference into Stan. There are lots of alternatives on the table that we’re currently evaluating.
We’re also working with a phenomenal team on black-box EP (Aki Vehtari, Nicolas Chopin, John Cunningham, Christian Robert, Pasi Jylänki) to put black-box EP into Stan.
We’ll be doing both batch and stochastic versions of EP and VB. Matt Hoffman (who was a student of Blei’s and post-doc of Gelman’s) is the guy who developed both stochastic VB and the NUTS sampler for Stan!
Andrew’s also knee deep in marginal maximum likelihood, so we’ll also be doing that, too, with Hessian-based uncertainty propagation and maybe some light Monte Carlo around the edges. Marcus Brubaker and Ben Goodrich already have the basic penalized MLE with Hessian-based uncertainty working. It’s going to be the summer of point-based estimation and approximation for Stan.
Hopefully, we’ll also get a speedy version of Riemannian HMC, but we’re still down in the trenches of reworking higher-order auto-diff for that (which will also be handy for the black box algorithms that need Hessians). Michael Betancourt has the prototypes all working, it’s just that they’re slow with our current higher-order auto-diff.
Perhaps needless to say, this is all going to take a while.
Wow! That’s fantastic to hear! (Well, not the “take a while” part, but as the old saw goes: Quality, price, speed — pick any two.)
Just to say thank you for pointing out such things in your blog! I’d like to live in a world in which all scientists are as open about their mistakes. Unfortunately I don’t.
I must have made a mistake in my simulations, back in 1994 or so, leading to that erroneous paragraph in our paper.
Will a retraction follow? There is no stature of limitations on bad papers, right?
DK:
1. It’s not a bad paper. It has a mistake, that doesn’t make it a bad paper.
2. I would publish a correction but the paper appeared in a proceedings volume, not a journal.
Does “proceedings volume” mean it was peer reviewed or not? Just curious.
I think it was peer reviewed but I don’t recall. In any case it doesn’t really matter now!
True, it doesn’t matter for this case. In general though, I’ve a complaint against these quasi-journal modes of publication. Conference Proceedings etc.
Often times they look indistinguishable from a proper peer reviewed publication especially when found by searching online. They give a false sense of legitimacy / credibility to non-peer reviewed work passing off as peer reviewed work (not targeting Andrew’s paper). Then again there’s the no-corrections-possible drawback etc.
I’d rather that people just go to conferences and just present work. Maybe publish abstracts at best. Or release videos or slides. But this parallel channel masquerading as true journal articles annoys me.
/rant
I disagree. If you go to a conference and present a paper, a few tens or hundred people will hear it and probably forget about it. If you publish a proceedings at least people will be able to see what you were talking about and what your thoughts were. Proceedings papers are pretty clearly what they are… not reviewed, but useful as a documentation of what people are working on, who had what kinds of ideas, etc.
Maybe they ought to watermark each such page with a big “Not Peer Reviewed” stamp.
So what’s your opinion on other papers citing such stuff? We could develop a house of cards. Maybe peer review would have caught Andrew’s fault? Maybe Yang and Rodríguez shouldn’t be giving that much credence to non peer reviewed work? I suspect they didn’t even realize it was not peer reviewed.
Also exactly where in this citation do I get to figure that it’s non reviewed tentative work? “Bayesian Statistics 5, eds Bernardo JM, et al. (Oxford Univ Press, Oxford), Vol 5, pp 599-607”
Rahul:
As I said in my earlier comment, I think our paper was peer reviewed. So I really think you’re going off the deep end here.
@Andrew:
No. I’m just using your paper as an example. If it was indeed peer reviewed, great. I’m just against non peer reviewed proceedings. Your specific case shows how difficult (impossible?) it is to know whether or not a proceeding was peer reviewed.
This stuff really poisons the well.
“Maybe peer review would have caught Andrew’s fault? Maybe Yang and Rodríguez shouldn’t be giving that much credence to non peer reviewed work?”
Rahul, do you know of any evidence that “peer review” performs the functions you are ascribing to it? Even better, what conditions need to be met for it to do so and how often are these conditions met in reality (eg peers actually reading the paper carefully)? I have looked for it, as well as asked around, but only found assumption and negative commentary about peer review. I asked this previously in a different thread on this site, if I was responding to you sorry for repeating it.
@question
No, I know of no evidence. Maybe there is. I don’t know.
But I work on the belief that peer review helps, I think the whole system does. If it’s useless, or worse dangerous, then let’s get rid of the whole charade. But that’s a different story. I just don’t want the confusion of people thinking something is peer reviewed when it is not.
question: As author, reviewer and associate editor I saw lots and lots of papers improved (including my own) and unjustified statements removed by the peer review process.
Daniel:
Here is a neat example.
I agreed to review a paper, one of the authors of whom had attended one of my talks in the past and I expected was very capable of making an important contribution (that why I agreed).
They had essentially written up the presentation I gave at that talk, but had failed to address a serious criticism that had been raised by someone at the very same talk (that lead me to abandon that line of research).
After it was discussed with the Associate Editor, Editor and some others who were at the same talk, it was decided that they very likely just totally forgot what I had presented, and so I did the review.
Pretty sure this has happened to others.
It just seems strange to me that peer review is held up as a “pillar” of reliable science, yet no one bothers to justify the behaviour with empirical evidence or study when it is effective.
Rahul, I agree that it is wrong to present non-peer reviewed work as peer-reviewed since, right or wrong, so many people seem to put stock in it.
Christian, your anecdote sounds plausible and I am sure that scenario occurs often enough, but that is not the end of the story. How common is a positive experience vs a negative experience, and under what conditions does each occur so that we can foster the positive? Is the current method of tying peer review to the journals really optimal? Would just publishing a pre-print and asking for comments from anyone interested be more effective? Why aren’t the reviews included with the publication? In fact I propose that every publication should be accompanied by a critique, if only to point out the technical difficulties and sources of controversy. Let the reader decide if the critic is right or wrong.
What are the drawbacks and what is the net value? Some possible drawbacks could be slower time to publication, inappropriately enforcing social norms / group think (thus hindering innovation and/or perpetuating undesirable behaviour such as misinterpreting p-values), and undue control over what is deemed “reliable” or “interesting” information by established people with vested interest.
Even if this evidence does exist somewhere I am convinced that most researchers are unaware of it and are acting out of faith.
Rahul,
What are you supposed to do if you have no peers? I’m peerless for example.
You could “publish” a correction on your home page next to the link to the article.
Done.
I think Andrew is being highly critical of himself and very generous to others. I admire him for that.
Regarding some comments above, I think that Andrew’s paper is by no means a bad paper. It is one of the most influential papers on MCMC efficiency and is well cited. Our paper, which criticized one conclusion from that paper, followed exactly the same procedures.
The two paragraphs quoted above from Andrew’s paper, which we criticized, include results for two specific kernels alternative to the Gaussian. The first is the uniform kernel. This we found to be more efficient than the Gaussian kernel (efficiency = 0.276 versus 0.228) applied to the N(0, 1) target, when both are at the optimal step lengths. The difference is real but not that great, especially given that the two methods for calculating efficiency are affected by numerical errors (the matrix method by the number of bins used in the discretisation and the MCMC simulation method affected by the length of the chain and the difficulty of calculating ACF etc.). The amount of computation to optimize the kernels is in the order of minutes (near 1 hour, I think), but must be much longer on computers of 20 years ago. Thus I think the difference in efficiency could easily go unnoticed.
The second alternative kernel Andrew considered is a Gaussian mixture. I think I tested this but because its two humps are too close to each other it is not (much) more efficient than the uniform or the Gaussian. So here there was no mistake. We found better mixture kernels (with the two humps far apart and spiky) only when we looked at the whole class more systematically.
Thus my rough guess is that Andrew’s conclusion that the different kernels had nearly identical performance might perhaps be due to a slightly too hasty summary of limited simulation results. I don’t think such a mistake is likely to be spotted by a reviewer. I don’t think it matters whether or not the paper went through a proper review.
Ziheng
Pingback: Weekend reads: A call for retraction of therapy-breast cancer study; credit (and pay) for peer reviewers | Retraction Watch