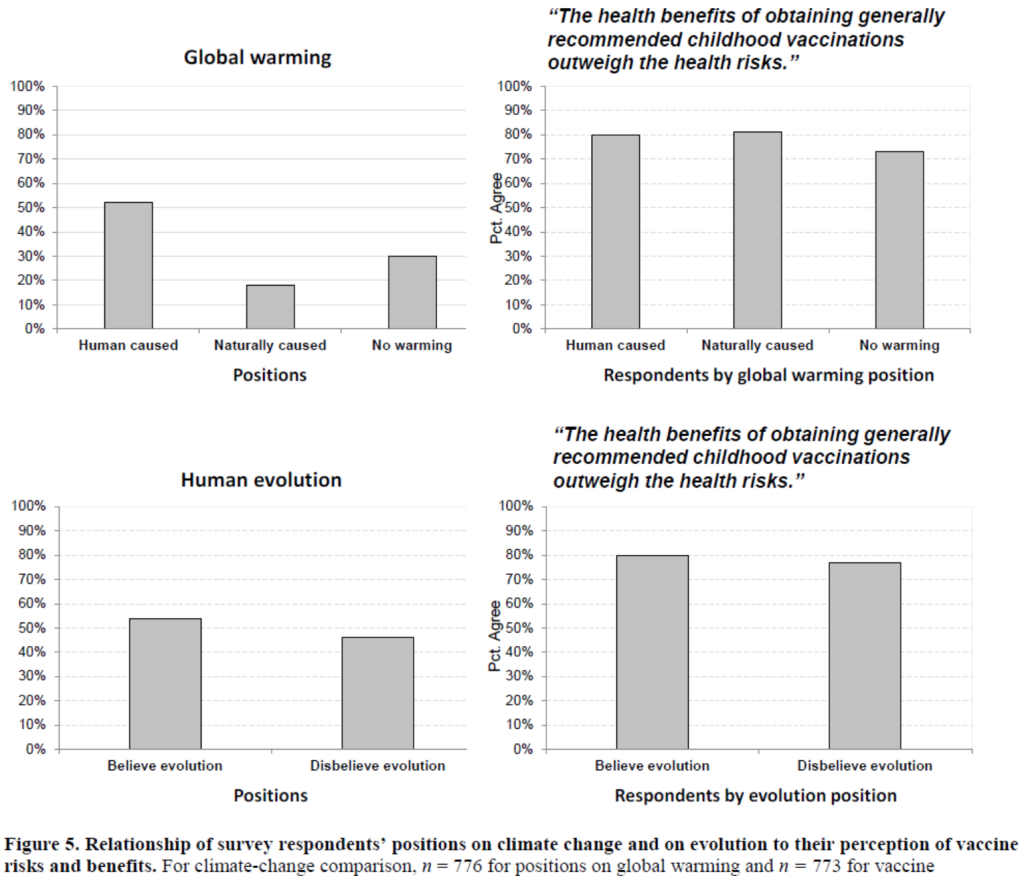
“False parallelism”—feel free to come up with a better term here—is when a graph has repeating elements that do not correspond to repeating structure in the underlying topic being graphed.
An example appears in the above graphs from Dan Kahan. The content of the graphs is fine (and, more generally, I think he’s making an important point that we all should be understanding more). But I have a problem with the display, which is that the graphs on the left and the right are displaying different sorts of things but are being shown in parallel ways. The graphs on the left show percentages that are constrained to add to 100%; they’re numbers that could (for example) be displayed in pie charts. Mathematically, each of the left graphs is a histogram of a (simple) probability distribution, which one might call p(x). But the graphs on the right show proportions of a different variable, as a function of x. They are graphs of E(y|x). I always find such juxtapositions confusing. The graphs look the same—they even have the same scales on their axes—but they’re showing different things. Some cues are provided by the axis labels, and indeed I ultimately did figure out what they were saying—but it took time, and the effort required to decode the graphs took me away from the big picture.
How would I do it? I’m not sure. I’d probably start with something simple: Just ditch the graphs on the left entirely, and then on the graphs on the right, make the width of the bars proportional to the percentage of people who gave each response. Also I think I’d extend the bars up to 100% so they are gray on the bottom and white on the top; this would emphasize that each of these is a proportion out of 100%.
I’m not saying this suggestion of mine is perfect. My real point is that the structure of a graph sends Gricean messages. We should be aware of these messages and use them to our advantage, not let them use us.
Hey, that was fun! I haven’t done a pure graphics post in awhile.
The y-axis on the righthand graphs could be the count; each bar fill could reflect the specific count asnwering affirmative/negative. If the contrast in proportions across the bars wasn’t clear, you could just label them with the % value. 2 more cents.
This looks like a good application for mosaic plots (Micheal Friendly is the name I always associate with these). There are a number of R packages that support them. They are really good when the goal is to visualize the conditional (in)dependence of two variables, which seems to be the goal of the plots you quote.
Correpndence plots might be worth considering – http://en.wikipedia.org/wiki/Correspondence_analysis
Unfortunately at one time there was an error in the SAS documentation that lead almost everyone (including Micheal Friendly) to incorrectly adjust the plot.
This explains things very well – Greenacre, Michael (2007). Correspondence Analysis in Practice, Second Edition. London: Chapman & Hall/CRC.
Including in what sense they are sensible residual plots of assumed models of independence or adjusted independence.
Well, every vaccine I’ve looked into had problems with the evidence. They never seem to be able to distinguish between affecting disease incidence vs disease diagnosis rates. Just look up the changing diagnostic criteria for polio. Things are not so clear cut as people think.
Hadley Wickham had some interesting ideas in http://vita.had.co.nz/papers/prodplots.pdf
It’s about marginal, conditional and joint discrete distributions and how to plot them. From Hadley’s perspective, your idea of adjusting the width of the bar amounts to displaying the joint distribution, not the conditional.
One way to displaying it may be to use not two but three plots, as in his figure 5 (there is a typo in this figure, the first ‘=’ is a ‘x’).
You’d have a x b = c with:
(a) the marginal distribution p(global warming)
(b) the conditional p(vaccination | global warming)
(c) the joint p(global warming, vaccination)
The co-author of this work, Heike Hofmann, has been made invisible here. Hadley Wickham … Hadley’s perspective … “his” Figure 5.
Andrew is describing a spineplot and I think that is the best solution for these pairs of variables too. It would be interesting to have the data for all three variables together. Some variant of a mosaicplot could then be effective.
There is a minor feature in the second set of data, which is shown by drawing side by side barcharts. The numbers of those who disagree are about equal for the two groups, but there are more in the first group who agree. Rather than seeking a single optimal display, it’s useful to look at the data in several different ways.
Not to cause trouble, but it looks to Eli like a table would be a lot simpler to figure out and more informative. If the amount of data is small a table is almost always better unless you want to show a trend with independent and dependent variables.
Eli:
I disagree completely. I mean, sure, a good table can be better than a bad graph, but I’d prefer a good graph to a good table, even in this setting where only 8 numbers are being displayed. For one thing, if you do the graph well (in the above example, we can do it with 2 graphs rather than 4), you can take up very little space and then use small multiples and display a lot more.
That said, making a good graph takes more work, compared to making a good table. So there is that tradeoff.
Andrew,
With all respect, if this were true we would all write in Chinese characters
Oh, come on, Chinese characters are not visualisations of sememes, phonemes or even alphabetic graphemes – they bear no relation to them, at all. Regardless of eventual ideographic correspondences in their origin, any sign-sememe or sign-phoneme correspondences are completely arbitrary today. This is not, at all, how a graph corresponds to a table. With all respect, this is a faulty comparison.
I’m with Eli on this one. this seems like a case where a Table would totally suffice. 4 charts for 8 numbers seem gross overkill.