Andrew Dolman writes:
Just in case you need another example of why it is important to consider what the intercepts in a model represent, here is a short comment I [Dolman] just got published correcting a misinterpretation of a simple linear model, that would not have happened if they had centered their predictor around a sensible value.
The actual topic here is “Macrophyte effects on algal turbidity in subtropical versus temperate lakes.” That is so cool! I google-imaged “algal turbidity” and found the above pretty picture, which is on a webpage with a full discussion of turbidity. Surprisingly interesting stuff.
Back to Dolman and interpreting the intercept: Here’s his graph:
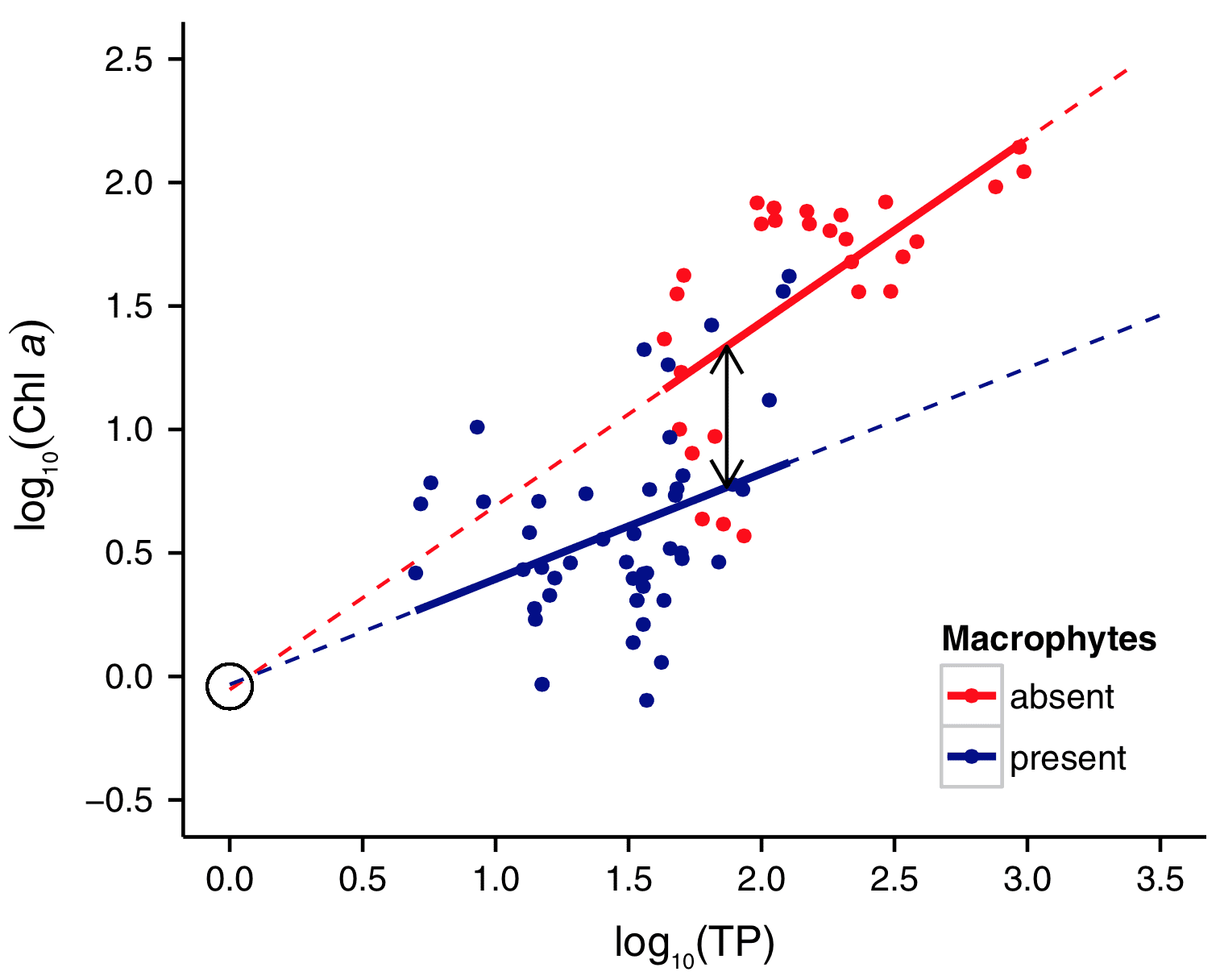
You can perhaps already see what happened. The other researchers noticed that the two lines had essentially the same intercept, and they concluded that the two groups differed only in the slopes, not the level of the lines. But this was a mistake in the context of the data. It’s similar to the example that Jennifer and I give in our book with the regressions of earnings on height. The intercept of such a regression doesn’t have much meaning, as it corresponds to the earnings of someone with a height of zero inches.
FWIW I think the original interpretation is right … these lines vary in their slope. At that point talking about differences in intercept completely arbitrary since one could reasonably justify “centering the data” so that the minimum observed value for TP is adjusted to equal zero or the mean value of TP is adjusted to zero, or the media, or whatever.
In other words the intercept is always some arbitrary point along the observed relationship regardless of how the scaling is adjusted and who’s to say there aren’t some reasonable theoretical reasons for wanting to know what the difference in Chl is at zero TP.
Anon:
The lines definitely differ in their slopes. The problem is in the interpretation of the intercepts. It’s possible that people care about the intercept in the above graph, but I doubt it. It’s on a scale of log(TP), not TP, so the intercept is the predicted value when TP=1. But, sure, if that happens to be a natural point on the scale, I agree with you on the interpretation. The real point is to have a natural value for the zero in the model. If zero on the original scale makes sense, you can use the raw parameterization. If not, I think it makes sense to center at some understandable value. In many cases the mean is close to something understandable, so centering at the mean can make sense. So I think it’s a good default choice to center at the mean. But, in any particular application if you have another reasonable centering value, go for it. I often use the center of the scale, for example if party ID is on a 1-7 scale, I shift it to a -3 to 3 scale, so that Independent = 0. But I wouldn’t want to simply use 1 to 7, which is the sort of thing that people often do without thinking about it.
Author (Dolman) here.
@Anon
The slopes were not “statistically significantly different” either so in fact they concluded that, as neither the intercepts nor slopes were different, there was no difference between the two lines. But the difference in intercepts is for lakes with a total phosphorus concentration (TP) of 1 µg L-1, which is extremely low and far outside the range of these data.
I centred on TP = 74 µg L-1, which is midway between the first lake with no macrophytes, and the last lake with macrophytes. So the intercept is not exactly arbitrary – it can be interpreted as the midpoint of the range of TP concentrations during which lakes transition between the two states (macrophyte and non-macrophyte).
@ Dale Lehman
Yes, centering is context specific. The point is – if you want to interpret the estimated intercept (or differences) then you must check what they really represent. In this case I would not expect a difference in intercepts for lakes with TP = 1 µg L-1, at that kind of phosphorus content there will be very little phytoplankton regardless of other factors.
I’d like to add that there was a lot more to the original paper (Wang et al 2014) and the authors were very helpful when I approached them about this error. In fact this was an example of science working perfectly. I spotted an error, the authors supplied the data, I checked my suspicions and wrote it up, submitted to the original journal, a reviewer pointed out that my discussion was a little over simplified and out of date, I fixed that and it was accepted.
Naive question: Is macrophyte coverage sufficiently clear cut to represent it by a Yes / No variable rather than a smooth, varying parameter?
Good question. I don’t know the answer; I couldn’t find anything about it in Dolman’s paper.
Additionally, I wonder if the messiness is, in part, because we are asking the wrong question.
i.e. Rather than ask (a) “Are they different?” wouldn’t (b) “How different are they?” be a better question?
I’m not sure what the “they” refers to in your question. Please clarify.
@Martha:
Sorry. My bad.
By “they” I meant the log10(Chl a) versus log10(TP) relationship in vegetated and non-vegetated lakes.
i.e. (a) Is the log10(Chl a) versus log10(TP) relationship different in vegetated lakes versus non-vegetated lakes?
Talking about differences in intercept is arbitrary, but I think that was the point, which is why the original interpretation seems mistaken. So instead of arbitrary choice of X, compare differences at some non-arbitrary value of X like the middle of the overlap or either of the edges of the ranges. I also note that the original authors replied to Dolman’s comment and didn’t seem to get Dolman’s critique as they seem to think that Dolman didn’t re-center the data at another X but instead simply limited the analysis to those points around the new X.
I have never completely understood the centering issue. In fact, I just covered this example in class last week. Here is regression output for real estate data where there is an interaction between the number of bedrooms and number of bathrooms. With the interaction effect centered, the parameter estimates look like:
Intercept 95133.618477
Beds -7553.856503
Baths -7453.282501
(Baths-2.34584)*(Beds-3.48316) -9526.410636
SF-Res 127.12790563
School-High[Bartlett] -22409.73361
School-High[BTV-Undiscl by LL] -10804.24505
School-High[Chugiak] 42719.626194
School-High[Dimond] 16298.275032
School-High[Eagle River] -75897.99519
School-High[East Anchorage] -16532.06286
School-High[Service] 15526.547405
School-High[South Anchorage] 50955.53569
As you can see, the coefficients for beds, baths, and the interaction are all negative. If we don’t center the polynomials, the parameter estimates are
Intercept 17294.066721
Beds 14793.539422
Baths 25728.728337
Baths*Beds -9526.410636
SF-Res 127.12790563
School-High[Bartlett] -22409.73361
School-High[BTV-Undiscl by LL] -10804.24505
School-High[Chugiak] 42719.626194
School-High[Dimond] 16298.275032
School-High[Eagle River] -75897.99519
School-High[East Anchorage] -16532.06286
School-High[Service] 15526.547405
School-High[South Anchorage] 50955.53569
I find the uncentered estimates much easier to interpret. In either case, both the intercept and slope are changed by the interaction, but I think the second model is much easier to understand. Of course, the models are equivalent, but I have never found it particularly easy to interpret models with centered coefficients.
In a case like this, the question is whether a linear predictor makes sense through the entire range from 0 up to 3 or 4 or whatever. I notice that it’s a Log_10 scale. So in this case it isn’t a “person with zero height” or whatever, it’s a situation where TP = 1 whatever TP is.
Over small ranges of a predictor variable, the justification for linear fit is basically that you’re estimating a first order taylor series for the “real” function. Obviously, outside of some portion of the domain, that may not make sense. By centering the data, your interpretation is more directly in terms of the taylor series: Y = a + b*(X-X_0) is the first order taylor series *around* X_0.
Although you can always rewrite that model as Y = a-b*X_0 + b*X, it becomes much more confusing, and appears at first sight that you believe the linear model for the entire range from X=0 all the way through the region around X=X_0
So, while the weight of a person of height = 0 should be 0, the function weight vs height is NOT a linear function all the way from X=0 through X=typical weight of an adult.
In the turbidity case, because the variables are log transformed, it seems that the intercept is pretty much meaningless anyway. This would become clear when you realize that you can’t take the logarithm of a quantity that has dimensions (units). So you should really define dimensionless ratios
TP/TP_0 and Chla/Chla_0 and then log transform those. The TP_0 and Chla_0 are both arbitrary, *and* determine the zero location of the scales. In other words, because log(a/b) = log(a)-log(b) they entirely determine the intercept term.
Dale:
I think your results are so difficult to read in part because you have way too many digits. I’d recommend the log scale. Or, if not that, divide all your numbers by a 100,000 and present results to 1 decimal place. Regarding the centering, instead of centering at the mean of the data, try centering at a round number with a clear interpretation, for example 2 bathrooms and 3 bedrooms. I have a feeling that the result will be much easier to read and understand.
Yes, of course the digits should be reduced – the display was not meant to be a final product. The issue of interpretation has to do with the signs of the coefficients – negative signs on each of beds and baths and on the interaction (centered) is a mess of negative coefficients x some negative and some negative values. Of course they can be interpreted correctly. On the other hand, the non-centered coefficients are sort of straightforward – bedrooms and bathrooms both have a positive impact and a negative impact through their interaction. It is relatively simple to look at how an additional one of each adds to the house value up to a point and diminishes after that. I just think that is harder to see from the centered output.
I suppose my general point is that centering may be context specific. It may depend on the data as well as on the viewer. I’m not sure I buy the idea that centering is, in general, preferred.
I think interpreting coefficients is hazardous, and I teach students to resist it. Centering helps with fitting, so usually worth doing. But few non-statisticians can keep in mind all the weird machinery between parameters and predictions.
Just plotting implied predictions is much easier. It’s still hard for people. But it works much more generally than trying to use marginal distributions of parameters to understand implied predictions that depend upon joint uncertainty in parameters.
In the example in OP, if they had just plotted the data and posterior predictions, they wouldn’t have been so easily fooled. Maybe.
I looked at the paper. I don’t think the problem, if there was one (I can’t tell b/c I don’t know enough about the subject matter) was failing to center the data; it was analyzing the data w/ an invalid model. Whether or not the data were centered, the coefficients for the predictors in the model fit by the original authors show no “significant” difference in slopes; likewise, the coefficients for the predictors in the model fit by Dolman does show a “significant” difference in the slopes– whether the data are centered or not.
Centering the regression outputs easier to interpret– but it won’t tell you whether you fit a valid model to the data. I agree, too, w/ Richard McElreath that graphically reporting the results is a better way to make the regression output intelligible than centering the predictors.
Maybe I’m not getting what happened here, but I would have thought the lesson was that one should look closely enough at the *raw* data — likely by one or another form of exploratory, nonparametric smoothing — to figure out whether the model that one is fitting is valid.
Obviously, subject matter knowledge is required too. I don’t think one can figure out who is “right” here w/o knowing something about where along the range of whatever is being plotted on the x-axis it makes sense to model whatever is being plotted on y-. That’s actually the linchpin of the argument in the second author’s paper: the original authors constructed a model for observations in a zone of x-axis values from which meaningful real-world inferences can’t be drawn. If that’s right, the error was not a “statistical mistake” on the part of the original authors; it was a mistake in the *external validity* of their model– something that one can detect only if one has independent knowledge about the phenomena being modeled.
So in sum, I think the episode is very instructive but the lessons it teaches probably don’t seem to be captured by “center your predictors.”
I agree with dmk38 that “I think the episode is very instructive but the lessons it teaches probably don’t seem to be captured by “center your predictors.”
Here is my take, which might be called a bigger picture.
Lesson 1: Don’t confuse “parameters of the problem” with “parameters of the model”. In this case, the model (two lines one for each of the two categories) had four parameters: Two slopes and two intercepts. But the intercepts (at least with the usual interpretation of “intercept’) could not reasonably be considered parameters for the problem, since their standard interpretation is outside of the range of the data. (To extend Box: All models are wrong; some are useful. But we have to figure out from context what is and is not useful about the model.)
Lesson 2: Data and context are both important. Staring at the graph, it sure looked like there was something going on in the region where the two colors of data overlapped in horizontal coordinate. So I followed the link to Dalmon’s paper, and after a while of looking at it this way and that, I did a figurative head slap when I focused on the phrase “whether total phosphorus (TP) thresholds for regime shifts differ between subtropical and temperate shallow lakes, as well as between lakes of different depths,” in the first sentence of the body of the paper. Yeah, that’s what hit my eye in the graph – the transition between blue and red. That’s what was being studied, and that’s where Dolman did his analysis. Makes sense.
Lesson 3: Words can influence our thinking.
Example A: I was uneasy with the word “threshold” in the paper. What I saw in the graph was what I would call a transition, not a threshold. (That is, I think of a “threshold” as a sharp cut-off point. That’s not what I saw in the graph, but rather a region of transition where blue and red overlapped.) Thinking “transition” rather than “threshold” brought several thing to mind. Maybe attention should be restricted to the transition region, which might even mean that maybe log scale was not best. But then I thought about Andrew G’s admonition never to throw away data. OK, so maybe a weighted regression, giving more weight to the transition region. (But, of course, why not look at something like a lowess smooth when first looking at the data anyhow? )
Example B: The title of Dolman’s paper starts “Macrophyte effects on algal turbidity …” Hmm. “Effects on” suggests causality to me. I don’t know the biology and chemistry well enough to know if there is good scientific evidence that macrophyte presence/absence has a causal influence on algal turbidity (which is measured as chlorophyll a concentration in these studies)
Maybe it goes the other way around? Or maybe both ways? Or maybe there’s some complex interaction between these two variables and total phosphorus? Well, at this point, probably some combination of Andrew Gelman, Judea Pearl, and a limnic biochemist would be better than me at studying the problem (taking prior studies into account, of course.)
from Dolman’s paper:
“It is tempting to draw the conclusion that colonisation by macrophytes causes these lakes to have 53–84% lower chlorophyll a. However, causality here likely runs both ways: for example, colonisation by macrophytes may provide refuges for zooplankton thereby reducing chlorophyll a via top-down effects, but equally lakes with lower chlorophyll a for a given TP concentration (for whatever other reason: depth, flushing rate, temperature, etc.) will also be more favourable for macrophyte colonisation.”
Thanks for drawing attention to this. I was not intending to criticize Dolman specifically. Unfortunately, my experience is that titles, abstracts, and first paragraphs often are what people remember rather than something toward the end of a paper.
Do you think this problem could have been avoided with mixed models? I am still trying to wrap my head around the concept of where it is applicable or not, but it seems that the varying intercepts and potentially (or not) varying slopes seems well suited to its use?
One concern that I haven’t seen brought up here yet is that the fitted slope and intercept are very closely connected when fitting a straight line to un-centred data. Consider: Any time you fit a straight line to some data (using least-squares-based methods, at least), the line must pass through the point (xbar, ybar) (where of course xbar is the mean of the x-values, etc). If you have a straight line pinned at this point, and xbar is not zero, then small changes to the slope result in large changes to the intercept. This means that uncertainty in the intercept has _two_ components: uncertainty in the vertical level of the line, and uncertainty in the slope amplified through the “lever arm” back to x=0.
It goes the other way, as well: if the true intercept is higher, the slope must be lower in order to go through the data. So the uncertainty in the intercept contributes to the uncertainty in the slope.
The most direct way to break this connection is to centre the data at xbar. Any other choice of centring will cause this problem to at least some degree, although obviously if it’s not too far off xbar the effect will be small.
On the other hand, it’s not difficult to calculate exactly how much of the intercept’s uncertainty is due to the slope’s uncertainty. From that you can find out the uncertainty in the “line level”, or for that matter the uncertainty that you _would_ have gotten if you’d centred the data. This is the same as calculating “confidence curves” on regression lines.
So the centring problem comes down to this: The fitted parameters are correlated, but we ignore this when we take the reported uncertainties (which are used to find e.g. p-values) at face value.
What this means is that the most accurate (and smallest!) uncertainties in the slope and intercept of a line are found when we centre the data at the mean. Now, if you want to compare the best-fit lines through two sets of data covering different x ranges (like in this case), you need to propagate the slope and intercept uncertainties properly so that you’re comparing them at the same place — which is equivalent to centring both sets of data to the same value (or leaving them uncentred). My point here is that this parameter correlation is the whole reason why the significance of the comparison is sensitive to where you centre the data.
It also suggests a procedure: If you centre both sets of data to a point half way between xbar_1 and xbar_2, you’ll get the most sensitivity to actual differences between the two fitted lines. Any other choice will give you larger uncertainties in both intercepts and slopes.
(Caveat: It occurs to me that choosing a point half way between xbar_1 and xbar_2 may be naive. For example, if the (true) uncertainty in slope 1 is larger than the (true) uncertainty in slope 2, the most sensitive choice of centre would probably be closer to xbar_1… But if it’s a big enough difference to care about I don’t think it would be difficult to do properly.)
If really looks like the “present” condition should have a negative slope on the regression line. Obviously the two points in the upper left of the cases for this condition are enough to flip the slope around. I would call them outliers and refit the regression but I recall from somewhere on this blog that this is a non-operative concept in modern statistics.
I, of course, meant upper right (spalexsia (spatial dyslexia), I suppose).
I’d be particularly wary of omitting these two points, since they are in the transition zone, which is the subject of interest here. (Unless, of course, there is evidence that there were measurement or recording problems involved in these two data points.)
(PS Maybe dysspatia might be better than spalexia to describe the phenomenon? I often experience it.)
Suppose removing those two points did reverse the slope? How would this be interpreted? I guess the overall point is that there is reason to be quite suspicious of any statistical analysis which depends on a small number of observations (this is why we use the median rather than the mean–the breakdown level is 1/2 rather than 0). You may be correct that the “transition” zone may have special meaning in a substantive problem. Still, I wonder what the Thiel-Sen estimator would show on this condition.
Since there is reason to question whether or not a linear fit is appropriate, the question of interpretation if removing the two points reverses the slope seems moot.
If the models are not linear all the above discussion on the intercepts is flawed. Also, if there is a negative slope, the intercept would be well away from the current one.
@numeric:
In general, why isn’t the Thiel-Sen estimator more widely used for all sorts of linear regression applications? Do you know?
Are there drawbacks? Because it sounds like it would be an ideal fit for a huge chunk of problems.
Well, it’s been called “the most popular nonparametric technique for estimating a linear trend” (El-Shaarawi, Abdel H.; Piegorsch, Walter W. (2001), Encyclopedia of Environmetrics, Volume 1, John Wiley and Sons, p. 19, ISBN 978-0-471-89997-6–I cribbed this from the wikipedia entry so don’t blame me if it is a fallacious reference). Here’s what I think. It is used a lot in scientific fields where contagion is expected (environmental sciences, for example). It takes a little more computational time than OLS but given how fast everything is these days that’s not a consideration. What is really needed is a straight-forward routine (say in R) that calculates the linear regression coefficients, the Thiel-Sen, and then gives a significance test (I know we aren’t supposed to use them, but still, they are convenient) as to whether they are the same. Most will be, but the investigator could then be tipped off to potential problems with those that aren’t. Something in R would be ideal
summary (lm (a ~ b, thiel-sen-check))
and it would let you know in the summary (or a variable) whether it gave the same answer.
For being so “popular” I almost never come across it in papers in the areas I usually follow. e.g. Chemistry, Chemical Engineering etc.
Well, if outliers are the contagion, the contagion is ubiquitous.
My goal for this week is to ask 10 Chemists what Thiel-Sen is. Let me see how many even have heard of it.
Out of curiosity, is there some theoretical reason why this relationship (log(Chl a) vs log(TP)) is being described linearly? To my eye, the story this graph tells is that the relationship between log(Chl a) and log(TP) is a soft step function (like a pH curve). (Also it looks more to me that lakes with and without macrophytes both fall on the same log(Chl a) vs log(TP) curve, but macrophytes tend to be associated with higher TP…)
(My apologies if this is explained in the article — I haven’t read the original Wang et al paper.)
I agree with Erf that fitting straight lines seems inappropriate — particularly since the interest is in a “threshold” (or, as I see as preferable, a “transition region”). It might also be worthwhile (from an exploratory perspective) to look at the graph of the raw data, without taking logs.
Ok, I’m a little late to the party, but I take it that the points on these graphs can be considered as equilibrium points of some kind of feedback differential equation, where macrophytes and algae compete for resources such as phosphorous etc.
If so, I’d like to see that model analyzed directly rather than fitting a couple of lines through some data, and that would be probably very doable using Bayesian methods.
Martha’s comment made me recall a (simulated) example in ARM of sensitivity of inferences to model misspecification due to lack of complete overlap. (A glance at the TOC of the Google Books version suggests it’s around page 199; no preview available.) IIRC, the plot shows two panels with the same data fit to two models. In the first panel, the data are divided into two clusters with a linear model fit within each cluster; the two regression lines have the same slope, but there’s an offset between the intercepts. In the second panel, a non-linear model is fit to the full data (i.e., without regard to the cluster dummy variable); a gentle non-linear transition in the (small) region of cluster overlap provides a good fit.
The data in the plot above could easily be telling such a story, in which case the pair of linear models would tend to give undue weight to data far from the region of overlap…
What I’d like to see would be a panel showing all of the analogous graphs of all the lakes that had been studied, each with a smooth for each condition (and maybe the panel might arranged by some relevant variable) That might be a good data display to explore to get a feel for the general problem, not just for a single lake.
What is the “correct” way to mean center higher order terms? For example, I’ve already included my predictor, x, in the model and it has been mean centered. If I’d also like to include a quadratic term in my regression, would I
1. mean center my predictor, x, and then square it
2. square x and then remove the mean
or
3. square x and not mean center?
I’d appreciate any help. Thanks so much!