I was googling *back of the envelope* for a recent post and I came across these lecture notes by Victor Weisskopf from 1969.
I can no longer really follow this sort of thing—I really really wish this had been my textbook back when I was studying physics. If they’d taught us this stuff, I might’ve never left that field.
Anyway, here’s one of the more accessible bits, from page 8-11 of the document, where he derives that a mountain must be less than 30 km high to be supported by the rock at its base:




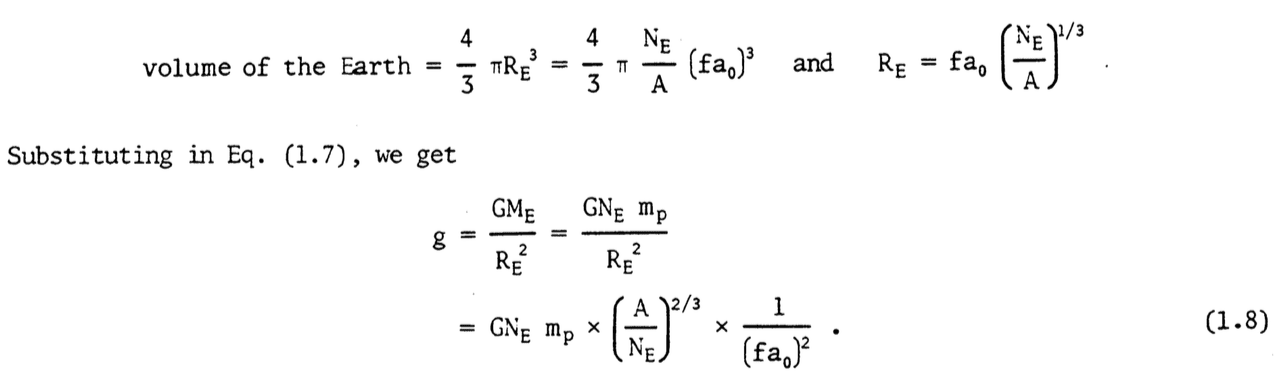

In the next section, Weisskopf derives the number of atoms in a liquid from its surface tension and latent heat of evaporation:


I’m really annoyed that physics wasn’t taught this way to me. That said, it’s a challenge to write a statistics book of this sort. I’m working on it; I have various examples that have this flavor.
I love this kind of stuff. I think they should be teaching this kind of thinking as early as about 4th grade science classes. By the time you are in a proper HS Physics class this dimensional analysis and order of magnitude type calculations should be second nature. At least, it should be second nature for the science-minded kids who were paying attention. But typically this kind of thing isn’t well taught, and even lots of college professors don’t have a grasp on this stuff.
+1
How does Cosma Shalizi’s data analysis book do in this regard? The title is at least similar.
http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/
T:
I followed the link. Shalizi’s book reminds me a lot of the Hastie and Tibshirani books. It’s fine, but, other than the title, I see no similarity to the Weisskopf material excerpted above. I’d describe Shalizi’s as more like the statistics equivalent of a well-written physics book.
Andrew:
I’d love to read a book with this flavor on Stat. Maybe the one you are working on. Can you post any of the Chapter drafts online?
Or blog about any of these Stats examples you mentioned that have this flavor? Thanks!
I like the idea of this kind of analysis, but when I see examples like this, I am nagged by the feeling that I am being sold snake oil. The results depend on modeling assumptions and approximations, which is fine, but they need to be validated. In this case the model predicts the height of mountains on earth, but I wonder how much tweaking was needed to make it work. Or how many other models didn’t work and didn’t get published. If this model correctly predicts the height of mountains on other planets, or mountains made from other materials, I would be more excited about the methodology it demonstrates.
Checking should be a simple ratio. They get h<= E_liq/(A*m_p*g). Mars has surface gravity of .376g, so the tallest mountain on mars should be about 1/.376~2.66 the tallest on earth, assuming they are made of the same materials, etc. Olympus Mons is 21-26 km high (depending where you measure from), Mount Everest is 8.848 km.
It seems to work to a first approximation. Expected height of Olympic Mons: 8.848*2.66 = 23.5 km
https://en.wikipedia.org/wiki/Mars
https://en.wikipedia.org/wiki/List_of_highest_mountains
https://en.wikipedia.org/wiki/Olympus_Mons
For fun I tried a different tack:
Geology tells us that quartzites are one the strongest rocks with a upper end compressive strength of approx. 300 MPa. The density of quartzite seems around 2800 kg/m3.
Using that as the limit at which a column of rock would cause the bottom-most rock layer to crumble under its self-weight I get a height of about 11 km.
http://www.eos.ubc.ca/ubcgif/iag/foundations/properties/density.htm
http://www.oocities.org/unforbidden_geology/rock_properties.htm
Those compressive strengths, are they for uniaxial compression? Because the rock at the base of the mountain is likely to be more like hydrostatic compression. Typically it’s hard to get a solid to fail under hydrostatic compression. Most stuff becomes “more solid” when it gets compressed.
As evident in the diagram, it’s the shearing near the edges of the domain that actually makes for the failure mechanism of interest.
Interesting. Yes, I think these are uniaxial. Even at the base wouldn’t the mountain edges fail at the uniaxial limit? There’s nothing to constrain a mountain edge from the outside to put it under hydrostatic compression. Correct?
Once failure starts at the edge it would progress progressively inwards.
Why shear? Under a strictly downwards loading without any bending moment would there be shear? I wonder how I’d estimate this shear. Any idea? Rocks seem much weaker under shear. Typical values I see are about 50 MPa max.
Uniaxial loading produces shear at 45 degrees to the loading axis. Yes, you’d see failure near the edges where this shear occurred and then as the rock failed, you’d have a complex flowing of the rock. The rock below the middle of the mountain wouldn’t do much at all.
To see what that might look like, try filling a bowl full of say rice, and then get two glasses, one a short “old fashioned” glass, and one a tall “collins” glass. Fill them both with rice to get a good weight, and then flatten the surface of the bowl of rice with your hand and put one of the cups in the middle and let go. The old-fashioned glass will likely sink in a few millimeters, but the tall collins glass will sink in farther, maybe a cm or so, and will push up the rice around the edges.
In this experiment, the “bonding” between the rice grains is just a frictional one, and so it’s much easier to break. We’ve essentially lowered the E_liq in his calculation so we can see what the response is likely to be at human scales.
This model predicts a scaling law for mountain size as a function of various parameters:
h < E_liq/(A m_p g)
On different planets, g will be different. With different materials, E_liq will be different.
How well does it work? Well, first remember it’s an order-of-magnitude estimate, so it predicts < 30km on the earth, but actual mountains are more like 9km (everest = 8.8 km)
Olympus Mons on mars is about 24km or about 2.7x as tall as Everest: g_earth/g_mars = 2.5 or so. So the scaling law seems to work for other planets, and will probably work well for other materials as well.
You make an interesting point, but I think you may be misinterpreting the intended purpose of these sorts of calculations. I (and I think most physicists) use calculations like this as a sort of filter. They belong to a class of calculations that are often referred to as “naive calculations.” The idea is that if a calculation like this gives a value that is around the same order of magnitude as the value observed in nature, then a more detailed calculation (or, more generally, investigation) probably wouldn’t reveal very much of interest (emphasis on the “probably;” we all have limited time and can’t check everything in detail, but there is always the risk that we might miss something this way). On the other hand, if the naive calculation proved to be woefully inadequate, then there is probably some interesting physics to be discovered by looking more closely at the phenomenon. A current, well-known example of this sort of filtering approach is the phenomenon of Dark Energy. Current observations put the amount of dark energy at a value that is something like 120 orders of magnitude different from the value suggested by a naive calculation based on the Standard Model of particle physics. If this were not the case, I doubt that as many theorists would be working in that area as currently are.
Of course, another use of these sorts of calculations is precisely to detect “snake oil.” If someone makes a quantitative claim (even in a field of study that I know practically nothing about), my tendency is to try to do some sort of order of magnitude calculation to see if the claim is reasonable. If the calculation agrees with the claim, then I will probably let it it pass without comment. If it doesn’t, then I will probably press the person making the claim for more details. But, really, this is just another kind of filtering. I think most physicists do this (some more tactfully than others) and it probably has a lot to do with our collective reputation for being annoying at interdisciplinary seminars.
As for the mountain height calculation, yes, it does work for other planets (you can Google for the relevant numbers to plug in). And the tallest mountain on Earth is around 8.8km high, so it is just barely the same order of magnitude as the 30 km calculated above (on a log-10 scale, 30 is almost order of magnitude 10^2). A snake oil salesman who was trying out lots of models in order to convince someone of something would probably try to get a bit closer than that. But, as I say above, that’s not really the intended purpose of these sorts of calculations.
Vicky was a legend at MIT — all of the older physics professors spoke endearing of him for insights like these. Andy, was he completely removed from the undergraduate physics experience by the time you went through? I wonder when they started transiting to the current approach, which I absolutely hated tutoring as it seemed to resort to learning computational tricks without any motivating understanding.
Mike:
I’d never heard of this guy before seeing this online book. But as a MIT physics undergrad, I had no contact with the physics dept other than taking classes. I never went to any physics events, academic or social. I did all my homework, though. Kind of an MIT thing.
I got perfect grades but never understood things very well, which is why I decided not to go to grad school in physics.
I did all my homework and study at the last minute (did also get [nearly] perfect grades though) in part coz I spent a lot of time reading interesting things in the library. I also went to uni in a country of only 4 million people.
So while I do have a lot of sympathy for frustration over how courses are taught and framed I also think people need to embrace the risks of thinking for themselves earlier. Especially if you’re getting perfect grades and/or at places like MIT. My brief experiences of teaching at Oxford indicate similar ‘get the grades’ attitudes.
My worst grade came in a course that I ran out time to study properly for coz I got too distracted by diving deeper into one of the topics and ignored the rest. Not claiming to be holier than thou, just putting it out there.
I think if I decided to be a professor of the “teaching people stuff” variety (as opposed to the kind of professor that does almost all research and little teaching) I’d probably run my classes almost like 3 parallel ones:
1) Do homework, do several midterm short tests, take a final exam, get enough points.
2) Choose from suggested projects, carry them out, explain them in write-ups, take a conceptual final exam.
3) Design your own projects, carry them out, write them up, present them as final exam.
I’d probably let people mix-and-match a little. There might be say 5 midterm short-tests on a 2-3wk rotation, but in any period you could choose to do a project instead, and/or design your own project.
I know, it’d be hard to grade, and take a lot of time, but I was a lot like ojm, always wanting to dive down a rabbit hole, but needing a little structure and support, and also needing to not fail because I spent time in the rabbit hole instead of doing textbook problems… so I feel like that’s a worthwhile thing to actually have a plan for handling.
+1
+1
I think its a tradeoff. A lot of real life situations require diving down rabbit holes you are not interested in diving down in.
Sure, I mean I still got like a B+ or something. But a lot of life is more like an open-ended project than an exam and can involve taking a risk every now and then to pursue things you believe in.
Daniel’s proposal is pretty balanced and I’m talking more about high achieving kids who are too scared to ‘fail’ ie get a B+. The whole ‘real world’ thing is often used as a scare tactic to encourage conformity. If you have the privilege of having some brains and educational opportunities, may as well do some interesting things with it too.
Yes, agreed. The other extreme of this is what I call the “special snowflake” syndrome. Some of the high achieving kids these days get it drilled into them that they are special and must only follow where their passion leads them to. There can be this disparity between what’s interesting to you and what’s useful to society. Sometimes it helps to have the discipline to do what does not seem interesting to you but is needed of you.
The irony is quite often what you thought was uninteresting & only did because you were assigned it can, given time, develop into an interesting problem that you never thought it was.
Forcing yourself to do stuff you don’t like to do, can be a very useful trait to nurture.
In any case, all I’m saying is that there’s this middle ground is between that’s probably the best spot. And hence I feel at least some projects must be assigned projects, even if open ended, where the student gets no choice about what project he works on.
Rahul: teaching undergrads at USC gave me a perspective on some of this. The best students would dive down rabbit holes with you, the average students would treat a rabbit hole like it probably had pit-vipers in it. They just wanted repeated rote doing of textbook problems as fast as possible so that they would get an A on their midterms and finals which they expected to be exactly like a homework problem.
The worst situation was the wealthy privileged students who wanted good grades even if they didn’t do well, and blamed the teacher/TA for poor performance.
Healthy levels of risk-taking behavior are something worth learning because it’s how we make progress in society. The “textbook problems for breakfast lunch and dinner” method of teaching not only doesn’t teach any kind of risk-taking, it actively discourages it.
Balance in all things.
Agree with all the above. Can’t say I’ve exactly figured out life but what little I’ve learned is pretty consistent with both of you.
A note – it also depends on what you consider valuable to society right? I can think of plenty occupations which society ‘value’ which I’m pretty dubious on the value of as compared to less well compensated jobs. So it does come back to making your own choices – and these could be as much based on ethically chosen risks as special snowflake expectations.
Andrew, you’d probably enjoy this:
https://mitpress.mit.edu/books/street-fighting-mathematics
Along the same lines (and by the same author), see
https://mitpress.mit.edu/books/art-insight-science-and-engineering
Also, Weisskopf had a series of articles (a column of sorts) in the American Journal of Physics called “A Search for Simplicity” that does more of this sort of stuff. He also had a shorter article called “Of Atoms, Mountains, and Stars: A Study in Qualitative Physics” in Science [Vol. 187, No. 4177 (Feb. 21, 1975) (pp. 605-612)] that is similar to the linked article. I use the Science article (along with a reading guide that I wrote) as a sort of multi-day culminating experience in the second semester of intro physics. It seems like a good way to drive home the gist of modern physics without having to solve PDEs (which the students aren’t equipped to do).
Right, I was recalling that he had written something somewhere that I had seen, way back when, and AJP seems like the right place. Thanks for the pointers.
My freshman physics was taught by Dr. Harold Rorschach (MIT graduate) using the Berkeley Physics volume on mechanics, supplemented by the Feynman lectures. I seem to recall the first weeks having a number of these sorts of reasoning exercises.
What sticks out even more strongly in my mind is Dr. Zevi Salsburg’s freshman chemistry course. I still remember the day he came into the lecture hall, claimed to have forgotten his notes for the day, and proceeded to derive the material of the day from first principles, complete with a dead-end or two that led to retracing his steps and more teaching. I’m pretty confident that was a pedagogical ruse, but it forever imprinted on me that one can and should be prepared to work from first principles rather than memorized procedures and formulas.
I started undergrad as a physics/math double major and even though physics uses a lot of math, as seen in this wonderful presentation, “thinking physics” is very different than “thinking math.” Even the very first step, thinking about the limits of rock strength, requires really understanding the constraints set up by physical reality, while in so much of math, a proof starts with the constraints set up by the mathematician. If you don’t like the constraints, redefine and transform! Much more difficult to do with a mountain. I was always much better with the latter mode than the former, and dropped the physics major.
It’s a good point. There’s a big difference between applied math or physics, and the kind of thing that most mathematicians do. To connect the world to a mathematical model is a creative step that many mathematicians don’t “grok” but then, once the model is in place, they can work with it and generalize it or find ways to compute with it or whatnot.
On the other hand there are a few places where Applied Math departments really exist. There’s a history of good stuff coming out of the UK. I love my small library of various Cambridge Univ. Press applied math texts (oddly often written by Oxford professors)
Full disclosure: I did a math major in college, then a second bachelors in engineering, then a PhD in engineering. I loved my math major work, but I tended to gravitate towards modeling and engineering so it made sense to move away from Math departments.
I’m reminded of Thing Explainer: Complicated Stuff in Simple Words.
The mountains is a great thing to study, but the Earth actually has solid crust of about 30-100 km deep. Part of it though is floating, which relives pressure somewhat…
Very interesting.
e.g. “Earth’s mantle is a silicate rocky shell with an average thickness of 2,886 kilometres (1,793 mi). The mantle makes up about 84% of Earth’s volume. It is predominantly solid” (Wikipedia)
So why doesn’t most the mantle liquefy due to the pressure of the mantle above it? How does Weisskopf’s calculation fit into this?
Hmm… People describe the mantle as solid, but a better way to think about it is in terms of the Deborah number, a dimensionless number that is the ratio of the duration of stress-relaxation to the duration of observation.
If you load the mantle with an earthquake shear wave (loading time ~ 1 second), it responds like a solid and propagates the shear wave, but if you crush two plates together to form the himalayas and watch the mantle underneath for a couple hundred million years (loading time 3*10^15 seconds), the mantle will respond by squishing around like jelly.
For a sort-of-human-scale example of how the Deborah number works see the “pitch drop experiment”:
https://www.youtube.com/watch?v=UZKZF7FNh_0
It’s been running for decades and only a few drops have fallen out of the funnel. But if you had a picture a day for 15 years and sped it up to play out in 5 seconds and compared it to some water with a little thickener dropping out of a funnel in real time for 5 seconds, you’d see they’re basically the same process.
But, if you try to propagate a 1Hz shear wave through the water you’d get no luck, whereas you can propagate 1Hz shear waves through asphalt without any problem.
Then there’s the Mythbusters examining this same phenomena:
https://www.youtube.com/watch?v=5GWhOLorDtw
Imagine a single crystal of quartz. Drop it into the ocean over the mariana trench. It falls through the water into the Challenger Deep (11km deep). Throughout this time it’s in a predominantly hydrostatic compression. Does it liquefy? Suppose you could find some much deeper place, like 30km, would it liquefy? (about 300MPa at that depth).
I doubt it, generally liquids are less dense (take up more volume) at a given temperature and pressure (water vs ice notwithstanding, water is weird). So liquefying at a given temp and pressure would typically involve expanding, which requires doing work against the surrounding fluid.
Now, if you have a shearing situation, then along the plane of shearing you could break bonds and have flow. It’s this breaking of bonds along a shearing plane that is really what’s going on in the calculation here.
Imagine a block of steel placed in a uniaxial compression tester machine. You crush it down vertically, what does it do? Initially, it deforms elastically, but after a certain level of stress, it deforms permanently (plastically) and the way it does this is to push out the sides of the cube where there’s no restraining pressure. Metal is flowing “like a liquid” in this situation, but it’s not liquid except maybe at the boundaries between micro-crystals within the polycrystalline solid.
Daniel:
Very interesting all this.
So is the right way to look at Weisskopf’s calculation is to think of it as a geological time scale limit on the height of a mountain? I.e. If you could just magically create a 50 km tall mountain it would stay there but over a million years slowly “liquify” at its base and flow and shrink down to a 30 km height?
Also, maybe in the context of the mantle the way the limit works is that the mantle could not have a local spike (“mountain”) of more than 30 km? That spike would liquify and even out the mantle to a rough spherical shape?
I.e. If a shape is already spherical it has attained its stable shape and even “liquification” wouldn’t change things much?
Yes, something like that. It’s all involved with flow over long time scales. If you can magically make a mountain of 50km and plop it on the earth, you’d have several processes each of which would occur on different timescales.
You’d have elastic deformation and wave generation on the shortest timescales (ie. microseconds, seconds)
You’d have crack formation and sliding along faults on slightly longer timescales (ie. milliseconds to weeks)
You’d have fault sliding / aftershocks on medium timescales (days, weeks, months, decades, millenia).
Then, you’d have melting, and plastic flow on the longest timescales (millions of years)
The mantle is actually fairly dynamic on millions of years timescale and that dynamism seems to be driven by a combination of thermal processes, bouyancy, magnetic fields, etc. The thermal stuff is driven by atomic / radioactive processes:
https://en.wikipedia.org/wiki/Mantle_plume
In hindsight, I sort of feel cheated by Weisskopf’s explanation then. It represents the equilibrium picture but the reality is that the world we all live in is mostly a kinetically controlled world.
At the time scales of human existence this 30 kilometer height limit Weisskopf derived seems entirely irrelevant.
Like you describe, I could very well plop down a 50 km tall mountain and it would stay there. True it would *eventually* sink to 30 km but that’s only over a scale of millions of years.
But, you can’t plop down a 50 km tall mountain, you have to “build it up” and in that process the calculation he gives represents a horizontal asymptote across which the dynamics can never go. So you won’t ever see a 30km mountain on the earth.
Also, for the “plop down” experiment, even if you lowered it over a period of say a year rather than dropping a 50km diameter meteor at high kinetic energy, it’d still cause violent earthquakes, cracking, deformation, and all kinds of drama on human timescales.
Often these kinds of calculations are basically taking a dynamic process and solving for some steady-state which turns a differential equation into an algebraic one. So, as long as you kind of “know” that, you won’t feel so cheated, and you can use the info properly.
I studied in the Natural Sciences school of the University of Buenos Aires in the 90s. One of the best books for the early Physics courses was the “Mecánica Elemental” from Juan Roederer. It was written in the (no idea) 70s, or so, during the so-called “Golden Era” of the University of Buenos Aires. Shortly after the Feynman lectures came out. It was hard to find and old copies were circulated among students. We also had modern books and the Feynman lectures, but the “Roederer” was a great perspective. It was clearly written, had interesting examples, and was rigorous and concise (two features that most other Physics books lacked). It also had a home-made look. It was one of my favorite books, although I never owned one. I think you can only find it in Spanish, the Internet is full of pdfs of this book, the following is a later re-edition, so it looks more like a traditional book. But the content is pretty much the same.
http://www.gasaneofisica.uns.edu.ar/fisica1/libros/roederer.pdf
This is a wonderful post — thanks! It reminds me of the similar question of what sets the maximal height of trees — that’s a tougher one, though, and more contentious, but still fascinating. As for it being “a challenge to write a statistics book of this sort,” I can assure you that it’s a challenge to think of physics problems of this sort, too!
Hi Andrew,
>it’s a challenge to write a statistics book of this sort. I’m working on it
I wish you all the best in your work. I like Freedman et al, and also Bock et al. Both books are well-written, if sometimes a little hand-wavy, due to the simplified maths. It would be nice to find a text that’s more mathematical, with a lot of personality. I wrote a recent, very negative Amazon review of Rice’s textbook. He made a huge mistake IMHO by not bringing in a collaborator who understands and values reaching the student mindset better.
I’m so sorry to have to say this, but I think you should hear it from at least one person: there’s something about the printed text in BDA3 which isn’t great (at least in my copy). Sometimes I find it visually tiresome to focus on for extended reading. I can’t put my finger on it: Maybe it’s the font? Maybe I’m perceiving lowish contrast vs. the paper color? I wish I could be more precise. I hope you might please factor in this consideration during future book planning.
I personally like the Courier family, and use it for most of my own primary technical work. I loved seeing it in this post! It reminded me of Feynman’s published “Lectures”, which IIRC from my college days were in Courier at the time. I also love that K&R “C” was written in Courier. Surely the Courier family is a non-starter nowadays. I wonder if there’s a strong contender for accepted successor?
Did anyone do or reference any survey work for BDA3, on font choice? If so, can you share any findings with us, please?
Brad:
I have no idea on fonts. That’s Bob Carpenter’s favorite topic.
People hugely underestimate the impact that fonts, page color, margins & other typesetting quirks have on the readability of a book.
Rahul,
Thank you for your supportive comment. Yes, agreed completely!
A Google search on ‘best fonts for academic writing’ presents a number of interesting links..
I found the presentation of the maximal height of mountains to be frustratingly error-prone. I always attempt to follow and verify the formulas and substitutions, and it becomes extremely annoying when the text is inconsistent, or fails to define its terms, or switches letters repeatedly, or does multiple simplifications in a single step, only to get that step slightly wrong. When any one of those mistakes happen, the clever student can recognize the error without it becoming too distracting. But if several of those things happen at the same time, it is very difficult to actually follow the logic, because you’re having to guess at what they “really” meant. And when you’re learning a subject for the first time, as opposed to seeing a new spin on already-mastered material, attempting to guess at what the professor “really” meant becomes a serious of shots in the dark.
I’m referring specifically to the text preceding and immediately following Equation (1.6). Starting with
$latex E_{\mathrm{liq}} = \beta B = \beta \eta \mathrm{Ry}$
We need to infer that $latex B$ is the binding energy discussed above, which is fine, but we also need to recognize that $latex B = \eta\,\mathrm{Ry}$. Now, it may be that $latex \eta\,\mathrm{Ry}$ was frequently used in earlier sections, and so is presented without remark here, but clearer texts would remind the reader what exactly $latex \eta\,\mathrm{Ry}$ represented—namely, the lattice energy for $latex \mathrm{SiO_2}$, given as a propotion of the Rydberg energy (the ionization energy of a hydrogen atom.) A minor typo in that line also has him writing silicon oxide, when he clearly means silicon dioxide, consistent with what comes both before and after in the text.
After that, when substituting $latex \beta B$ for $latex E_{\mathrm{liq}}$ in the equation for $latex h$, he inexplicably switches from using $latex B$ to $latex B’$.
$latex h \leq \frac{\beta B’}{A m_p g} $
To make matters worse, in the next line he swaps out $latex \beta$ for $latex B$!
$latex h \leq \frac{B \eta \mathrm{Ry}}{A m_p g}$
My guess is that, in the first draft, he used $latex B$ to be the scaling factor of 0.1, and $latex B’$ as the binding energy, and then decided to go with $latex \beta$ and $latex B$. Unfortunately, he didn’t change all of the original sets of $latex B$ and $latex B’$.
To top it off, he simplifies the constants in that equation, $latex \frac{\mathrm{Ry}}{A m_p g}$, into $latex 3 \times 10^8\;\mathrm{cm}$, which is slightly wrong (but close), and then changes it $latex 2 \times 10^8$, which is correct, but leaves off the units. And then makes yet another math error simplifying to the next line: $latex \frac{1}{10} \cdot \frac{1}{5} \cdot 2 \cdot 10^8\;\mathrm{cm} = 40\;\mathrm{km}$ not $latex 30\;\mathrm{km}$.
Even if there were no mistakes, I think exploring concepts in this way is interesting, but not of much educational value to the new student. There is simply no way to come up with the sorts of reasonable approximations that he used without a large breadth of knowledge and experience.
*series, not serious
I had the same observations working through the example — the notational lapses around eq. 1.6 are especially annoying — but as I started to write, I realized that this would be a very long comment. As noted above, I love examples like this. However, it is very clear if one actually tries teaching this sort of thing that (i) the style of thinking it exemplifies is very non-obvious to most people, even most science students, and (ii) seeing or reading an exposition like this doesn’t do much to teach this style of thinking. Instead, actually working out the logic oneself is crucial. This is, of course, true for learning most things, but it’s especially true here. Given this, the errors and “sloppiness” that are found in this example are part of the experience of figuring it out. I could imagine asking students to study this, and to write a “cleaned up” / critiqued version. There’s more to write, but I’ll stop now…
On a similar note, here’s nice popular lecture in which Lawrence Krauss shows the power of order-of-magnitude estimates by assuming that cows are spheres :)
http://www.youtube.com/watch?v=LTie-g0xNQ8