I’m posting this one in the evening because I know some people just hate when I write about plagiarism. But this one is so ridiculous I had to share it with you.
John Smith (or maybe I should say “John Smith”?) writes:
Today on a political science forum I saw this information about plagiarism by two well-known political scientists (Jon Hurwitz and Mark Peffley). It checks out, and I thought you might be interested.
The 2010 article below is just a verbatim combination of the 2005 and 2007 articles. It has the same data, findings, tables and figures as the 2005 and 2007 articles, and it shares a lot of the text too.
For example, table 1 (p. 466) in the 2010 article is identical to the first part of table 1a on p. 772 of the 2005 article. Figure 2 in the 2010 article is identical to figure 1a on p. 774 of the 2005 article.
Figure 1 (p. 1006) in the 2007 article is identical to figure 3 (p. 471) in the 2010 article, except that the x-axis is labeled differently. Table 2 (p. 1004) in the 2007 article is identical to table 3 (p. 470) in the 2010 article, except the control variables are not shown (but are included) in the 2010 article and one of the six coefficients in the 2010 article is different (.03 versus .01). Table 1 (p. 1002) in the 2007 article is identical to table 2 (p. 469) in the 2010 article, but uses a different rounding scheme and adds the question text.
Hurwitz, Jon, and Mark Peffley. 2005. Explaining the great divide: Perceptions of fairness in the U.S. criminal justice system. Journal of Politics, 67(3), 762-83.
Peffley, Mark, and Jon Hurwitz. 2007. Persuasion and resistance: Race and the death penalty in America. American Journal of Political Science, 51(4): 996-1012.
Hurwitz, Jon, and Mark Peffley. 2010. And justice for some: Race, crime, and punishment in the US criminal justice system. Canadian Journal of Political Science, 43(2): 457-479.
My first thought ways: Hey, they’re 3/5 of the way towards satisfying Arrow’s theorem. But I don’t know anything about the Canadian Journal of Political Science: maybe they publish review articles? Anyway, I’ve been known to copy my own material from one article to another so I can hardly criticize others for doing so.
So I took a look at the 2010 article, and . . . they don’t cite the 2005 and 2007 papers at all! Here are the relevant section of the references:


Hmmm . . . now I better check. Did they really cut and paste from their previously published material? Yup.
From the 2007 article:
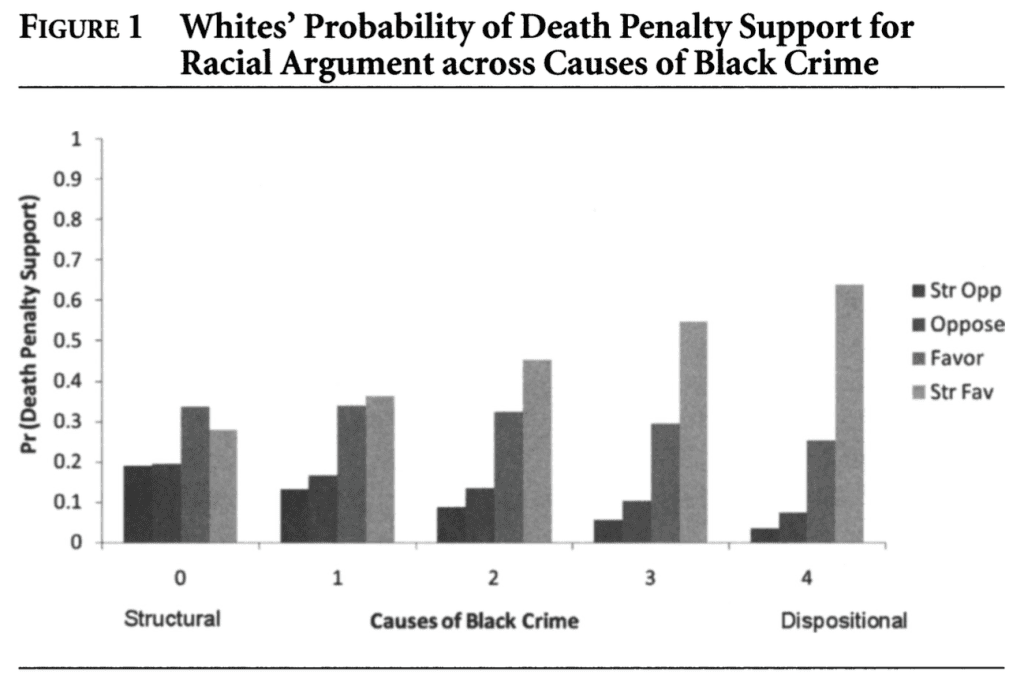
And again in 2010:
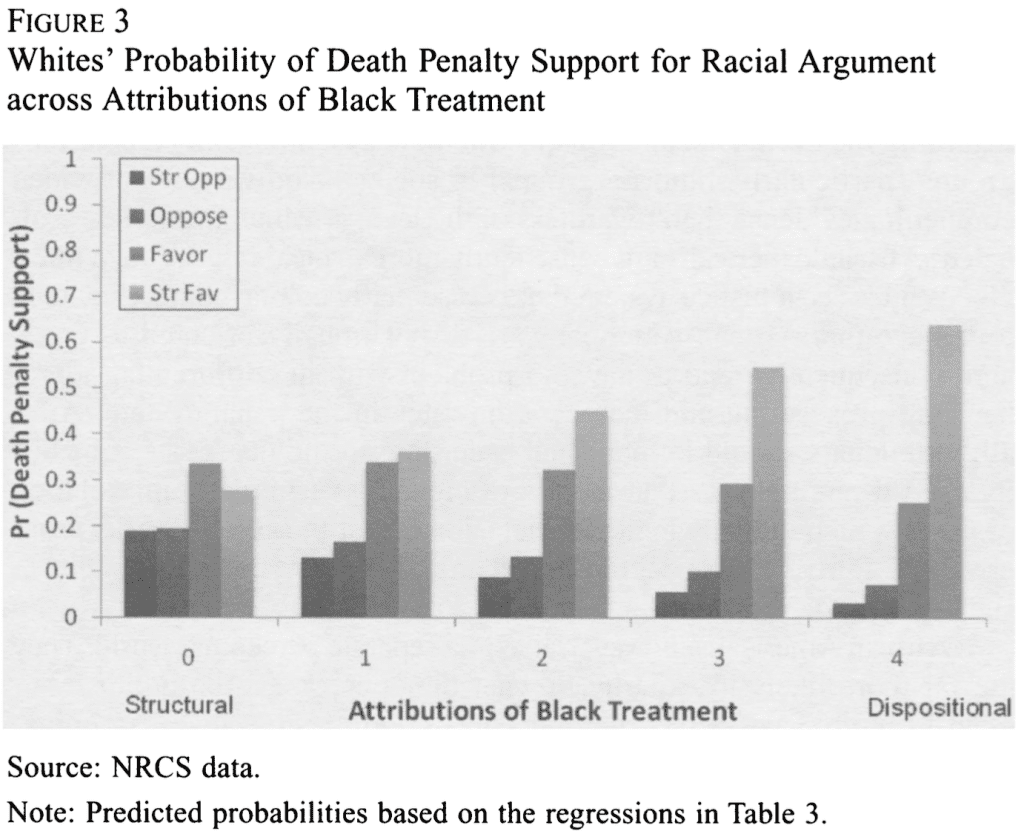
Same blurry figure. What did they do, scan it in from the newspaper or something?
Say what you want about Michael Lacour, at least he knew how to make a pretty graph. These guys are such amateurs.
Oooh, sooooo tacky. If you think your work is so great that it should be published in multiple journals: fine, go for it (unless of course the journal submission requires you to attest that no part of this work is published elsewhere). But own your choices, for chrissake. Not citing your own AJPS paper where you took your graph . . . that’s really bad news.
I’d hate to be a student in one of these guy’s classes.
I googled *Mark Peffley syllabus* and found this:
A “critical literature review” or “original research.” But not both.
P.S. Just to head off any comments on this point: I’m not not not saying that all published papers should have original research. Review articles are fine. It’s fine to copy figures too: maybe certain pieces of news that were published in AJPS have not made it over the Canadian border so let’s share these findings with our colder cousins. What I hate here is the dishonesty: not citing the earlier published work and thus implying these were new findings. Again, if Hurwitz and Peffley wanted to republish their figures, that’s fine with me—but obviously they thought it wouldn’t be fine with someone else, so they covered their traces. The lack of references to the earlier papers, that’s the smoking gun.
P.P.S. I have no comment on the research itself. Literally no comment: I’m not expressing a positive or negative view—it could be great stuff, perhaps so wonderful that it deserved to be published three times. I did not read the articles, I just looked at them enough to check that there was indeed copying.

Every time someone in Poli Sci or Psych commits these stupid antics it diverts useful resources from detecting fraud in the places that really matter: e.g. Clinical Trials.
Maybe if all the Hurwitz-es and Peffley-es & LaCours behaved, it would give Andrew etc. more resources to focus on the bad pharma stuff.
Rahul:
Interesting point. It reminds me of my criticism of Don Rubin for consulting for cigarette companies. Not that it’s immoral of him to work for them (who knows? It’s not my call) but that it diverted him from more important topics.
Random thought: How about if you self declared a moratorium on certain subject areas. Would that refocus your attention on different domains?
e.g. The crap in Psych. & Poli Sci. you’ve spent lots & lots of time on so far.
Perhaps, you’d next discover a can of statistical worms in CERN-LHC results or at NASA or in Quantum Computing or something? That’d be fun.
PS. New tag suggestion: “Can of statistical Worms”
I don’t know about the work at CERN, but the main paper accompanying yesterday’s Gravity wave announcement (Abbot et al, PRL 116, 061102 (2016)), uses terms like “90% credible interval” and “Bayesian inference.” I can’t find a P-value anywhere, although they do calculate a “false alarm probability” which seems similar to a P-value. But, they get a value of about 10 to the minus seventh power for this quantity.
Of course, perhaps they could be criticized for using LALInference rather than STAN.
These people seem to do signal processing and probabilistic reasoning in a different league than do the psychology publications that Andrew addresses from time to time.
Consider that people’s lives are more likely to affected by an individual, physician or bureaucrat relying on a bad psych study than by an error in the estimation of the masses of two black holes that merged a billion years ago. So, I vote for Andrew to stay the course—it’s a target rich environment and improvements in the quality of research in those fields may make people better off.
That said, I would prefer that the heading to this post not contain the adjective “Sleazy-ass”, but it’s his blog, not mine. I don’t have to read it.
Bob
Do you believe this 10 to the minus seventh power false alarm probability?
I haven’t gone through their calculation but intuitively Sounds a tad far fetched to me.
Well, 10 to the minus seventh is pretty low. But, recall that the event was observed by device in Louisiana and was observed by the device 1,800 (0.010 light seconds) miles away in Washington state 7 ms later. You can see the structure of the detected waveform in the band-pass filtered data.
My reaction is not to just one number, but the whole presentation of their analysis. For example, they calculated several different “P-Values” for their observations (5.1 sigma, 4.6 sigma, 4.4 sigma)—depending on how they structured their search for events.
The description of the system is mind-boggling. To calibrate the measurements, they shine a light on the suspended masses and measure how the masses move. There is 100 kW of light in the cavity. The system reduces vibrations the measurement system caused by ground motion by 10 orders of magnitude (100 dB). Pressure in the cavity is less than 1 micro pascal (1.4 E-10 PSI).
My fear is that to credibly give a false alarm probability so low you must look into all kinds of 2nd order impacts like hacking, malfeasance etc.
e.g. Say, a conspiracy theory, which in normal circumstances I would laugh away, must be considered when you assign probabilities that low.
Almost any odd, improbable fact becomes grossly highly likely in comparison when your baseline probability is so low.
Rahul: if you set up an experiment to observe something, and you find what you’re looking for, and you can calculate that it would happen by chance once in one million years, that’s very interesting. If you observe something (like their second most significant event) that you would expect to see every couple of years by chance, that’s not so interesting (and it would not be on the news). Reporting five-sigma events is usual in particle physics.
Nobody says that 10^-7 is the probability of this announcement not being the first direct detection of gravitational waves. Maybe gravitational waves don’t exists and they were just lucky or observed something else, maybe they made up the results, maybe there is an error somewhere in their calculations. But it’s not unreasonable to conclude, tentatively as always in science, that they have observed the merger of two black holes. It’s not like they are claiming to have proven ESP or the discovery of a magnetic monopole.
> “I can’t find a P-value anywhere, although they do calculate a “false alarm probability” which seems similar to a P-value. But, they get a value of about 10 to the minus seventh power for this quantity.”
I was extremely interested to see the reasoning used in this paper. They do use p-values but call it “significance”:
“The significance of a candidate event is determined by the search background—the rate at which detector noise produces events with a detection-statistic value equal to or higher than the candidate event.”
As the paper goes on the term “false alarm rate” morphs into “false alarm probability”, and by reading between the lines you can see they were always interpreting it this way. This the common fallacy that the p-value is the probability of a false positive. This is wrong because if events that produce detectable gravitational waves of this type are extremely rare, it may be very probable this is a false positive signal.
The strength of their claim of gravitational waves is actually determined by their ability to fit the signal with a theoretical model, and how well they ruled out other explanations: “Exhaustive investigations of instrumental and environmental disturbances were performed, giving no evidence to suggest that GW150914 could be an instrumental artifact [69]”
That they are unlikely to get such a signal according to the background model is just a minor aspect of everything discussed in the ref 69 sister paper. They give it inappropriate focus only because of “the p-value is the false positive rate” fallacy mentioned above.
> As the paper goes on the term “false alarm rate” morphs into “false alarm probability”, and by reading between the lines you can see they were always interpreting it this way. This the common fallacy that the p-value is the probability of a false positive.
As far as I can see they distinguish the “false alarm rate” (one event per so many years) and the “false alarm probability” (probability of getting at least one event over the duration of the experiment).
I don’t understand why do you think that they are misinterpreting their significance calculations as a false positive rate.
“[…] false alarm rate is lower than 1 in 22500 years. This corresponds to a probability < 2 x 10^-6 of observing one or more noise events as strong as GW150914 during the analysis time, equivalent to 4.6 sigma."
"[…] false alarm rate for GW150914 of 1 in 8400 years. This corresponds to a false alarm probability of 5 x 10^-6 equivalent to 4.4 sigma."
"[…] an upper bound can be placed on its false alarm rate. Across the three classes this bound is 1 in 203000 years. This translates to a false alarm probability < 2 x 10^-7, corresponding to 5.1 sigma."
"[…] the second most significant event has a false alarm rate of 1 per 2.3 years and corresponding Poissonian false alarm rate of 0.02."
Yes, thanks. I see now that “false alarm probability” has a technical meaning different from the “probability the signal is a false alarm” which is what I am concerned with:
“The probability of finding the value S or more among M independent measurements, also a p-value, is referred to as the “false alarm probability” (Scargle, 1982)”
http://arxiv.org/pdf/1006.0546
So my remaining argument is that I think you would need to be insane to go through all this effort to get a “false alarm probability” and not attempt performing the next step and estimating the “probability the signal is a false alarm”.
I looked closer at these calculations. They write:
“We present the analysis of 16 days of coincident observations between the two LIGO detectors from September 12 to October 20, 2015. This is a subset of the data from Advanced LIGO’s first observational period that ended on January 12, 2016.”
We see “false alarm rate” of (1/22,500)*(16/365)~ 2e-6 “false alarm probability”, etc. The duration of the experiment was 85 days and apparently about 81% of the data was missing or needed to be “vetoed” because it was problematic in some way (leaving 16 days worth). First we should note that, as I have calculated here it at least, this “probability” is an approximation that only works if rate*duration is small. It is going to get less and less accurate and eventually rise above one when the duration of the experiment gets long enough. However, that doesn’t seem to be an issue for these values.
The preferred explanation for this signal is apparently a binary black hole merger. So we want to know what the probability is of detecting one of these in those 16 days. The rate of detections (R_d) can be estimated by multiplying rate of occurrence (R_o) by experiment duration (D), proportion of time detector is collecting useable data (P_a), and proportion of detections that don’t get filtered out for some other reason (P_x)
R_d = R_o * D * P_a * P_x
Just as a back of the napkin calculation, lets use the upper bound estimate of 3.3e-7 mergers per Mpc^3 per year and maximum possible sensitivity (in terms of distance from earth) of 500 Mpc) from this 2013 paper:
http://link.aps.org/doi/10.1103/PhysRevD.87.022002
R_o = 3.3e-7*500 = 1.65e-4
D= 85/365 = .233
P_a = .19
P_x = ??? = 1
R_d = 7.3e-6 detections per experiment.
Note that R_d is an approximation of the “probability of detecting a true binary black hole merger” during this experiment. Since we have detected a signal, it seems the odds may be as high as about 7.3e-6/2e-6 = 3.65/1 that this was a real detection rather than a false positive. This is just back of the napkin and may be way off! For example, it is not clear to me whether I should be using R_o = 3.3e-7 * 4/3*pi*500^3
They need some calculation like that, or else I do not understand their obsession with talking about the “false alarm probability”, it just isn’t very useful. Since that calculation is missing, I believe there is no way that this “false alarm probability” has been interpreted correctly.
> First we should note that, as I have calculated here it at least, this “probability” is an approximation that only works if rate*duration is small.
I’ve not done the calculation myself, but this is probably the reason why they specify that “the second most significant event has a false alarm rate of 1 per 2.3 years and corresponding *Poissonian* false alarm probability of 0.02.”
> R_o = 3.3e-7*500 = 1.65e-4 [] This is just back of the napkin and may be way off! For example, it is not clear to me whether I should be using R_o = 3.3e-7 * 4/3*pi*500^3
You are off by several orders of magnitude. It would be truly remarkable if they had established that the detectable events happen less than once in 6000 years (your first estimate) after running the experiment for sixteen months. I don’t know about the 4/3 pi, but you need the cube of the length for dimensional consistency.
> Since that calculation is missing, I believe there is no way that this “false alarm probability” has been interpreted correctly.
Why do you think it has been interpreted incorrectly? Do you see any interpretation in the paper?
>”Why do you think it has been interpreted incorrectly?
As explained above, they do not go on to use this detailed account of “false alarm probability” to estimate the probability of interest (“the probability the signal is a false positive”), despite devoting a lot of space to it.
>”Do you see any interpretation in the paper?”
Nope, there are just many paragraphs about it followed by: “When an event is confidently identified as a real gravitational-wave signal, as for GW150914…”
Suddenly it is “confidently identified”, why? As I said originally, I think this is fine based on ruling out other explanations and ability to fit the signal with theory. The false alarm probability is just a minor aspect of the former.
There is no justification offered for why we should care so much about how likely a signal would be if a building in Hanford, WA was 15 ms in the future relative to a building in Livingston, LA. It gives an idea of the background level of spurious correlations, ok… Now if they want to use that to estimate the probability the signal is a false positive, different story.
Maybe not that important which canvas you paint which scene on (except perhaps not water colours as too easy to wash away) – it should all help.
Pharma stuff has subtle clinical context that can complicate things enormously.
Yes, and that’s why we need the smartest guys to look at it. Nudge nudge Andrew.
And the relevant website seems to have changed the name of the thread to:
http://www.poliscirumors.com/topic/is-publishing-the-same-article-twice-okay
When before it was :
http://www.poliscirumors.com/topic/jon-hurwitz-and-mark-peffley-busted-for-self-plagiarism
Like the p-hacking that is your more usual topic, this sort of recycling is clearly the product of pressures to publish, together with lax editorial standards. So, if your role is to referee the game of academic publishing, fine to call foul in both sorts of cases. But is there any harm from this foul beyond reducing the reliablilty of publication counts as a form of academic scorekeeping? Not worth mentioning, really, compared with your usual topics.
Is there any harm in counterfeiting currency beyond reducing the reliability of cash reserves as a form of pecuniary scorekeeping?
What is the forgery of forged money called?
harms meta-analyses
At the end of the day how different is this from one of the most standard publication padding things political scientists do all the time: write a dissertation, turn the main argument of that dissertation into a paper, publish that at a top journal, then publish a book that is basically just the same paper again stretched out, then get invited to write in two edited volumes on the same general topic and publish chapters that are just recitations of the same exact argument as paper/book. Now you have 3-5 unique lines on your cv from the same exact work. Is this equally bad? Because this would account for easily 50% of the comparative politics faculty at most top poli sci departments.
I’ve also seen some methods people take the same methods paper and publish in a stats journal, a poli sci journal, and a psych or sociology journal, with only very slight permutations to the writing. Is that equally bad?
Lewis55:
This case seems particularly bad to me because they didn’t cite the papers from which they copied the material. That seems to me to be evidence that they were trying to cover their traces and mislead the reviewers and editors of the Canadian Journal of Political Science. If I was an editor of that journal, I’d be really mad right now.
luckily, Canadians are not know for getting really mad.
Amateurs
http://wah-realitycheck.blogspot.com/2008/09/khilyuk-and-chilingar.html
http://wah-realitycheck.blogspot.com/2009/07/oops-they-did-it-again.html