Leonardo Egidi writes:
Inspired by your world cup model I fitted in Stan a model for the Euro Cup which start today, with two Poisson distributions for the goals scored at every match by the two teams (perfect prediction for the first match!).
Here’s the model, and here are the (point) predictions:
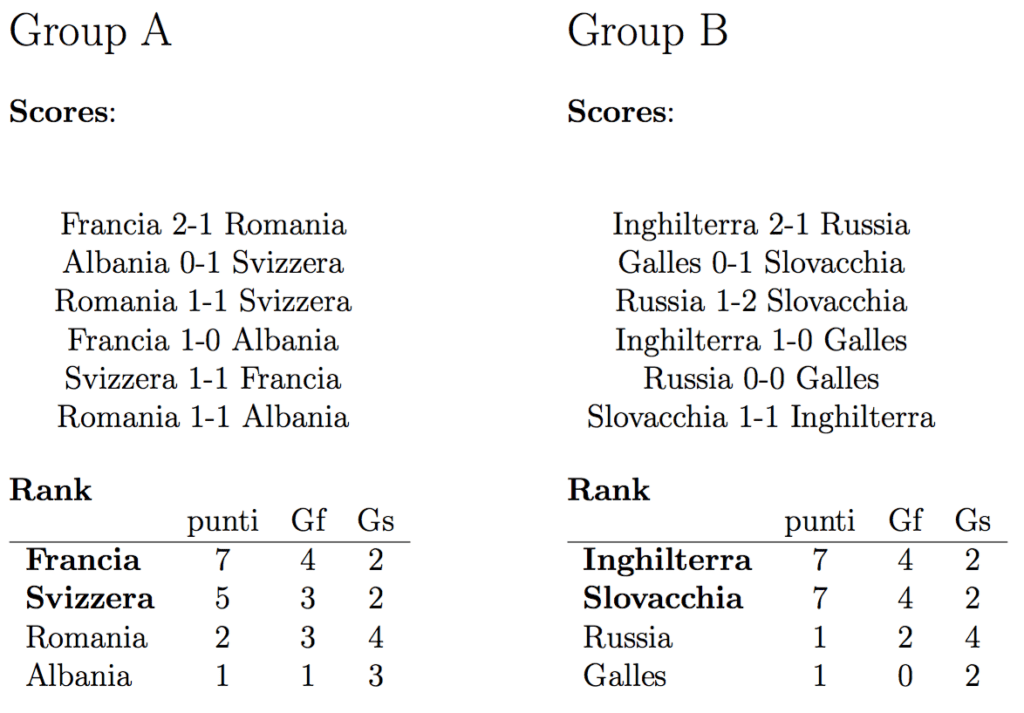
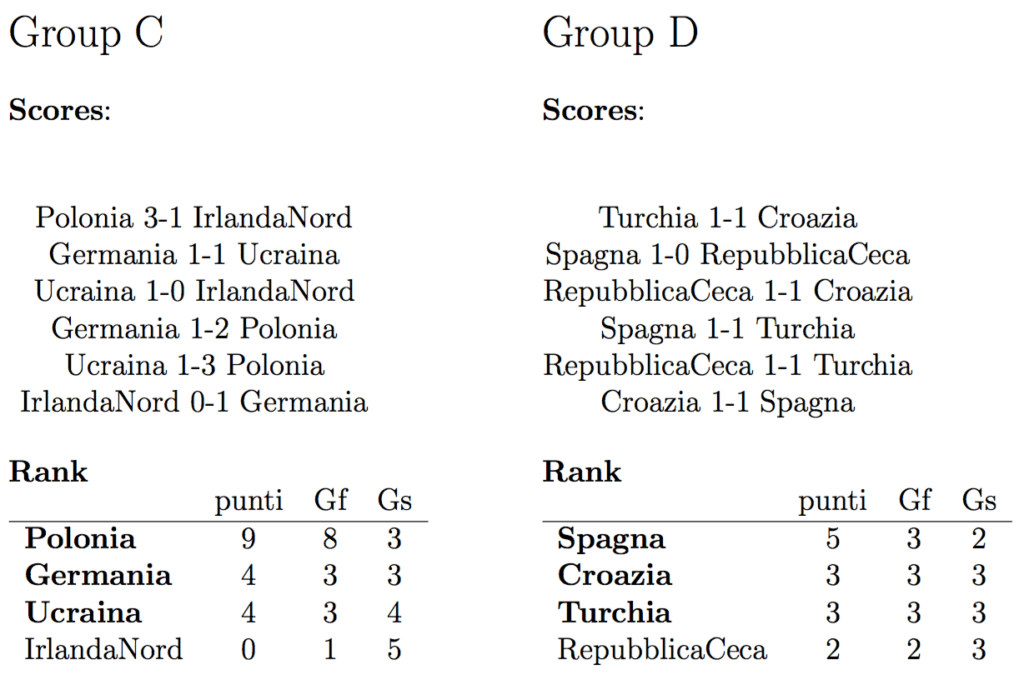
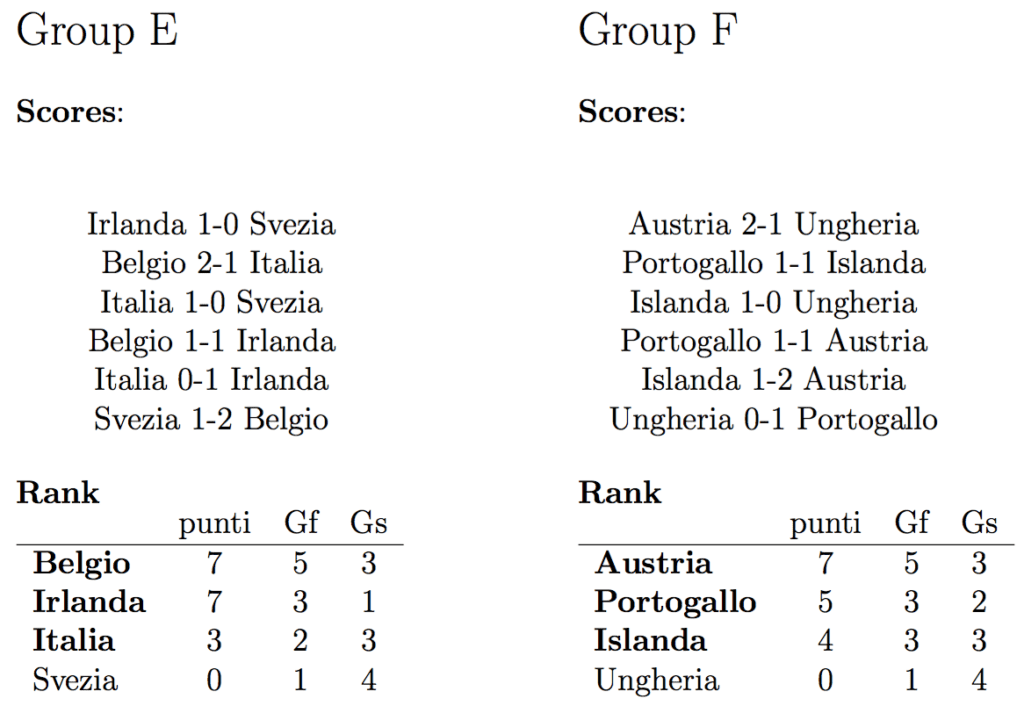

I didn’t look at the model but at first glance I think the priors are a bit vague. Maybe it doesn’t really matter, though. Anyway, I’m glad to see that France will make it to the semifinals. (I root for France whenever the U.S. and Guatemala aren’t in the picture.)
Maybe Leo can also send along the Stan code and the data?
P.S. Just to be clear: this is not my model. Leo gets all the credit/blame.
P.P.S. Leo sent me the data and code along with the following note:
I would like to re-estimate the model for the second stage of the euro cup after the first groups results.
In euro2016.R I inserted some comments for explaining my choices. I just need to point out the following:
– The “final” model I used is euro2016Matt.stan. Here I am using some – let me say – informative priors for parameters c and d which regard the attack and the defense score. By soccer experience, I notice that over the years the best teams are likely to perform quite well in the first matches, and that is the reason for my priors with a lower bound of 0.5.
– As pointed out by someone of your readers – I already answered in your blog – there is no a system yet for deciding the winner after the regular time. Quite now, the predictions for the second stage are less reliable.
What I wanna know: What does “dtr” mean. Is he suggesting England will win the Euros? If so, low face validity.
I think it simply means “at the end of regular time”
O.k., but he seems to have some way of predicting which team goes through if there’s a draw at the knockout stage. That’s not shown. My best guess is that the number of goals is rounded to the next integer and the team with the higher exact number goes through. Or is there some extra model for extra time and penalties?
I suppose the score is just a summary of the posterior Predictive density for y_m. If you take the mode or the median you got a round value, since it is generated from a Poisson distribution. I would try to generate from a Bernoulli whose probability is a function of the ratio between posterior samples of theta_1 and theta_2, such as the inverse-logit or probit.. as for the extra-time model I don’t know anything more
Andrew:
As Lemmus says, it’s difficult to buy these results at face value, but we’ll see. Out of curiosity, why are you rooting for France? This French reader appreciates your support. Allez les Bleus. :)
I’ll try and back all the match winners and correct scores in the group matches on Betfair. Shame to have missed the first one!
David:
I’d check the model a bit first before betting on it! Bayes is great but it’s only as good as its inputs.
No worries, I won’t be breaking the bank, just following for fun.
way too many draws as of quarter final. The maximum until now was 1996 with 4 draws. The model predicts 11!
England winning a shootout in a major tournament not once, not twice, but three times! Beating Germany in a semifinal! Cue the English fans seething at that sick joke.
Pending code review, I’d say fitting independent Poisson distributions is a simple but odd choice. It’s not quite as obvious as hockey’s empty netters but I should think a lot of goals happen in the last 5-15 mins of a game as the trailing side takes more risks.
I think I would try something along the lines of a Markov process and each tranch of n minutes each team has a prob of scoring dependent on the teams’ relative ranking (proxied by bookies’ odds), current score or just trailing/leading/tied, how many players each team has left.
Maybe that would match the # of draws better.
Albania 0-1 Switzerland
That’s two out of two.
As a Swiss, I’m happy to see that my country complied with the model ;)
Hi everyone, I am the guy of the model. Before of all thank you Andrew for the space, today I am travelling to Italy but I should be able (maybe in the evening) to provide you code and data, so you can check.
Briefly I answer: my original idea was to fit the model just for groups and then to use the data for groups for predicting the results from the Round of 16 to the final. Hence, predictions for the second stage of the Euro Cup are in my opinion less reliable now, and should be updated.
LemmusLemmus:
“What I wanna know: What does “dtr” mean. Is he suggesting England will win the Euros? If so, low face validity.What I wanna know: What does “dtr” mean. Is he suggesting England will win the Euros? If so, low face validity.”
yes, “dtr” means “at the end of regular time”. Sorry, I am italian and i didn’t translate that expression. And so far there is no a particoular model for predicting.
“O.k., but he seems to have some way of predicting which team goes through if there’s a draw at the knockout stage. That’s not shown. My best guess is that the number of goals is rounded to the next integer and the team with the higher exact number goes through. Or is there some extra model for extra time and penalties?”
Yes, so far it is, you get it.
Taips: great suggestion. Anyway the model for the goals I have used is an adaptation to the model used by Baio and Blangiardo (2008) and Dixon & Coles (1997). In my opinion, these kind of models don’t take care of a suitable amount of shrinkage, even if a mixture model for the group-levels parameter is used.
Thank you for your questions and your curiosity, I will be back as soon as possible with new updates.
In the comment before, the sentence
“And so far there is no a particoular model for predicting.”
should be
“And so far there is no a particoular model for predicting the outcome after regular time”
As in other fields, modeling is either retrospective or prospective. Here we are concerned with the last kind which is more venturous than the first one especially as the UEFA-Euro competition is made of two steps: i) a round robin of 24 teams distributed into 6 groups and ii) a classical knock out involving 16 teams qualified from the previous step. Incidentally, planning 6 groups of 24 teams was not the best design to get there. To that respect, I would be inclined
1)To give predictions in probability rather than pointing to a single event so that people can feel the degree of uncertainty in which we are;
2)To touch the knock out competition only when the results of the group stage are known.
In all that, whatever is the model, the big issue is on how to handle the historical data. There are plenty of them, coming from different times, at different levels of competition, with different players and coaches, either elementary or as summary statistics (at least 4 rating and ranking systems). Here lies the art of the statistician and fan of soccer to choose and digest all this stuff. The Bayesian approach may be of some help to him for doing that coherently. For more details you may have a look at.
https://www.researchgate.net/profile/Jean-louis_FOULLEY/contributions
Hi,
i tried to re-run your code and got:
Exception thrown at line 53: student_t_log: Scale parameter is 0, but must be > 0! 1
Do you know what’s going on? Great post by the way.
Alex: Hi, yeah, this is a Stan warning, and sometimes happens. But not if you run the euro2016Matt.stan, which is the final model I used, and where no student_t are used.
I suppose you could have found this issue by running the euro2016.stan, right? According to this model – the first one I fitted – the random effects are distributed as t_student. Stan has a proper way of defining truncations and upper/lower limits, in fact I defined the standard deviations coefficient in the parameters block as:
real sigma_att;
real sigma_def;
which is a common way of defining them. And, as you can see, the value 0 for the standard deviations is possible, even if not statistically plausible.
Anyway, this allows Stan to run and producing its estimates. However I am not the most expert for answering this technical question about Stan, and you could find further explanations on the Stan Google group.
Alex:
sorry, I wanted to say:
real sigma_att;
real sigma_def;
To Jean-Louis FOULLEY:
“In all that, whatever is the model, the big issue is on how to handle the historical data. There are plenty of them, coming from different times, at different levels of competition, with different players and coaches, either elementary or as summary statistics (at least 4 rating and ranking systems). Here lies the art of the statistician and fan of soccer to choose and digest all this stuff. The Bayesian approach may be of some help to him for doing that coherently. For more details you may have a look at.”
I like this your observation a lot, I agree. In my modest opinion, I am quite skeptical in taking historical data which refer to the previous world cup or the previous euro cup, which are far from the current time and current matches we wanna predict. However, a lot of prediction model for these competitions (see the model of Goldman Sachs) take these values. I decided just to take data regarding the years 2014-2016, and just the match where two teams among the 24 qualified teams are involved (I mean, I am not taking as predictors the 7 goals that Spain had scored against a minor team as Far Oer, or Azeirbaijian).
Let me know if you have further considerations, about this, or about something else.
I would just like to register my disappointment in how much more coverage the Euros are getting than Copa America.
Can we get a Copa America model, fit on data from before the tournament, to predict the probability that Brazil was going to crash out of the group stages? Bet the odds weren’t quite 5000-1, but big.
Also, I’m now curious as to what fraction of the time it is actually “better” to finish second in your group because the winner of your opposing group in the first knockout stage is not as good a team as the runner-up. I mean, I’d rather be going up against Peru than Ecuador. In our case we didn’t know that would happen (we thought we’d be avoiding Brazil by winning), but now I want to know how often that happens. Less than half the time, but maybe not a ton less.
USA!
To Leonardo Egidi,
I agree with you that individual team strength information from the previous world cup (2014) or previous EURO (2012) was too far away. But some parameters of the model such as the variability among teams entering the competition might ne more stable. On the other hand, you might concoct your own rating system based on the existing ones and expert evaluations using different statistical devices. In any case, forecasting the outcomes of the first (12 or 24) matches of the group stage are a real challenge to the statisticians and other experts. To me there is what I call the curse of the 50p. cent accuracy in predicting such soccer results (value I regularly observed for such competitions as EURO, World Cup and Championsleague. If you are doing much better, let it me know.
Jean-Louis:
Good point on using prior information for hyperparameters.
To Jean-Louis: thank you for your suggestions!
Quite now, six exact results predicted in 14 matches, not bad.
Leo, as I said when we talked at ISBA, what’s interesting (over and above predictive the median result) is to actually characterise the full uncertainty around your output. So for example, when we were doing the predictions for the WC in 2014, we got some results that we didn’t predict (eg Ecuador-Switzerland — see https://gianlubaio.blogspot.co.uk/2014/06/the-oracle-4.html), but we were indeed closer than it looks at face value, when you consider the full picture characterised by the whole joint posterior of the number of goals scored by the two teams…
Hi Gianluca, yes thanks again for your great advice. I read your blog post and I found it really interesting and helpful for my purpose. Hence I am working on my previous model for embracing this new feature.
Glad of hear new suggestions from you when I will have this extended framework.