Andrew Hacker writes:
I have the class prepare a report on how many households in the United States have telephones, land and cell. After studying census data, they focus on two: Connecticut and Arkansas, with respective ownerships of 98.9 percent and 94.6 percent. They are told they have to choose one of the following charts to represent the numbers, and defend their choice.
The first chart suggests a much bigger difference, but is misleading because the bars are arbitrarily scaled to exaggerate that difference.
I hate to see this sort of thing in the New York Times. Millions of people read the Times, it’s an authoritative news source, and this is not the graphics advice they should be given.
Let me break this down. The first thing is that it’s a bit ridiculous to make this big graph for just 2 data points. Why not map all 50 states, why just graph two of them?
The second thing is . . . hey, be numerate here! 98.9% and 94.6% look really close. Let’s ask what percentage of households in each state don’t have phone ownership. When X is close to 1, look at 1 – X. Then you get 2.1% and 5.4%, which indeed are very different.
P.S. Hacker also writes this:
In the real world, we constantly settle for estimates, whereas mathematics — see the SAT — demands that you get the answer precisely right.
Ummm, no. The SAT is a multiple-choice test so of course you have to get the answer precisely right. That’s true of the reading questions on the SAT too, but nobody would say that reading demands that you get the answer precisely right. He’s confusing the underlying subject with the measuring instrument!
Speaking more generally of mathematics: of course there are lots of mathematical results on estimation and approximation. I mean, sure, yeah, I think I see what Hacker’s getting at, but I’d prefer if he were to say that there is a mathematics of estimation and approximation, and that this is an important part of studying the real world.
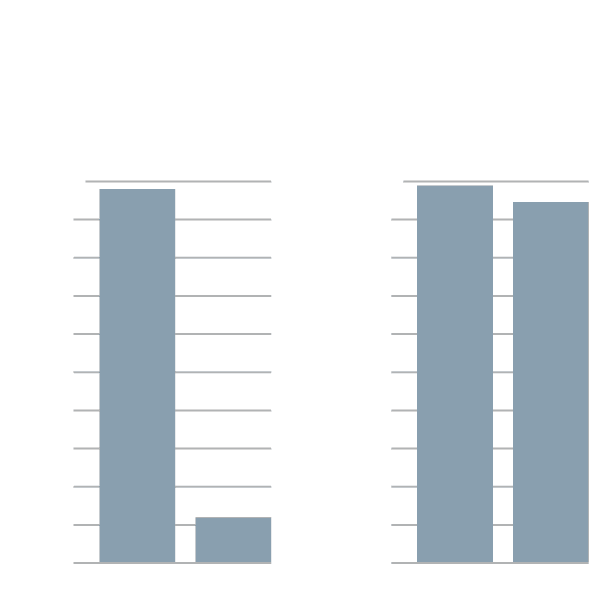
I too am constantly annoyed by this advice, which appears in many books and articles on graphics. Suppose there were almost no variability among the states, except that Arkansas was much lower than the others. Then the graph showing a large disparity might better convey the truth of the data. Assuming that 0 is always a necessary reference point is an assumption that is often wrong.
Chris:
Yes, bad practice is annoying, but bad advice is even worse. There’s something particularly grating about someone telling you what to do, when they’re getting it wrong themselves.
“He’s confusing the underlying subject with the measuring instrument!”
It’s astounding how often this happens. I sat in a room just yesterday with a group of experts who agreed on a measurement, but argued loudly about what the measurement is actually trying to measure!
> mathematics of estimation and approximation, and that this is an important part of studying the real world.
But if you confuse the two (mathematics and the real world) people have a right to laugh at you https://www.youtube.com/watch?v=r2XkfBWSmcs
This is a good piece on some of the problems with Hacker http://devlinsangle.blogspot.com/2016/03/the-math-myth-that-permeates-math-myth.html
Of course he is not alone on the start with 0 question, which is ridiculous but at the same time good to think about when you are making a graph. But don’t you think that it’s interesting how we perceive 2% and 5% as very different but 99% and 95% as not? This is why I get annoyed with some of the numeracy people when they focus on the importance of percentage change and then apply them to percents.
Funny that it puts your gravatar without your name, not sure where the name went though.
Elin:
I guess the problem here is not with Hacker, who is presumably doing his best, but with the NYT, which chooses to run an op-ed on math education written by a retired political science professor.
Devlin’s article leaves me with the impression that Hacker couldn’t tell hyperbole from a hyperbola.
“….. hey, be numerate here! 98.9% and 94.6% look really close.”
….and also be instantly skeptical that Census data has a tenth-of-one-percent accuracy.
General margin of error in Census survey data gotta be at least a couple of percent.
The Census long-form data samples about 1 in 6 households, versus short form. The Census Bureau never published margins of error with the tabular data from the decennial census. The related American Community Survey (ACS) is published annually and augments the main Census 10-year cycle. But these are basically population surveys with all the usual sources of error present; non-response rates are a significant problem in some geographical areas. The ACS is particularly noisy. Self-Reported survey data is always questionable.
And plenty of Google hits for Graphics-Editors at NYTimes, for reference.
Possible typo in post: “2.1%” should be “1.1%,” right?
You write that, “when X is close to 1, look at 1 – X.” I like this perspective. Phone “non-ownership” is five times higher in Arkansas than in Connecticut. That sounds dramatic. But that “five times” figure has a much higher relative standard error, right? Intuitively that denominator is very wiggly in the vicinity of zero. I feel like the reader would walk away from the graph with a better sense of phone ownership in the two states—and the precision of our estimates—if we show them the two boring, almost identical-looking bars. As you say, this example is a little strange because there are just two states. So that may be throwing off my intuition here.
Hacker also seems confused about the purpose of AP statistics. He criticizes the classes for not covering “citizen statistics.” That’s a worthwhile goal in another context, but the primary objective of AP is to allow students to test out of college courses, particularly PREREQUISITE courses. (I actually prefer CLEP for this, but that’s a subject for another day.) This is especially true with classes like AP Stat and AP Calc. Topics like “binomial random variables, least-square regression lines, pooled sample standard errors” are covered because the students who passed the test will being going directly into classes that require mastery of these concepts.
Yes, that was the most idiotic part of Hacker’s article.
In industrial chemistry we are comparing product concentrations like 99.5% or 99.9% etc. all the time. It’d be mighty non-intuitive to reverse to 1-X scales.
That graphical trick of shifting origins to make a difference seem more significant than it really is gets abused rampantly. I remember being annoyed by it in Catalogs like Sigma etc. At least from a utilitarian viewpoint learning to spot that graphical-abuse makes sense.
But the 1-X transform seems a red herring to this graph-abuse issue.
I think in this case we want to avoid the 1-X transform, because this just encourages another problem with making inferences from proportions: thinking that X times a small number is meaningful change. Using the numbers there — 1.1 and 5.4 — we would tend to focus on the fact that one bar is over twice as large as the other. But with smaller percentages we know this isn’t terribly useful, because both numbers are low. Imagine if one were .000021 and the other .000054. The bars would look the same!
To some extent, it depends what you want to show, but I think what we need here is comparison of both to a reference percentage, *not* 0. This could be the national average of smartphone ownership, for instance. This effectively becomes the “0” bar (but is labelled with its percentage on the axis). Something like this: NYT plot. I guess the point is that “0” is not always a good reference point.
eh, typo in the first para – .000021 should be .000011…
Depends what I’m most interested in, x or (1-x). For phone ownership my instinct is “Plot x.” In contrast, if I wanted to convey “Fraction of citizens who don’t have Ebola.” I’d show 1-x.
Exactly.
One cannot criticize the choice of X instead of 1-X based on closeness to 1 alone. It really is contextual based on what information matters / is to be conveyed.
Yeah, i agree with Lee up above. If 95 vs 98 (or whatever it is) is too close to 1, then it should also be that 5 vs 2 is too close to zero to matter. right?
The core issue is whether it is right to convey the message that phone ownership in the two states “indeed are very different”? Or is the correct message that the states are not very different in terms of phone ownership.
The 1-X transform reinforces the first message.
Rahul:
As I said in my post, it’s ridiculous to look at only 2 states when there are 50 of them. The variation among the 50 states would give some basis of comparison. Beyond this, it’s just foolish of Hacker to recommend the graph that makes the differences hard to visualize.
Isn’t the 2 vs 50 states point orthogonal to the 1 vs 1 – X issue?
Rahul:
If the numbers are graphed in a reasonable way, it doesn’t really matter if you plot x or 1-x. If the numbers are presentedas numbers, I prefer 1-x here because it’s easier to tell them apart. As I wrote in my Ramanjuan article, I consider tables (or presentation of numbers in text) as a crude form of graph. To compare 98.9% to 94.6% just takes more work than comparing 2.1% to 5.4%. If you really want to keep the numbers in the 90s, I’d recommend computing a national average (maybe it’s 96.1% or whatever) and then giving each state’s number as a + or – relative to that average. I really don’t think it’s a good idea to be throwing around numbers like 98.9% and 94.6%—that just seems like asking for trouble in interpretation.
Yes, that seems the right solution.
I think that Darrell Huff’s classic “How to Lie with Statistics” calls this a “Gee-Whiz Graph.”
Dave:
Darrell Huff was a hack.
Relating to the comment on multiple-choice tests, they should have no place in a statistics course. I created an online course in which the designers pushed for multiple-choice tests because we can then use the automatic scoring feature in the software. But in statistics, if there is a correct answer, it probably is something trivial (“compute the mean of these 10 numbers”). If the question is worth asking, the correct answer depends on certain assumptions. If there are assumptions, then the enterprising student will be arguing for points based on nuanced interpretation of the wording of the question or responses.
Kaiser:
I disagree. Sure, statistics is full of nuance, but it also involves specific skills. I’d like my students to be able to use the sqrt(p*(1-p)/n) formula (and to know when not to use it). And so on. Good multiple-choice questions can be difficult to write, though, I’ll admit that.
I don’t know how this represents anything, good or bad, since there are no intervals, scale, units or labels on this “graph”.
For once I’d like to see a y-axis labeled “height of y-axis “.