Uri Simonsohn just turned down the chance to publish a paper that could’ve been published in a top journal (a couple years ago I’d’ve said Psychological Science but recently they’ve somewhat cleaned up their act, so let’s say PPNAS which seems to be still going strong) followed by features in NPR, major newspapers, BoingBoing, and all the rest. Ted talk too, if he’d played his cards right, maybe even a top-selling book and an appearance in the next issue of Gladwell.
Wow—what restraint. I’m impressed. I thought Nosek et al.’s “50 shades of gray” was pretty cool but this one’s much better.
Here’s Simonsohn on “Odd numbers and the horoscope”:
I [Simonsohn] conducted exploratory analyses on the 2010 wave of the General Social Survey (GSS) until discovering an interesting correlation. If I were writing a paper about it, this is how I may motivate it:
Based on the behavioral priming literature in psychology, which shows that activating one mental construct increases the tendency of people to engage in mentally related behaviors, one may conjecture that activating “oddness,” may lead people to act in less traditional ways, e.g., seeking information from non-traditional sources. I used data from the GSS and examined if respondents who were randomly assigned an odd respondent ID (1,3,5…) were more likely to report reading horoscopes.
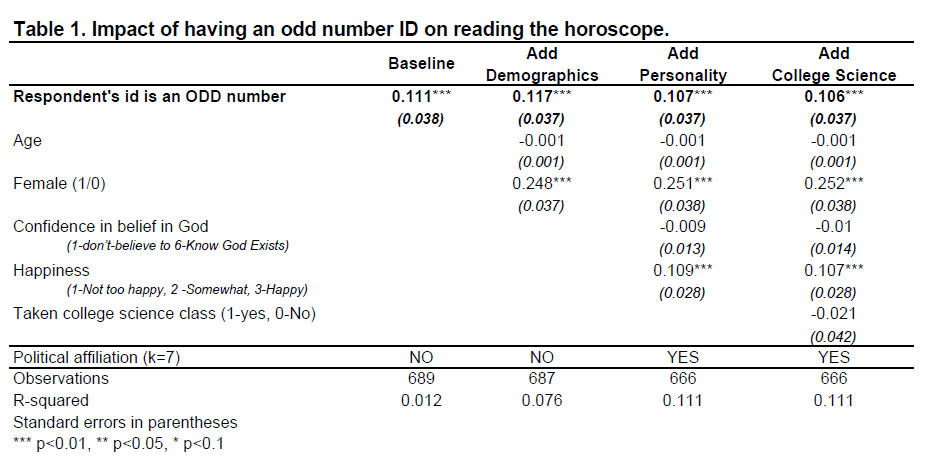
The first column in the table below shows this implausible hypothesis was supported by the data, p<.01:
People are about 11 percentage points more likely to read the horoscope when they are randomly assigned an odd number by the GSS. Moreover, this estimate barely changes across alternative specifications that include more and more covariates, despite the notable increase in R2.
But he blew the gaff by letting us all in on the secret.
Simonsohn describes the general framework:
One popular way to p-hack hypotheses involves subgroups. Upon realizing analyses of the entire sample do not produce a significant effect, we check whether analyses of various subsamples — women, or the young, or republicans, or extroverts — do. Another popular way is to get an interesting dataset first, and figure out what to test with it second.
Yup. And:
Robustness checks involve reporting alternative specifications that test the same hypothesis. Because the problem is with the hypothesis, the problem is not addressed with robustness checks.
Are you listening, economists?
A couple of concerns
But I do have a couple of concerns about Uri’s post.
1. Conceptual replications. Uri writes:
One big advantage is that with rich data sets we can often run conceptual replications on the same data.
To do a conceptual replication, we start from the theory behind the hypothesis, say “odd numbers prompt use of less traditional sources of information” and test new hypotheses.
Sure, but the garden of forking paths applies to replications as well. I know Uri knows this because . . . remember the dentist-named-Dennis paper? It had something like 10 different independent studies, each showing a statistically significant effect. Uri patiently debunked each of these, one at a time. Similarly, consider the embodied cognition literature.
Or, what about that paper about people with ages ending in 9? Again, it looked like a big mound of evidence, a bunch of different studies all in support of a common underlying theory—but, again, when you looked carefully at each individual analysis, there was no there there.
So, although I agree with Uri that there are some principles for understanding conceptual replications, I think he needs a big red flashing WARNING sign explaining why you can think you have a mass of confirming evidence, but you don’t.
2. Uri recommends looking at how the treatment effect varies in an predicted way:
A closely related alternative is also commonly used in experimental psychology: moderation. Does the effect get smaller/larger when the theory predicts it should?
This is fine but I have two problems here. First, “the theory” is often pretty vague, as we saw for example in the ovluation-and-voting literature. Most of these theories can predict just about anything and can give a story where effects increase, decrease, or stay the same.
Second, interactions can be hard to estimate: they have bigger standard errors than main effects. So if you go in looking for an interaction, you can be disappointed, and if you find an interaction, it’s likely to be way overestimated in magnitude (type M error) and maybe in the wrong direction (type S error).
This is not to say that interactions aren’t worth studying, and it’s not to say you shouldn’t do exploratory analysis of interactions—the most important things I’ve ever found from data have been interactions that I hadn’t been looking for!—but I’m wary of a suggestion to improve weak research by looking for this sort of confirmation.
Uri’s giving good advice if you’re studying something real, but if you’re doing junk science, I’m afraid he’s just giving people more of a chance to fool themselves (and newspaper editors, and NPR correspondents, and Gladwell, and the audience for Ted talks, and the editors of PPNAS, and so on).
3. Finally, this one I’ve discussed with Uri before: I don’t think the term “p-hacking” is broad enough. It certainly describes what Uri did here, which was to hack through the data looking for something statistically significant. But researchers can also do this without trying, just working through the data and finding things. That’s the garden of forking paths: p-values can be uninterpretable even if you only perform a single analysis on the data at hand. I won’t go through the whole argument again here; I just want to again register my opposition to the term “p-hacking” because I think it leads researchers to (incorrectly) think they’re off the hook if they have only performed a single analysis on the data they saw.
Summary
Uri writes:
Tools common in experimental psychology, conceptual replications and testing moderation, are viable solutions.
To which I reply: Only if you’re careful, and only if you’re studying something with a large and consistent effect. All the conceptual replications and testing of moderation aren’t gonna save you if you’re studying power pose, or ESP, or Bible Code, or ovulation and clothing, or whatever other flavor-of-the-month topic is hitting the tabloids.
“odd numbers prompt use of less traditional sources of information”
This isn’t a hypothesis. It is a either a (rather vague) prediction derived from some substantial hypothesis or a vagrant speculation. Think about it, where would an idea like that come from? From the presentation here, it seemes totally arbitrary and disconnected from everything else.
Simple syllogism: Being assigned an odd number makes you feel odd. Odd people read horoscopes. Therefore….
In essence, no more or less better founded than a lot of the priming literature: http://images.nymag.com/images/2/daily/2016/06/notrump_falk_gelman_icml.pdf
I was going to say check with Bem but who was it that did the retroactive prayer study?
Clearly assigning the odd numbers had a temporal-behavioural effect. Truly a Quantum result.
It’s intentionally ridiculous–but it takes a few minutes to sort out what it means.
I see Jonathan’s comment that it’s a syllogism–in which case it has bad premises and bad logic–but there’s something else going on here.
Did the respondents actually know their ID number? If not,then there’s no “priming” here whatsoever. If they did know their ID number, did this knowledge have any chance of influencing their horoscope reading habits? It seems unlikely, since their knowledge of their number would have directly preceded their responding to the question about horoscopes.
The only plausible (albeit silly) priming scenario would be as follows: Those with odd numbers (and who knew they were “odd” in this way) were more likely to REPORT reading horoscopes. There might have been many furtive horoscope readers among the even-numbered respondents.
Now, I question whether horoscope reading is “odd”; I have often felt “odd” for not doing it.
Here’s another hypothesis:
People with odd numbers feel subtly singled out as odd, so they’re more likely to try to give “mainstream” answers to peripheral questions, such as those about horoscope reading.
Diana said, “Did the respondents actually know their ID number? If not,then there’s no “priming” here whatsoever. If they did know their ID number, did this knowledge have any chance of influencing their horoscope reading habits? ”
This analysis misses some points.I’d break the first question up in finer detail:
Were the respondents told or shown their ID number? Did they look at it closely enough to notice that it was odd or even? Or can you make an argument (which seems far-fetched to me) that all (or even most) people unconsciously notice whether a number is even or odd?
I think you folks missed what was done, as I understand it. Respondents in the GSS were randomly assigned an odd number– “I used data from the GSS and examined if respondents who were randomly assigned an odd respondent ID (1,3,5…) were more likely to report reading horoscopes”–well after the survey was conducted. No one knew they were assigned an odd number because that was done by Simonsohn. It’s at best a spurious correlation.
In the actual GSS survey there are two questions about horoscope reading habits. I see no indication that Simonsohn followed up with the respondents.
The first question reads:
Now, for a new subject. Do you ever read your horoscope or a personal astrology report?
The second one reads:
Would you say that astrology is very scientific, sort of scientific, or not at all scientific?
I agree. That’s why I call it a spurious correlation. That’s his point. You can go into a large data set, set up something arbitrary, like coding people odd, based on a “hypothesis,” and correlate it with something, and find it significant.
I get that it’s a spurious correlation and that that was his point. I was just pointing out that the priming could not possibly have affected the respondents’ horoscope reading habits themselves, only their willingness to report such habits. And I meant this tongue in cheek.
And at worst the result of under-estimated standard errors? Or does he show that he fails to reject about 95% of all the subgroups he tests?
>> Robustness checks involve reporting alternative specifications that test the same hypothesis…
> Are you listening, economists?
Related reading – https://meansquarederrors.blogspot.de/2016/09/the-microfoundations-hoax.html
> … the most important things I’ve ever found from data have been interactions that I hadn’t been looking for!
The best guidance I ever got from a supervisor was to always ask “What does the data tell you?”
Andrew, I’m curious in your take on Roger Peng’s recent “A Simple Explanation for the Replication Crisis in Science” (http://simplystatistics.org/2016/08/24/replication-crisis/). Does that contribute understanding to this issue?
Bill:
Yes, I agree with Peng that the apparent rigor of randomization-based inferences has led people to be too credulous of claims derived from experiments and surveys. But I think statistical methods are part of the problem too. Peng refers dismissively to people who “blame for the entire crisis on p-values,” and of course I don’t blame the entire crisis on any single factor—but it does seem to me that p-values are part of the culture of overconfidence. I like Peng’s point that a crisis of replication happens, not just because published findings fail to replicate, but because this is a surprise to people (hence the “crisis”). Indeed, much of the crisis comes from researchers such as Kanazawa, Bem, Baumeister, Schnall, Cuddy, etc etc etc., who, when their findings are shown to have problems, just dig in rather than admitting they made a mistake. Again, though, I think misunderstanding of statistical methods is a big part of the problem. Most researchers really do seem to believe that if a comparison has “p less than .05” attached to it, that it has a high probability of replicating. And I think that we, the statistics profession, have to take a lot of the blame for this attitude.
I’ve been re-reading some of Deming’s work. He makes the claim that we don’t get knowledge from data; we get it from theory which is tested against and formed from data. From /The New Economics/ chapter 4: “Without theory, experience has no meaning. Without theory, one has no questions to ask. Hence without theory, there is no learning. Theory is a window into the world. Theory leads to prediction. Without prediction, experience and examples teach nothing.” Elsewhere he states the obvious, that theory is revised by people as they compare the predictions they make from theory to the real world results (data) they observe.
I hear in that similarities to a paper you once wrote about EDA including the comparison of models to data and to Peng’s statements in that posting.
Bill:
Yes. One challenge here, though, is that the power-pose researchers and the ESP researchers and the ovulation-and-clothing researchers and the embodied cognition researchers, all of them think they do have good theory backing their claims. A big part of their problem is statistical, in that they don’t recognize how weak their evidence is.
So how does one know that one has a good theory? From the above list, it seems that if the topic sounds crazy, it doesn’t really matter whether they think they have theory.
You might also find this helpful https://errorstatistics.files.wordpress.com/2015/12/gigerenzermarewski2015-121.pdf
And for your later comment on Deming, I couldn’t help but post these Bowie lyrics
Don’t believe in yourself
Don’t deceive with belief
The knowledge comes from death’s release [theory’s death?]
Thanks!
What I really want to know is whether the respondents who were assigned a prime number were more susceptible to priming – or eating prime rib on a regular basis. PNAS here I come….
“And I think that we, the statistics profession, have to take a lot of the blame for this attitude.” OK, but what to do about that. Professions that, by their nature, need to permit the greatest leeway for creative thinking and complex analysis are the slowest to adopt rigorous standards of professional behavior. Sure, we all recognize the need for ethical standards and place high value on acting in good faith at all times, but don’t we need principles that a board of experts develop using the Goldilocks rule – not too soft, not too hard, but just right, which varies by profession. Accountants in the U.S. are the most rules-based experts – since just after 1929. Actuaries perform more complex measurements and analysis than accountants. Actuarial Standards of Practice (ASOP) got started later than accountants, in 1985 and we are now up to 50 ASOPs with more on the way. In many situations, deviation from the standard is permitted, but require an explicit communication with the rationale.
As I understand your profession, there is widespread recognition of the many problems (garden of forking paths, etc.), but the proposed solution is primarily to identify and teach them. At some point, don’t you need to go beyond classroom instruction with detailed objective standards that can be used to call out methods and behavior that falls short? On a side note, its fascinating that the crisis of “false balance” in journalism –the failure of the existing ambiguous balance guideline – is coming to a head this week due to the extreme impact on presidential politics. Journalists have a too brief set of professional standards that are more about proscriptions than prescriptions. Please accept my apologies if there is already a movement underway to work on this, but I only find the ASA developments in March and June this year. I write about these types of issues on my blog and in particular here:
http://whentacticsbecomepolicy.blogspot.com/p/what-is-difference-between-actuary-and.html
Chris:
I’m skeptical of institutional solutions. Part of the reason I talk about taking the blame is that if you look at statistics textbooks, they typically are filled with success after success, which can give the impression that statistics is all about taking data, running the right analysis, finding statistical significance (or the Bayesian or machine-learning equivalent), and declaring victory. But the real world (outside the pages of PPNAS) isn’t always like that!
Chris said, “As I understand your profession, there is widespread recognition of the many problems (garden of forking paths, etc.), but the proposed solution is primarily to identify and teach them. ”
My impression is that the “recognition of the many problems (garden of forking paths, etc.)” is not widespread among many people who teach statistics. So there is a big need to educate the teachers, improve the textbooks, etc. This, however, can meet with resistance: the ideas that one needs to convey are not simple; teachers often oversimplify, not realizing that their intended improvements are actually distortions. This is partly what got us into the mess in the first place. So fixing the mess isn’t a simple matter.
Agree, that’s mostly what my link to Gigerenzer’s paper above is about.
OK, so fixing the problem is not a simple matter. I don’t mean to push a governing body (which raises a messy issue of enforcement) as much as comprehensiveness and completeness in organized documentation, and maybe a process for buy-in of practitioners. Right now I see the ASA Policy Statement, Ten Simple Rules, and your (Andrew’s) Handy Statistical Lexicon, among others. Seems this could all be brought together into a single organized set of documents and expanded with any gaps identified and filled. The methods being used to address the issue now feel a bit haphazard which makes convincing those who are resistant that much more difficult. In the actuarial profession, we started with the Interim Actuarial Standards Board in the mid-1980s, which sounded silly at the time – why the “Interim”? But that did help with resistance because it suggested openness to reasonable arguments against what they were proposing.
> not a simple matter.
I am not sure the Accounting Actuarial standards analogy works that well for many areas of Statistics.
Perhaps for analyzing randomized trails that were largely problem free but for stuff like non-randomized studies (most of whats done) things are really open ended. For instance http://sekhon.berkeley.edu/papers/opiates.orig.pdf “And the only designs I know of that can be mass produced with relative success rely on random assignment. Rigorous observational studies are important and needed. But I do not know how to mass produce them.”
Perhaps something more open ended and creative would be Advertising standards?
We have a paper in review in a mainstream psych journal that tries to illustrate the garden of forking paths problem that Andrew has written about so eloquently via a re-analysis of the data from a well-known psychology study. IF we are lucky enough to get it published somewhere it may help a little in educating mainstream researchers.
That sounds very interesting!
Should you not know already, and should you want to possibly use it, please note that you can upload pre-prints to https://osf.io/view/psyarxiv/
I saw Uri present an earlier version of this work and loved it, especially the demonstration that the effect doesn’t go away after controlling for other factors. There is a default intuition (that I am definitely vulnerable to) that it is a sign of robustness when a surprising finding stands strong even after some post hoc controls. But that’s one of Uri’s main points – by definition a spurious effect will remain standing in the face of reasonable alternative explanations.