Nate Cohn at the New York Times arranged a comparative study on a recent Florida pre-election poll. He sent the raw data to four groups (Charles Franklin; Patrick Ruffini; Margie Omero, Robert Green, Adam Rosenblatt; and Sam Corbett-Davies, David Rothschild, and me) and asked each of us to analyze the data how we’d like to estimate the margin of support for Hillary Clinton vs. Donald Trump in the state. And then he compared this to the New York Times pollster’s estimate.
Here’s what everyone estimated:
Franklin: Clinton +3 percentage points
Ruffini: Clinton +1
Omero, Green, Rosenblatt: Clinton +4
Us: Trump +1
NYT, Siena College: Clinton +1
We did Mister P, and the big reason our estimate was different from everyone else’s was that one of the variables we adjusted for was party registration, and this particular sample of 867 respondents had more registered Democrats than you’d expect, compared to Florida voters from 2012 with an adjustment for anticipated changes in the electorate for the upcoming election.
In previous efforts we’d adjusted on stated party identification but in this case the survey was conducted based on registered voter lists, so we knew party registration of the respondents. It was simpler to adjust for registration than stated party ID because we know the poststratification distribution for registration (based on the earlier election), whereas if we wanted to poststratify on party ID we’d need to take the extra step of estimating from that distribution.
Anyway, the exercise was fun and instructive. As Cohn put it:
We Gave Four Good Pollsters the Same Raw Data. They Had Four Different Results. . . . How so? Because pollsters make a series of decisions when designing their survey, from determining likely voters to adjusting their respondents to match the demographics of the electorate. These decisions are hard. They usually take place behind the scenes, and they can make a huge difference.
And he also provided some demographics on the different adjusted estimates:
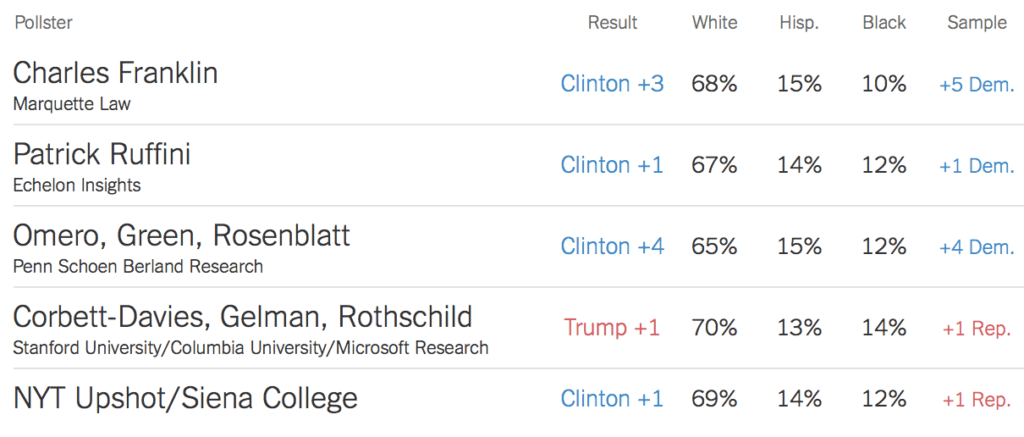
I like this. You can evaluate our estimates not just based on our headline numbers but also based on the distributions we matched to.
But the differences weren’t as large as they look
Just one thing. At first I was actually surprised the results varied by so much. 5 percentage points seems like a lot!
But, come to think of it, the variation wasn’t so much. The estimates had a range of 5 percentage points, but that corresponds to a sd of about 2 percentage points. And that’s the sd on the gap between Clinton and Trump, hence the sd for either candidate’s total is more like 1 percentage point. Put it that way, and it’s not so much variation at all.
So, we have a 5 point range, eliminating differences in question wording, or research procedures (robo or not, callbacks or not, etc.), and eliminating sampling error (same respondents).
The five point range is purely — well, we need a name for it, don’t we? What shall we call this? Statistician variance? Model choice variance? Adjustment variance?
I didn’t see, in the article, the naive estimate (i.e. just based on the raw, unweighted respondents).
Why not just “uncertainty”? Also, what’s the posterior 95% interval in Andrew’s estimate? What fraction of the range from others estimates does it cover?
All sources of variability are uncertainty; I was searching for a more specific name for this part.
I will note that these are four teams, working separately, with no axes to grind and no tenure view just ahead. If we had one lone researcher looking for an effect and running all four of these models — well, that would never happen, would it?
Andrew’s model could easily have a posterior high density interval that covers the whole range. Andrew, can you give a posterior density plot for your model?
That’s the part that bugs me: If it does have a high density that covers the whole range isn’t that like we are incentivizing models that hedge their predictions?
It really comes down to how much information do we have? It’s not so much about hedging predictions as honestly portraying the uncertainty we have. For example, if the high density region contains Trump +20 or Clinton +20 (Trump -20) then I’d say you’re inaccurately over-hedging. The polling data should tell us something more specific than that. But, if you’re being honest and you have some data, and you have legit uncertainty in the population’s composition and party identification, and the biases in non-response etc… and you come up with something like Trump -3 to +2 then you’re honestly saying really that it’s too close to call with any certainty.
Yes, but how do I distinguish between inherent uncertainty versus a crappy model that just gives a wide prediction?
@Rahul, you need to have the assumptions of the model explained to you, or see the code, or trust the author of the model on the basis of their prior history of making reasonable assumptions. From the prediction, you can’t. And, also, from a point prediction, you REALLY can’t.
In that sense isn’t it better to ignore the density & just look at the point estimate?
At least post hoc I can compare all these predictions to the result & see which pollster did better.
But if you invoke densities, as you did, it is very easy to get a model that’s always right.
@Daniel
I wonder if there could be a metric for model performance that considers the accuracy of prediction while simultaneously rewarding a narrower prediction density.
i.e. Given two models that were both right, isn’t the one that predicted a sharp density the better model?
Posterior entropy is pretty useful as a measure of tightness of the posterior distribution. after-the-fact you can use posterior density at the “correct” point to evaluate the earlier method, but this is only later, after you somehow find out what the correct value is, maybe by higher precision measurements or increased sample sizes etc.
How about “Pollster degree of freedom”?
In the total survey quality/error framework, this would be a component of processing error (i.e. weighting to the target population by adjusting the sampling weights, or constructing new weights a la MRP). Here “error” should be understood to include bias and variance. You sometimes see this broken out as “adjustment error” (in the first edition of the Groves et al book, for example).
I like “adjustment error”, although I’d prefer “adjustment variance”, to avoid the usual ambiguity around the meaning of “error”.
Thinking about this again, what I wrote may not be quite right. Generally a survey methodologist would think about adjustment variance as the variability of a (more or less) *fixed* adjustment procedure applied over repeated samples, with the bias of the procedure rounding out the overall adjustment error. That is, each of the different adjustment methods would have their own adjustment error (bias & variance) profile, where the bias and variance are again with respect to repeated sampling. Different choices for adjustment have different implications for adjustment error (variance), the same way that different choices of sampling designs and associated estimators have different implications for sampling error (variance).
Calling the variability *between* different adjustment methods “adjustment variance” muddies the waters in that regard, for the same reason that calling the variability between different sampling designs + estimators “sampling variance” would be confusing. We are (or I am at least) more used to naming the *within* component of variation (the sampling error of a particular sampling design, or the adjustment error associated with a particular adjustment procedure).
So yeah, some new terminology might be in order :)
In previous efforts we’d adjusted on stated party identification but in this case the survey was conducted based on registered voter lists, so we knew party registration of the respondents. It was simpler to adjust for registration than stated party ID because we know the poststratification distribution for registration (based on the earlier election), whereas if we wanted to poststratify on party ID we’d need to take the extra step of estimating from that distribution.
Stated party identification is different than registered party identification, so it seems like you are mixing and matching (if you are adjusting for stated party identification from previous elections). There’s been discussion before of whether party id is endogenous or not (I claim it could explain a good deal of the relatively minor variation that occurs in polling, while Andrew believes in the “disheartened nonresponse” hypothesis–see http://statmodeling.stat.columbia.edu/2016/08/05/dont-believe-the-bounce/ and comments under numeric–I do offer a way to test these two hypothesis). Be that as it may, using actual registration identification versus self-identification is more than enough to move a poll one to two percent–and recall, of course, that the difference between the highest and lowest estimate (with the n of 867) in this analysis is almost certainly not statistically significant (to use an argument Andrew has used in his published papers).
Numeric:
No, we’re using party registration in the survey and adjusting to party registration in the voting population, we’re not mixing and matching.
Can you post a posterior density plot for your model’s percentage point difference? I assume it’s not a delta function around Trump +1 ;-)
You’re not mixing and matching but I think that the cases where self reported party ID and registered party ID are different, even though it might be a small percent of the sample, might very well be meaningful. There are a lot of variables where self-reported and “objective” measures may meaningfully not align for various reasons. Gender and marital status are two that are obvious but there are lots of others where this well known.
Elin:
Yes, we could poststratify jointly on party registration and party ID, and this would give more information and should do better. We considered this option but decided against it, to avoid the effort that would be required in constructing a joint poststratification table on these two variables. It was easy to poststratify on party registration because that information is available from 2012 election records; party ID is tougher because we’d have to rely on surveys. I’m not actually sure how we got the poststratification table for party registration interacted with demographics.
I recall one part of your 2010 post on election forecasting, looking at Sam Wang and Nate Silver.
“Wang’s other mistake, I think, is his claim that “Pollsters sample voters with no average bias. Their errors are small enough that in large numbers, their accuracy approaches perfect sampling of real voting.” This is a bit simplistic, no? Nonresponse rates are huge and pollsters make all sorts of adjustments. In non-volatile settings such as a national general election, hey can do a pretty good job with all these adjustments, but it’s hardly a simple case of unbiased sampling.”
Clearly, surveys are not looking at unbiased sampling.
Nadia:
Yup. Wang’s been open about his methodology, and openness is good. Also sometimes you can do better by going inside the survey and not just looking at the topline.
Hi Andrew,
I have been following your blog for a while and really love it! Really thank you for doing it, can’t say how much I can thank you for taking the time to do it.
I have a peculiar question for you and I am asking the teacher here for an answer.
I would like to know more about statistics. As a matter of fact I would like to know as much as possible in statistics and I love reading. Therefore, for a student that let’s say have no knowledge in statistics that want to be an “expert” in statistics could you recommend a list of books that gradually can teach him statistics?
I’m not sure if this is a serious question, but I’m treating it as one. I have been in this poster’s position, and have a long answer to his question: take courses. See for example:
http://vasishth-statistics.blogspot.de/2015/02/getting-statistics-education-review-of.html
Yes, but courses are typically going to teach what you might call “standard” statistics, which starts with things like sampling error of the mean, and moves rapidly to t tests and chi-squared tests and other NHST based stuff.
I’ve heard really good things about McElreath’s Statistical Rethinking as the basis of a course that moves directly to Bayesian thinking : http://xcelab.net/rm/statistical-rethinking/
but I haven’t actually looked at the book myself, and I’m not sure what the background would be for this book/course.
I’ve read McElreath’s book, it is really good, and is a great basis for a Bayes only course. But I suspect the full import of his opening chapters will only be clear to those who have already been exposed to—and burned by—the frequentist paradigm in general and NHST in particular. The complete beginner will have no idea what he’s talking about. Maybe his lectures fill in the missing background.
Also, it is vital to understand the frequentist paradigm (and to paraphrase a student of mine, a simple test of whether you understand it is to check whether you are still using it). You need to be able to communicate with the broader audience, and therefore have to know the frequentist approach. When I go to a psycholinguistics conference, 99% of the presenters are using frequentist methods. The situation must be similar in psych. We can’t not teach this stuff.
Cohn really emphasizes that there is no sampling error. So certainly the point estimates are indeed different, but does the data support the conclusion that some pair of estimators don’t have the same limit?
That is, some of these methods might be more efficient than others, but are converging to the same thing. (I suspect that isn’t true for your method vs. the others, but perhaps the others are more similar.)
This could be tested using a seemingly unrelated estimators test (more or less a Durbin–Wu–Hausman test).
Dean:
As the saying goes, asymptotically we are all dead.
Yee gads — even in NZ we are getting predictions…http://www.nzherald.co.nz/world/news/article.cfm?c_id=2&objectid=11716182 … T/F to 13 questions though? ???
Is Fig 1 in the paper how you would generally recommend that proportion differences are visualised?
It seems the lines connecting the dots serves no purpose other than making it easier to see the difference between the dots. Bars would do that too.
Anon:
I think connecting the dots makes the patterns clearer and the differences easier to visualized. Sure, you could provide all the information bars—or, for that matter, in a table—but then it’s a lot harder for me to see the big picture.
No matter the particular model and all the adjustments, the central limit theorem and psephology can take one only so far in Florida. According to what I read, the 2012 race in Florida was so close that Nate Silver arbitrarily split its 29 electoral votes, giving 10 to Obama and 19 to Romney.
Although it was little noted, Silver was quite wrong on two of the 33 U.S. Senate races, the ones in Montana and North Dakota. His model gave the Republican candidates a 65.6% and 92.5% chance of winning, respectively. More than likely, his model suffered from the lack of polling done in those sparsely populated and sparsely polled states.
Andrew,
This sounds like a very big deal. Shouldn’t you be looking at all the polling results to see if there is a systematic bias?
Elsewhere, you talk about how unreliable Rasmussen is, and attribute it to their right-wing leanings. In this election, most public figures (Hollywood, prestige press, debate moderators, you-name-it) have come out openly against Trump. Is it possible that pollsters are indulging in a wee bit of thumb-on-the-scale here? Are they ignoring a systematic oversampling of Democrats? Why is the LA Times/USC poll so far from the others?
Terry:
Here’s my recent post on Rasmussen polls. I did not attribute their problems to right-wing leanings. I have no idea what are the leanings of Rasmussen. You are perhaps confusing me with some other writer.
Regarding your other point: I don’t know. The “thumb on the scale” metaphor isn’t quite right, though, in that there’s typically no reasonable unadjusted number. To continue with the metaphor of the scale, some adjustment is needed in any case. That’s a key challenge of modern polling.
My apologies. You did not attribute right-wing leanings to Rasmussen. It was the communication from Alan Abramowitz that suggested the link by lumping Fox’s poll with Rasmussen’s. But I could be wrong there too.
Anyway, there’s a curious poll out by NBC News/Wall Street journal today showing Hillary up by 14%. The curious thing is that it was done over only 2 days and polled only 447 people. None of their previous polls covered less than 4 days and often 5 days, and none of their other polls had less than 800 people and often 1000.
Why? Did they, perhaps unconsciously, stop the poll when they got agreeable results? Another degree of freedom in the garden of forking paths? Perhaps their rationale was that they stopped the poll the night of the second debate. But if so, why didn’t there start the poll two days earlier or two days later?
IIRC, somebody wrote a paper about this with regard to medical tests.
http://www.realclearpolitics.com/epolls/2016/president/us/general_election_trump_vs_clinton-5491.html#polls
Terry:
I don’t know about this particular poll, but I strongly doubt that they stopped because they liked the results. I expect they stopped because there’s a huge demand for news right now, so by stopping the poll they get faster news, more publicity, more clicks, a scoop, the usual aims goals in the news business.
We may be saying roughly the same thing, just in different ways.
The NBC/WSJ pollsters have, in the past, conducted 4 or 5 day polls and released the results after the entire poll was finished. The current poll is also a 4 or 5 day poll (they added another day of results today indicating the poll is ongoing). But this time, after only 2 days, Hillary was up 14% and they decided to release preliminary results. The RCP summary of polls shows no other instance of their doing this (see link below). Further, they released these results without mentioning the deviation from their usual procedure. The poll makes a big splash and is widely covered – so a big success for the pollsters.
Why did they do it? I think we basically agree. It was a dramatic result that would attract clicks. The 2-day results were so stunning that they didn’t want to wait for the full results which might be less dramatic (the file drawer bias). I go a step further and suggest that NBC/WSJ also likes these results, and I suspect they would not have released early results if the numbers had gone the other way.
To be fair, there is another, very good and honest reason to report the 2-day results: to distinguish between the pre-debate and post-debate periods. Such an honest pollster would report the pre-debate and post-debate results separately and compare the two. This would be very useful … basically an event study.
So now we have a third day of results. What did the pollsters actually do? They reported only the combined 3-day results (see NBC link below) and they headlined that Hillary’s lead is still gigantic.
But what were the results of the third day of polling? RCP shows Hillary’s lead dropped from 14% in the 2-day results to 10% in the 3-day results (RCP reports the head to head matchup). So the third day of polling showed Hillary in the lead by about 2%: (14% + 14% +2%) / 3 = 10%. (4-way results imply a Hillary lead of 5% on the third day.)
So, an honest pollster would have reported “Hillary’s lead skyrockets to 14% after lewd-tape release, but plummets to 2% after debate.
FWIW, I find your work extremely worthwhile and I intend no disrespect.
http://www.realclearpolitics.com/epolls/2016/president/us/general_election_trump_vs_clinton-5491.html
http://www.nbcnews.com/politics/first-read/poll-after-trump-tape-revelation-clinton-s-lead-double-digits-n663691