Anthony Fowler and Andy Hall write:
We reassess Achen and Bartels’ (2002, 2016) prominent claim that shark attacks influence presidential elections, and we find that the evidence is, at best, inconclusive. First, we assemble data on every fatal shark attack in U.S. history and county-level returns from every presidential election between 1872 and 2012, and we find little systematic evidence that shark attacks hurt incumbent presidents or their party. Second, we show that Achen and Bartels’ finding of fatal shark attacks hurting Woodrow Wilson’s vote share in the beach counties of New Jersey in 1916 becomes substantively smaller and statistically weaker under alternative specifications. Third, we find that their town-level result for beach townships in Ocean County significantly shrinks when we correct errors associated with changes in town borders and does not hold for the other beach counties in New Jersey. Lastly, implementing placebo tests in state-elections where there were no shark attacks, we demonstrate that Achen and Bartels’ result was likely to arise even if shark attacks do not influence elections. Overall, there is little compelling evidence that shark attacks influence presidential elections, and any such effect—if one exists—appears to be substantively negligible.
The starting point here is a paper presented by political scientists Chris Achen and Larry Bartels in 2002, “Blind Retrospection – Electoral Responses to Drought, Flu and Shark Attacks.” here’s a 2012 version in which the authors trace “the electoral impact of a clearly random event—a dramatic series of shark attacks in New Jersey in 1916” and claim to “show that voters in the affected communities significantly punished the incumbent president, Woodrow Wilson, at the polls,” a finding that has been widely discussed in political science over the past several years and was featured in Achen and Bartels’s recent book, Democracy for Realists.
Fowler and Hall make a convincing case that Achen and Bartels’s analysis was statistically flawed, that the statistically significance obtained in that observational analysis is misleading. The problems were correlation (making p-values not follow their nominal distribution) and forking paths (making it that much easier for the original researchers to find a statistically significant pattern and fit a story around it).
See more at the sister blog—for some reason, they don’t like cross-posting so I’ll send you there for the full story. Also, as discussed at the end of that post, I think Achen and Bartels have some good points in their book; their larger arguments do not rely on the validity of that shark-attack study.
Graphs can mislead and graphs can inform
There’s one thing I did want to talk about here which did not come up in that other post, and that’s the role of statistical graphics. Here’s the graph from Achen and Bartels showing the dramatic effect of shark attacks in the New Jersey 2016 election:
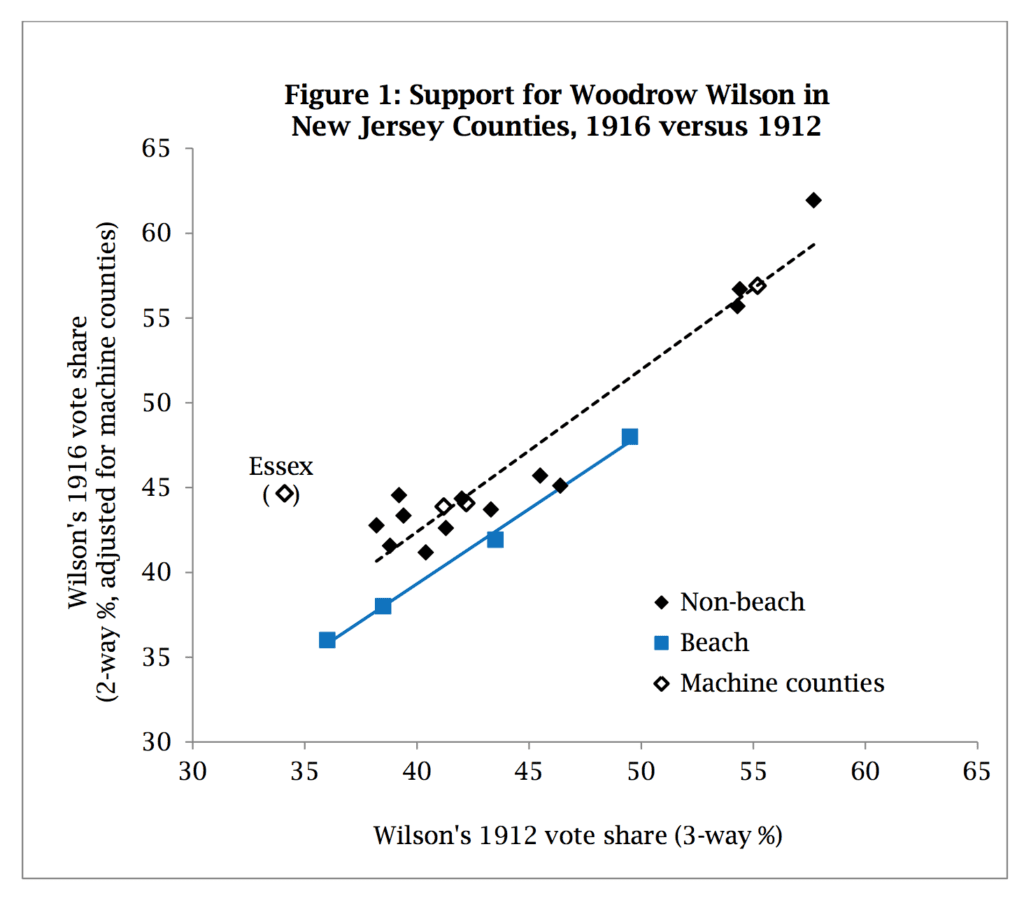
It looks pretty impressive. Actually, though, as Fowler and Hall discuss, it’s not such a stunning pattern:
1. Election results are correlated, so those 4 beach counties are not really 4 independent data points.
2. This graph is not actually displaying the raw data! Check out the y-axis label: “adjusted for machine counties.” If you look at this scatterplot Fowler and Hall made of the raw data, those 4 beach counties don’t stand out at all:
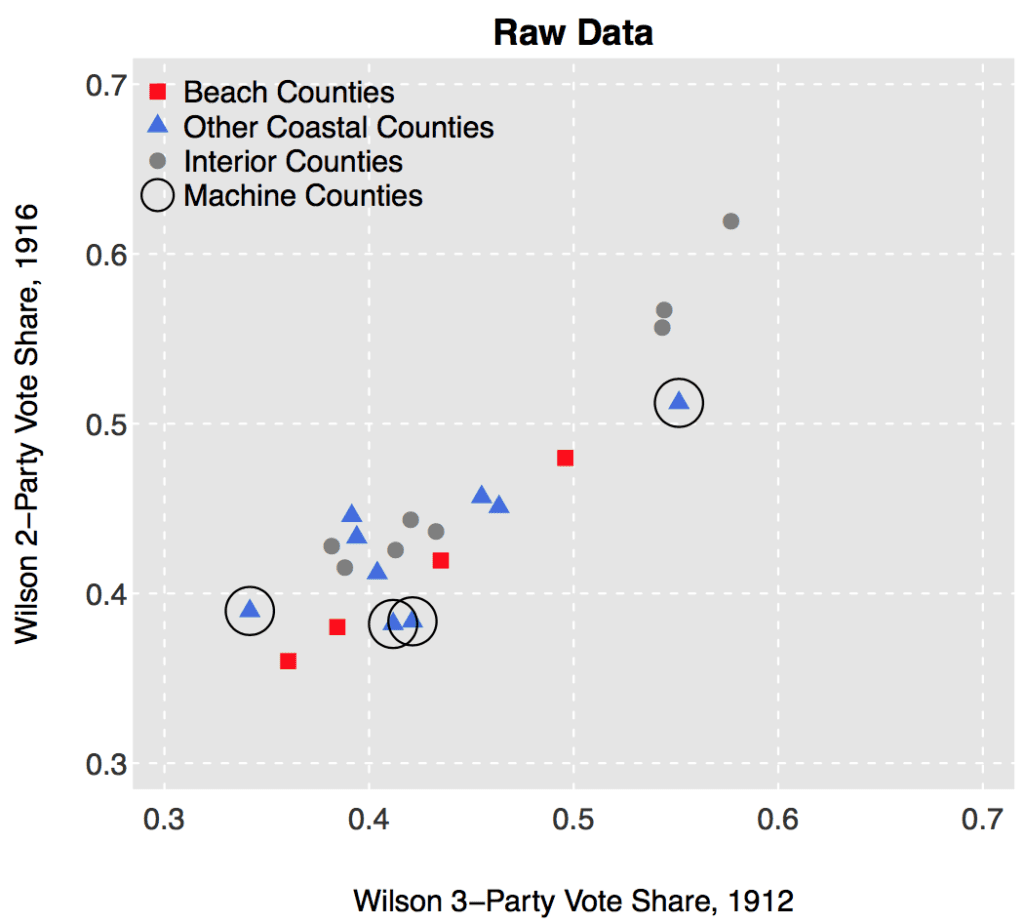
This is not to say that one shouldn’t plot adjusted data—I do it all the time, it’s a useful statistical technique—but the point is that the adjustment matters, and that’s where forking paths come in. There are many different adjustments one might make.
So, yes, that graph looks pretty convincing but it’s hiding some serious statistical problems, which is why Fowler and Hall convincingly argue that it’s all too easy to find statistical significance in this setting, even in the absence of any underlying effect.
Hall adds:
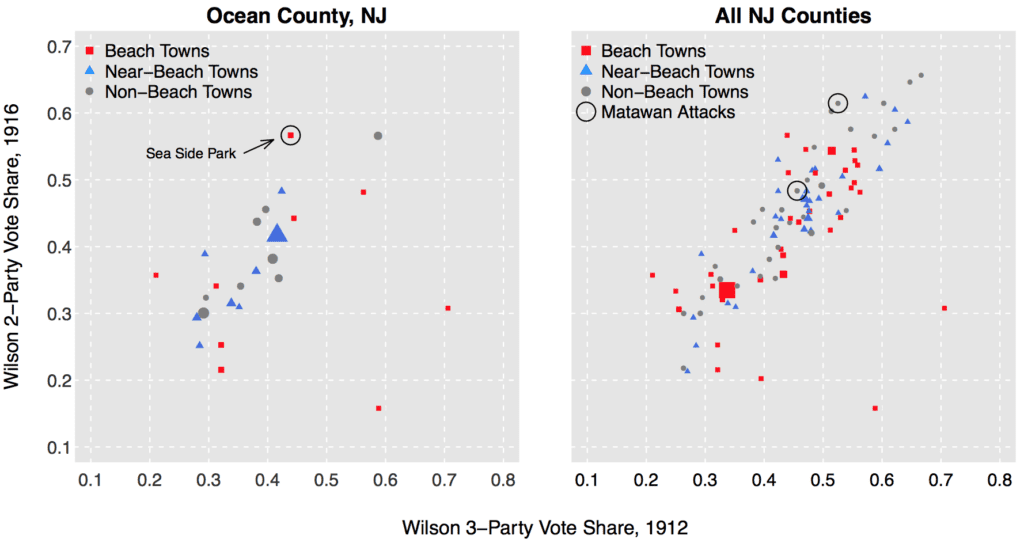
The graph of towns shows some interesting stuff as well. In the left panel, we highlight Sea Side Park, the “treated” town that was accidentally omitted from their analysis, and which had a positive swing for Wilson after the attacks. In the right panel, we show how the analysis changes once you (a) bring in the towns in the other beach counties and (b) include the two Matawans (borough and township, respectively), where two of the four attacks occurred (up river from the beach, which is why A+B choose to omit them)—these two towns also saw positive swings towards Wilson in 1916.
P.S. Best comment comes from Raghu, who writes:
When I started reading, I assumed that “shark attack” was some sort of metaphor for something political — a vicious ad, maybe. But no, it’s really shark attacks!
Indeed. Shark attacks, himmicanes, power pose, the contagion of obesity . . . it’s been a wacky decade or so in social science. Let’s hope we’re getting over it.
P.P.S. I just happened to notice this uncritical review of Achen and Bartels book. No mention of shark attacks, though!
I might be ignorant here, but what’s “Machine Counties”?
“Machine county” referred to counties whose politics were heavily controlled by Democratic rivals to Wilson. The authors considered them to be outliers from the rest of the state and threw them out of the analysis. I think Andrew is arguing here that you can always convince yourself to throw out data that disagrees with your results enough to create a result… it’s okay to throw out some data but you have to be disciplined and reasonable about it.
I agree that results which are robust to different types of adjustment are more convincing than results which only show up under a single adjustment, but when methods of adjustment disagree, isn’t it possible that one approach is correct and the others are not? And if this is possible, isn’t it possible that the authors have a defense for their choice of adjustment over the others? I don’t know enough about the details of this particular analysis, but while showing that the raw data do not display the pattern of interest reduces my confidence in their result, it is not obvious to me that the raw data is the “right” way to look at it. If the absence of the pattern in the raw data was not addressed in the original paper, it seems only fair to take a wait and see attitude towards their results pending response.
Reminds me of Asimov’s Foundation: if I could identify the random event that will affect the next election because that’s what the pattern on the wall says it will be this time. One part of Foundation was the way it drew lines between past and present and future events and discerned a pattern that could be read.
How many random events correlate to a result? If the event being measured is something big, like a Presidential election, I’d suppose the answer is immense. You know, for example, the incidence of excessive flatulence in upstate NY, as indicated by doctor’s/hospital visits for gastrointestinal distress, directly reflects a reduction in the vote for Dewey in 1948. And if the event is small, then the correlations must be equally immense because I’m often hungry when others are hungry, which is kind of amazing and thank heaven restaurants figured this out and open for lunch! I think the willingness of people to attribute meaning to numbers that link to other numbers is nearly bottomless.
A guiding principle of research should be “everything is correlated with everything else”. The exact opposite is assumed by the current NHST paradigm.
Once more, a link to one of my favorite websites: http://tylervigen.com/spurious-correlations
I like that one, too! I use it in Stats class to drive home the point that correlation =/= causation. The students get a big kick out of it!
When I started reading, I assumed that “shark attack” was some sort of metaphor for something political — a vicious ad, maybe. But no, it’s really shark attacks! Jonathan’s quote above, “I think the willingness of people to attribute meaning to numbers that link to other numbers is nearly bottomless,” is excellent. All of this stuff is really no better, and no different, than astrology.
So under some specifications it holds, and others it doesn’t. How do we decide between these?
Ehrich:
I don’t think it holds at all. Fowler and Hall show that Achen and Bartels’s procedures will be able to get statistical significance from just about any data. So their p-value provides essentially zero evidence for their claim. It’s kangaroo time all over again.
In relation to the issue of random, we have a nice example of a near opposite form right now. I’m thinking about the FBI decision to bring up the existence of Wiener related emails in the last days of October before the election. If I were the FBI director, trying to see it from his perspective, he’s in a no win situation: if he doesn’t then he’s pilloried for the next several years by the GOP trying to blame him for the Hillary win and if he does then he is viewed as a partisan tool trying to influence the election. I think he may have fallen back on process: there is an investigation and so I’m going to say this, at first blush, appears to fit the investigation. That is, it’s an October surprise but maybe it’s just one of those which pop up as part of life instead of something intentional. But I also think the FBI action might have been different if the election were actually closer because then the announcement that they found emails without having any reason to suspect they say anything important beyond what’s already known might really turn history. That raises an interesting question about how one’s actions are valued in context: in the context of a large Hillary lead, this action seems likely to have no actual effect but in the context of a closer election it might be crucial. Say the FBI says this in a really close race and the result changes and then the FBI says the emails were nothing: you can’t undo the vote, can’t replay it with no announcement. Or in general, the effect in terms of vote totals could be large in number but have no effect on the result or the vote changes might be less numerically and yet have a complete effect, a binary shift of no to yes and yes to no, all based on the pre-existing condition of the state of the race within overlapping contexts, meaning the context of the election ends on the vote date but the answer about the emails may occur beyond that date (or within it, though that case is less interesting in this formulation). So in shark attack ideas, the effect of random correlations would tend to be small or they’re less likely to be random, so a correlation of a shark attack sequence to vote totals may or may not be there but it’s silly to think it has any power of effect. It’s essentially a homeopathy example: the relation if any is so small that it’s roughly equivalent to a solution diluted and diluted and diluted until any effect it might have is random or ascribed through anecdote.
I heard an hour or so ago on the radio that there is an additional complication in the FBI/emails/etc release: As a result of the Bill Clinton/Loretta Lynch tarmac meeting in June, there was a call for Lynch to recuse herself from the investigation into the Hillary Clinton emails, which she did, turning the investigation over to the FBI. However, an NPR interviewee today (I think it was Robert Gonzalez, but I can’t find a link to his interview — which is labeled “will be posted later today”) said that the normal protocol in such a situation would be to turn the investigation over to the deputy secretary of state, rather than to the FBI.
(Lynch did criticize the FBI for going public at this time: http://www.usatoday.com/story/news/nation/2016/10/29/ag-lynch-objected-fbi-director-going-public-email-review/92949970/)
I think all of this is proof that we have to be humble about what we don’t know and *can’t* know. Shark attacks may (or may not) play an important role in US elections, but so do a lot of other minor factors as well, and the resulting effects are likely so small and minor that it’s undetectable. It might not even be possible to study these attacks’ effects, nor would it be a good use of time or money. There are inherent limits to our knowledge…we can’t know everything, and we have to be comfortable with uncertainty.
Andrew, in our previous discussion about “omnicausal effects” (http://statmodeling.stat.columbia.edu/2016/03/03/more-on-replication-crisis/#comment-264954) you said “I also think there’s a theorem in there somewhere, about how large the consistent effects can be without creating an impossible system that spins out of control”. Has there been any work on writing out that theorem? This theorem could be useful to try to prevent the “wacky decade” from being replicated again. After all, most hypothesis seems reasonable with enough news coverage and backing of experts, and we can’t just rely on our own intuitions (after all, I too believe in the shark attack hypothesis). If we could study a effect’s consistent effects and determine if they are likely to be true or not, that should be able to reduce potential fears about believing in something silly for a period of time.
Realist:
No theorem yet, but I’ve talked with Ben Goodrich and others about it, and we’ve even run some simulations. So I still have hope on this one.
The “wacky decade” has been valuable. If techniques that many used to accept as standard have led to absurd results, we now have to double check the more plausible results. The data might not be supporting our priors as much as we’d like to think they do.
+1 — but provided we do indeed double check the more plausible results.
There must be some key concept I’m not getting about the “Figure 1” plot. So, there’s one regression line for beach counties and another regression line for non-beach counties. The regression lines seem to differ in offset, but their slopes seem the same.
I would think that shark attacks in 1916 hurting Wilson’s vote-share would be demonstrated by the beach county regression line having a lesser slope than the non-beach county regression line.
The difference in regression line offset just means that Wilson started out less popular in beach counties and continued to be less popular in beach counties (compared to non-beach counties).
So, how does the Figure 1 plot show a “dramatic effect of shark attacks”? As far as I can tell, it shows no effect at all.
Is this the same Christopher Achen who has written a few statistics books?