David Leonhardt of the NYT asked a bunch of different people, including me, which of various Romney-won states in 2012 would be likely to be won by a Democrat in 2020, 2024, or 2028, and which of various Obama-won states would go for a Republican in any of those future years.
If I’m going to do this at all, I’ll do it by fitting a model. And this seemed like a good opportunity for me to learn to fit some time series in R.
I decided to fit a Gaussian process model (following the lead of Aki in the birthday problem) with separate time series for each state and each region, with the country partitioned into 10 regions that I set up to roughly cluster the states based on past voting trends. For the national level time trend I just assumed independent draws from a common distribution because the results jump around a lot from year to year. And I fit to data from 1976, just cos Yair happened to send me a state-by-state electoral dataset from 1976, but also because 1972 and before looked different enough that it didn’t really seem to make so much sense to include those early years in the analysis.
For Gaussian processes it can be tricky to estimate length-scale parameters without including some regularization. In this case I played around with a few options and ended up modeling each state and each region as the sum of two Gaussian processes, which meant I needed short and long length scales. After some fitting, I ended up just hard-coding these at 8 and 3, that is, 32 years and 12 years. The long scale is there to allow low-frequency trends which will stop the model from automatically regressing to the mean when extrapolated into the future; the short scale fits the curves you can see in the data.
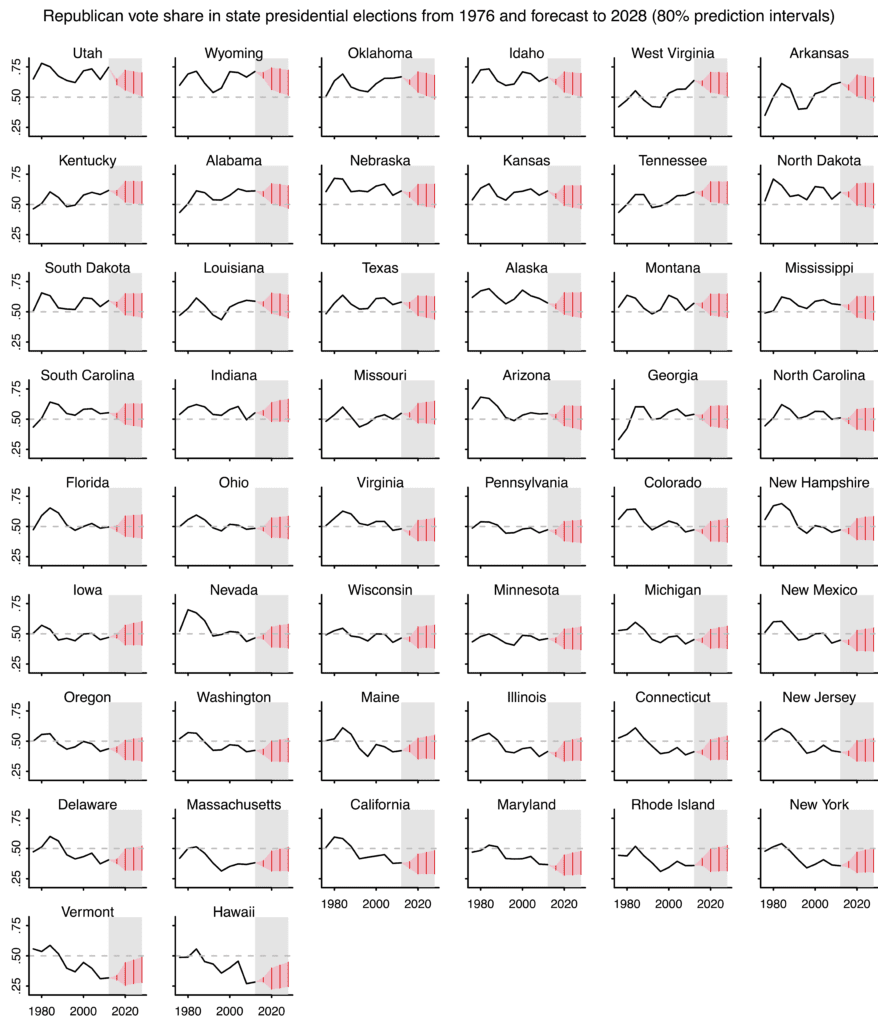
I’ll first graph for you the data (1976-2012) and future 80% predictive intervals. The intervals for 2016 come from Pierre-Antoine Kremp’s open-source Stan-based forecast from last week; the intervals for 2020-2028 come from simulations of our fitted model in the generated quantities block of our Stan program.
I have a bit more to say about the model. But, first, here are the results:
The forecast intervals are wide because just about anything could happen with national swings. Recall that our data includes the 1984 Reagan landslide, on one extreme, and some solid victories for Bill Clinton and Barack Obama on the other. That’s all fine—a forecast has its uncertainty, after all—but it makes it hard to see much from these forecasts.
So I made a new set of graphs showing each state relative to the national average popular vote. To calculate the popular vote for future elections I simply plugged in the state-by-state two-party vote from 2012, which isn’t perfect but will do the job for this purpose. And here’s what we got:
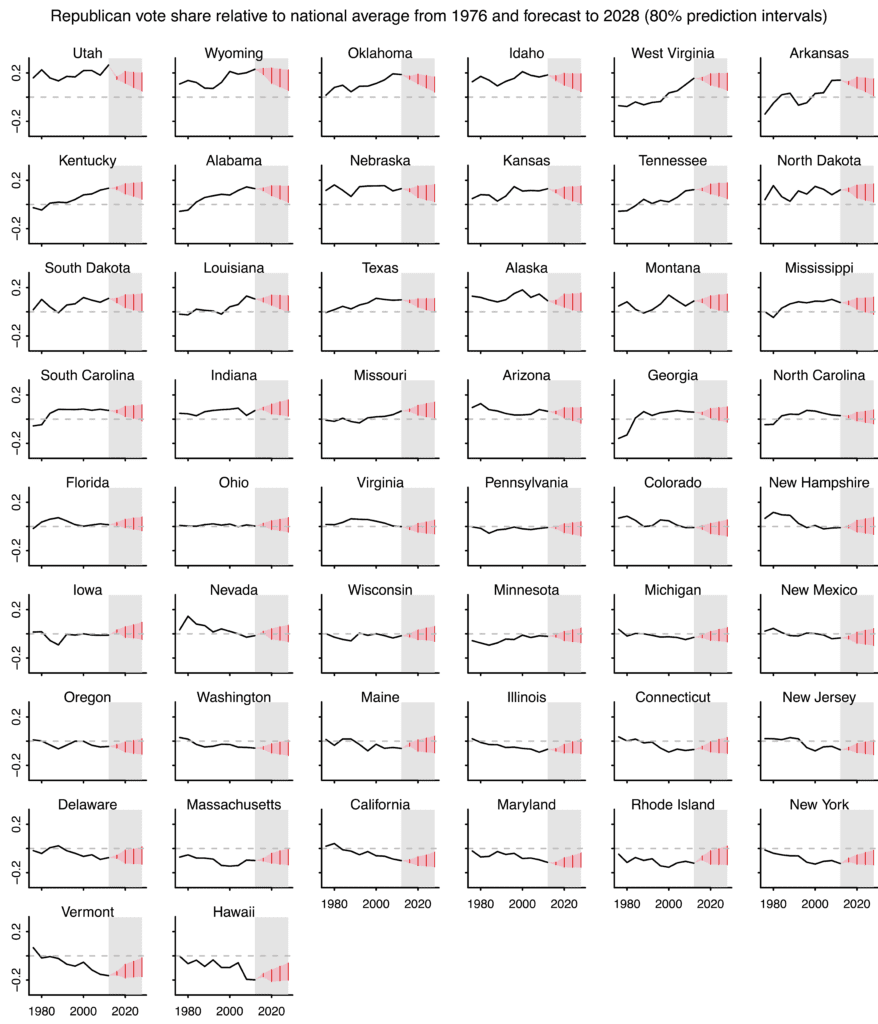
The model is complicated in a statistical sense in that it has state, regional, and national levels; but it’s “dumb” in that it uses nothing more than past vote totals and a forecast of the 2016 vote; this model does not account for demographic trends. So, for example, our model does not “know” that New Mexico has so many Latinos; it just sees that New Mexico has gradually been trending Democratic in recent decades. And our model does not “know” to associate Mitt Romney’s religion with the Republican spike in Utah in 2012. And so on. So in that sense we see this model as a baseline, a sort of blank slate or minimal starting point upon which further information can be added.
So these graphs aren’t the answer, they’re a first step. In any case, I found the exercise to be a helpful first step in training my intuition on Gaussian process time series models. And we can use the simulation to predict all sorts of things. For example, we have Iowa with a 23% chance of being won by the Democrats in 2020/2024/2028, a 20% chance of being won by the Republicans in all three elections, and a 57% chance of it being split. You can easily estimate this sort of probability using posterior simulations.
Here’s the Stan program, state_forecasts.stan:
data {
int T; # number of years
int J; # number of states
int K; # number of regions
matrix[J,T-1] y; # Republican vote share by state, 1976 through 2012
int region[J]; # Region indexes
int T_new; # number of future years
int T_all; # T + T_new
real scale_GP_region_long;
real scale_GP_state_long;
real scale_GP_region_short;
real scale_GP_state_short;
/* int home_state_dem[T];
int home_state_rep[T];
real beta_home_state; */
matrix[J,T] two_party_turnout;
vector[J] forecast_2016;
matrix[J,J] cov_2016;
}
transformed data {
real times[T_all];
matrix[J,T] relative_turnout;
for (t in 1:T_all){
times[t] = t;
}
for (t in 1:T){
relative_turnout[,t] = two_party_turnout[,t]/exp(mean(log(two_party_turnout[,t])));
}
}
parameters {
matrix[K,T] GP_region;
matrix[J,T] GP_state;
vector[T] delta;
vector[J] gamma;
vector[K] mu;
real mu_delta;
real sigma_delta;
real sigma_mu;
vector[K] sigma_gamma;
real sigma_gamma_0;
real sigma_error_region;
real sigma_error_state_1;
real sigma_error_state_2;
real sigma_GP_region_long;
real sigma_GP_state_long;
real sigma_GP_region_short;
real sigma_GP_state_short;
# real alpha;
vector[J] rvote_2016;
}
transformed parameters {
matrix[T_all,T_all] cov_GP_region;
matrix[T_all,T_all] cov_GP_state;
matrix[J,T] turnout_weight;
cov_GP_region = cov_exp_quad(times, sigma_GP_region_long, scale_GP_region_long) + cov_exp_quad(times, sigma_GP_region_short, scale_GP_region_short);
cov_GP_state = cov_exp_quad(times, sigma_GP_state_long, scale_GP_state_long) + cov_exp_quad(times, sigma_GP_state_short, scale_GP_state_short);
for (t in 1:T_all){
cov_GP_region[t,t] = cov_GP_region[t,t] + sigma_error_region^2;
cov_GP_state[t,t] = cov_GP_state[t,t] + sigma_error_state_1^2;
}
for (t in 1:T){
for (j in 1:J){
turnout_weight[j,t] = relative_turnout[j,t]^(-.5);
}
}
}
model {
matrix[J,T] y_pred;
matrix[T_all,T_all] L_GP_region;
matrix[T_all,T_all] L_GP_state;
matrix[J,T] y_full;
y_full[,1:(T-1)] = y;
y_full[,T] = rvote_2016;
rvote_2016 ~ multi_normal(forecast_2016, cov_2016);
L_GP_region = cholesky_decompose(cov_GP_region);
L_GP_state = cholesky_decompose(cov_GP_state);
for (k in 1:K) {
GP_region[k,] ~ multi_normal_cholesky(rep_vector(0, T), L_GP_region[1:T,1:T]);}
for (j in 1:J) {
GP_state[j,] ~ multi_normal_cholesky(rep_vector(0, T), L_GP_state[1:T,1:T]);}
delta ~ normal(mu_delta, sigma_delta);
gamma ~ normal(mu[region], sigma_gamma[region]);
for (t in 1:T){
for (j in 1:J){
y_pred[j,t] = delta[t] + gamma[j] + GP_region[region[j],t] + GP_state[j,t];
}
}
to_vector(y_full) ~ normal(to_vector(y_pred), sigma_error_state_2*to_vector(turnout_weight));
mu ~ normal(0, sigma_mu);
mu_delta ~ normal(.5, .5);
sigma_mu ~ normal(0, 1);
sigma_delta ~ normal(0, 1);
sigma_gamma ~ lognormal(log(sigma_gamma_0), log(2));
sigma_gamma_0 ~ normal(0, 1);
sigma_GP_region_long ~ normal(0, 1);
sigma_GP_state_long ~ normal(0, 1);
sigma_GP_region_short ~ normal(0, 1);
sigma_GP_state_short ~ normal(0, 1);
sigma_error_region ~ normal(0, 1);
sigma_error_state_1 ~ normal(0, 1);
sigma_error_state_2 ~ normal(0, 1);
}
generated quantities {
matrix[J,T_new] y_new;
matrix[J,T_new] y_new_pred;
vector[T_new] delta_new;
matrix[K,T_new] GP_region_new;
matrix[J,T_new] GP_state_new;
for (t in 1:T_new){
delta_new[t] = normal_rng(.5, sigma_delta); // Center at 50%, not at mu_delta
}
# GP code:
{
matrix[K,T_new] mu_region_new;
matrix[J,T_new] mu_state_new;
matrix[T_new,T] K_transpose_div_Sigma_region;
matrix[T_new,T] K_transpose_div_Sigma_state;
matrix[T_new,T_new] Tau_region_new;
matrix[T_new,T_new] Tau_state_new;
matrix[T_new,T_new] L_GP_region_new;
matrix[T_new,T_new] L_GP_state_new;
K_transpose_div_Sigma_region = cov_GP_region[(T+1):T_all, 1:T] / cov_GP_region[1:T, 1:T];
K_transpose_div_Sigma_state = cov_GP_state[(T+1):T_all, 1:T] / cov_GP_state[1:T, 1:T];
mu_region_new = GP_region * K_transpose_div_Sigma_region';
mu_state_new = GP_state * K_transpose_div_Sigma_state';
Tau_region_new = cov_GP_region[(T+1):T_all, (T+1):T_all] - K_transpose_div_Sigma_region * cov_GP_region[1:T, (T+1):T_all];
Tau_state_new = cov_GP_state[(T+1):T_all, (T+1):T_all] - K_transpose_div_Sigma_state * cov_GP_state[1:T, (T+1):T_all];
L_GP_region_new = cholesky_decompose(Tau_region_new);
L_GP_state_new = cholesky_decompose(Tau_state_new);
for (k in 1:K){
vector[T_new] sim;
sim = multi_normal_cholesky_rng(mu_region_new[k,]', L_GP_region_new);
GP_region_new[k,] = sim';
}
for (j in 1:J){
vector[T_new] sim;
sim = multi_normal_cholesky_rng(mu_state_new[j,]', L_GP_state_new);
GP_state_new[j,] = sim';
}
}
for (j in 1:J){
for (t in 1:T_new){
y_new_pred[j,t] = delta_new[t] + gamma[j] + GP_region_new[region[j],t] + GP_state_new[j,t];
y_new[j,t] = normal_rng(y_new_pred[j,t], sigma_error_state_2*turnout_weight[j,T]);
}
}
}
The model isn’t bad. It looks like a lot at first but I know what each piece is doing. One goal we have for the Stan language development is to have ways of coding this sort of model more compactly. But for now it’s ok; we can work with it.
And here’s the R script:
setwd("~/AndrewFiles/research/2012")
library("arm")
library("rstan")
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
past_pres <- read.table("state-election-results-1976-thru-2012.txt", header=TRUE)
forecast_2016_data <- read.table("forecast_2016.txt", header=TRUE)
cov_2016_data <- read.table("cov_2016.txt", header=TRUE)
T <- 11
T_new <- 3
J <- 50
K <- 10
state_groups <- list(c("ME","NH","VT","MA","RI","CT"),
c("NY","NJ","PA","MD","DE"),
c("OH","MI","IL","WI","MN"),
c("WA","OR","CA","HI"),
c("AZ","CO","NM","NV"),
c("IA","NE","KS","ND","SD"),
c("KY","TN","MO","WV","IN"),
c("VA","OK","FL","TX","NC"),
c("AL","MS","LA","GA","SC","AR"),
c("MT","ID","WY","UT","AK"))
region_names <- c("New England", "Mid-Atlantic", "Midwest", "West Coast", "Southwest","Plains", "Border South", "Outer South", "Deep South", "Mountain West")
region <- rep(NA, J)
for (k in 1:length(state_groups)){
ok <- state.abb %in% state_groups[[k]]
region[(1:J)[ok]] <- k
}
home_state <- read.table("home_state.txt", header=TRUE)
year <- 1972 + 4*(1:(T+T_new))
two_party_turnout <- array(NA, c(J,T))
y <- array(NA, c(J,T-1))
national_mean <- rep(NA, T)
home_state_dem <- rep(NA, T)
home_state_rep <- rep(NA, T)
forecast_2016 <- rep(NA, J)
cov_2016 <- array(NA, c(J,J))
for (j in 1:J){
for (t in 1:(T-1)){
state_ok <- as.character(past_pres$state) == state.abb[j]
year_ok <- past_pres$year == year[t]
ok <- state_ok & year_ok
if (sum(ok)!=1) stop(cat(c(j,t)))
two_party_turnout[j,t] <- past_pres$dem[ok] + past_pres$rep[ok]
y[j,t] <- past_pres$rep[ok]/two_party_turnout[j,t]
}
two_party_turnout[j,T] <- two_party_turnout[j,T-1]
ok <- as.character(forecast_2016_data$state) == state.abb[j]
if (sum(ok)!=1) stop(cat(c(j,t)))
forecast_2016[j] <- forecast_2016_data$rvote[ok]
}
for (j1 in 1:J){
ok1 <- as.character(cov_2016_data$state) == state.abb[j1]
for (j2 in 1:J){
ok2 <- colnames(cov_2016_data) == state.abb[j2]
cov_2016[j1,j2] <- cov_2016_data[ok1,ok2]
}
}
for (t in 1:T){
home_state_dem[t] <- (1:J)[state.abb==as.character(home_state$D_state)[t]]
home_state_rep[t] <- (1:J)[state.abb==as.character(home_state$R_state)[t]]
}
y_relative <- array(NA, dim(y))
relative_turnout <- array(NA, c(J,T-1))
for (t in 1:(T-1)){
national_mean[t] <- sum(y[,t]*two_party_turnout[,t]) / sum(two_party_turnout[,t])
y_relative[,t] <- y[,t] - national_mean[t]
relative_turnout[,t] <- two_party_turnout[,t]/exp(mean(log(two_party_turnout[,t])));
}
state_ok <- as.character(past_pres$state) == "DC"
year_ok <- past_pres$year == 2012
ok <- state_ok & year_ok
dc_turnout_2012 <- past_pres$dem[ok] + past_pres$rep[ok]
## Fit the Stan model
T_all <- T + T_new
scale_GP_region_long <- 8
scale_GP_state_long <- 8
scale_GP_region_short <- 3
scale_GP_state_short <- 3
fit <- stan("state_forecasts.stan", init=function(){list(rvote_2016=forecast_2016)})
print(fit, pars=c("rvote_2016", "sigma_GP_region_long", "sigma_GP_state_long", "sigma_GP_region_short", "sigma_GP_state_short", "sigma_error_region", "sigma_error_state_1", "sigma_error_state_2", "mu_delta", "sigma_delta", "sigma_gamma", "sigma_gamma_0", "mu", "sigma_mu"))
## beta_home_state_hat <- mean(extract(fit)$beta_home_state)
beta_home_state_hat <- 0
home_state_adj <- array(0, c(J, T-1))
for (t in 1:(T-1)){
home_state_adj[home_state_dem[t], t] <- home_state_adj[home_state_dem[t], t] - beta_home_state_hat
home_state_adj[home_state_rep[t], t] <- home_state_adj[home_state_rep[t], t] + beta_home_state_hat
}
y_relative_adj <- y_relative - home_state_adj
## Compute quantiles of forecasts
rvote_2016_sims <- extract(fit)$rvote_2016
y_new_sims <- extract(fit)$y_new
n_sims <- dim(y_new_sims)[1]
sims <- array(NA, c(n_sims, J, T_new+1))
sims[,,1] <- rvote_2016_sims
sims[,,2:(T_new+1)] <- y_new_sims
relative_sims <- array(NA, dim(sims))
national_mean_future <- array(NA, c(n_sims, T_new+1))
for (s in 1:n_sims){
for (t in 1:(T_new+1)){
national_mean_future[s,t] <- (sum(sims[s,,t]*two_party_turnout[,T]) + .1*dc_turnout_2012) / (sum(two_party_turnout[,T]) + .1*dc_turnout_2012)
relative_sims[s,,t] <- sims[s,,t] - national_mean_future[s,t]
}
}
quants <- c(.1, .25, .5, .75, .9)
quants_sims <- array(NA, c(J, T_new+1, length(quants)))
quants_relative_sims <- array(NA, c(J, T_new+1, length(quants)))
for (j in 1:J){
for (t in 1:(T_new+1)){
quants_sims[j,t,] <- quantile(sims[,j,t], quants)
quants_relative_sims[j,t,] <- quantile(relative_sims[,j,t], quants)
}
}
## Put data together
past_data <- y
dimnames(past_data) <- list(state.name, seq(1976,2012,4))
past_data_relative <- y_relative
dimnames(past_data_relative) <- list(state.name, seq(1976,2012,4))
future_bounds <- array(NA, c(J, 12), dimnames=list(state.name, paste(rep(seq(2016,2028,4), c(rep(3,4))), c("10th","50th","90th"), sep="_")))
future_bounds_relative <- array(NA, c(J, 12), dimnames=list(state.name, paste(rep(seq(2016,2028,4), c(rep(3,4))), c("10th","50th","90th"), sep="_")))
for (t in 1:(T_new+1)){
future_bounds[,3*(t-1) + (1:3)] <- quants_sims[,t,c(1,3,5)]
future_bounds_relative[,3*(t-1) + (1:3)] <- quants_relative_sims[,t,c(1,3,5)]
}
write.table(round(past_data, 3), "past_data.txt")
write.table(round(past_data_relative, 3), "past_data_relative_to_national_vote.txt")
write.table(round(future_bounds, 3), "future_bounds.txt")
write.table(round(future_bounds_relative, 3), "future_bounds_relative_to_national_vote.txt")
## Graph data and predictions
pdf("state_forecasts_1.pdf", height=7, width=6)
par(mfrow=c(9,6), oma=c(0,0,3,0), mar=c(1.5,1.5,0,0), mgp=c(.5,.25,0), tck=-.03)
ordering <- order(y[,T-1])
for (jj in 1:50){
j <- rev(ordering)[jj]
plot(0, 0, xlim=c(1,T_all), ylim=c(.2, .8), bty="l", xlab="", xaxt="n", ylab="", yaxt="n", type="n")
polygon(rep(c(T-1, T_all), c(2,2)), c(-1,1,1,-1)*.32 + .5, col="gray90", border=NA)
polygon(c(rev((T-1):T_all), (T-1):T_all), c(rev(quants_sims[j,,1]), rep(y[j,T-1], 2), quants_sims[j,,5]), col="pink", border=NA)
lines(1:(T-1), y[j,1:(T-1)], lwd=1)
for (t in T:T_all){
lines(rep(t,2), quants_sims[j,t-T+1,c(1,5)], lwd=.5, col="red")
}
abline(.5, 0, col="gray", lty=2)
years <- seq(1980, 2020, 20)
axis(1, (years-1972)/4, rep("", length(years)))
if (jj>44){
axis(1, (years-1972)/4, years, cex.axis=.7)
}
axis (2, c(.25, .50, .75), rep("", 3))
if (jj%%6 == 1){
axis(2, c(.25,.50,.75), c(".25",".50",".75"), cex.axis=.7)
}
mtext(state.name[j], side=3, line=-.2, cex=.6)
}
mtext("Republican vote share in state presidential elections from 1976 and forecast to 2028 (80% prediction intervals)", side=3, line=1.7, cex=.7, outer=TRUE)
dev.off()
pdf("state_forecasts_2.pdf", height=7, width=6)
par(mfrow=c(9,6), oma=c(0,0,3,0), mar=c(1.5,1.5,0,0), mgp=c(.5,.25,0), tck=-.03)
ordering <- order(y[,T-1])
for (jj in 1:50){
j <- rev(ordering)[jj]
plot(0, 0, xlim=c(1,T_all), ylim=c(-.3, .3), bty="l", xlab="", xaxt="n", ylab="", yaxt="n", type="n")
polygon(rep(c(T-1, T_all), c(2,2)), c(-1,1,1,-1)*.32, col="gray90", border=NA)
polygon(c(rev((T-1):T_all), (T-1):T_all), c(rev(quants_relative_sims[j,,1]), rep(y_relative[j,T-1], 2), quants_relative_sims[j,,5]), col="pink", border=NA)
lines(1:(T-1), y_relative[j,1:(T-1)], lwd=1)
for (t in T:T_all){
lines(rep(t,2), quants_relative_sims[j,t-T+1,c(1,5)], lwd=.5, col="red")
}
abline(0, 0, col="gray", lty=2)
years <- seq(1980, 2020, 20)
axis(1, (years-1972)/4, rep("", length(years)))
if (jj>44){
axis(1, (years-1972)/4, years, cex.axis=.7)
}
axis (2, c(-.2, 0, .2), rep("", 3))
if (jj%%6 == 1){
axis(2, c(-.2,.2), cex.axis=.7)
}
mtext(state.name[j], side=3, line=-.2, cex=.6)
}
mtext("Republican vote share relative to national average from 1976 and forecast to 2028 (80% prediction intervals)", side=3, line=1.7, cex=.7, outer=TRUE)
dev.off()
## For each state, give prob dist for #R in next 3 elections
predict_r_win <- array(NA, c(J, T_new + 1), dimnames=list(state.name, 0:T_new))
y_new_r_win <- ifelse(extract(fit)$y_new > .5, 1, 0)
for (j in 1:J){
r_win_total <- array(NA, c(n_sims,J))
for (s in 1:n_sims){
r_win_total[s,j] <- sum(y_new_r_win[s,j,])
}
for (i in 1:(T_new+1)){
predict_r_win[j,i] <- mean(r_win_total[,j]==(i-1))
}
}
pfround(predict_r_win[rev(ordering),], 2)
write.table(round(predict_r_win, 2), "predict_r_win.txt")
GP_state_sim <- extract(fit)$GP_state
GP_state_new_sim <- extract(fit)$GP_state_new
pdf("state_forecasts_3.pdf", height=7, width=6)
par(mfrow=c(9,6), oma=c(0,0,3,0), mar=c(1.5,1.5,0,0), mgp=c(.5,.25,0), tck=-.03)
ordering <- order(y[,T-1])
for (jj in 1:50){
j <- rev(ordering)[jj]
plot(0, 0, xlim=c(1,T_all), ylim=c(-.15, .15), bty="l", xlab="", xaxt="n", ylab="", yaxt="n", type="n")
polygon(rep(c(T-1, T_all), c(2,2)), c(-1,1,1,-1)*.32, col="gray90", border=NA)
for (s in 1:50){
lines(1:(T-1), GP_state_sim[s,j,1:(T-1)], lwd=.1)
lines((T-1):T_all, c(GP_state_sim[s,j,(T-1):T], GP_state_new_sim[s,j,1:T_new]), lwd=.1, col="red")
}
abline(0, 0, col="gray", lty=2)
years <- seq(1980, 2020, 20)
axis(1, (years-1972)/4, rep("", length(years)))
if (jj>44){
axis(1, (years-1972)/4, years, cex.axis=.7)
}
axis (2, c(-.1, 0, 1), rep("", 3))
if (jj%%6 == 1){
axis(2, c(-.1,.1), cex.axis=.7)
}
mtext(state.name[j], side=3, line=-.2, cex=.6)
}
mtext("Estimated smooth curves for each state (50 posterior draws)", side=3, line=1.7, cex=.7, outer=TRUE)
dev.off()
Yeah, yeah, I know the R code is ugly. It also includes some data such as candidates’ home states that I didn’t end up including in the final model. (I can explain more on this if you’d like.)
Also the whole setup is a mess, dumping all this code in the blog post like this. Better would be for me to put this in a Stan notebook or docker or github or whatever but I don’t really know how to do this. Or even just add some sort of appendix to Kremp’s markdown file.
We in the Stan team have a plan for a Stan model repository where users like me will be able to upload models and data and scripts in a more user-friendly, reproducible way.
For now, I put all the data and code for our model in this zipfile.
Nothing against notebooks or docker or …, but take a look, too, at Emacs’ orgmode and org-babel.
I hadn’t seen cov_exp_quad() in the wild before. Very exciting! Will save a lot of effort.
Jim:
Aki Vehtari, Dan Simpson, and Rob Trangucci helped me set up the model.
This is excellent — I love the analysis posts. I am working on a problem where I need to smooth noisy estimates from the ACS, and this blog post makes a lot of the steps clearer. Thanks!
A possible extension could include investigating the extent to which macroeconomic variables impact election results.
It seems that it would be good to use only part of the data to develop the model parameters, then test it against, say, 2012-2016. Although with the uncertainty ranges, maybe you couldn’t tell anything anyway.
Tom:
I was thinking of doing that, but then I didn’t bother for the reason that you say. But it’s still worth doing for someone who has the time. The code’s all there!
The other thing that you could do is run the model backward, that is exclude early years and see how well they are predicted. Gaussian time series models are symmetrical so they predict backward or forward in time identically.
I’m not sure what you mean by “users like me”, but we already have a GitHub repository for example models and a way of viewing them online as case studies.
The bottleneck, I suspect, for most users will be (a) learning knitr or Jupyter, (b) learning how to make a pull request on GitHub, and (c) being organized enough with scripting and data setup to make things reproducible.
What do you need to make this easier for you?
Bob:
We talked about this at the Stan meeting but it might have been after you left. What will work for me is a walk-through form which tells me where to put the Stan program, the R code, the data, and so on.
You were writing this during the PSA session?
Olav:
No, of course not! During the PSA session I was either speaking or taking notes on what I was going to speak on. I wrote this last night and scheduled it to appear in the morning.
From the 2000 through 2012 elections, the Republican-Democratic split by state correlates highly with the rate of younger (age 18-44) white women being married according to a Census Bureau report in 2002. For example, the average white woman in Utah was married 17 years between 18 and 44, while the average white woman in Massachusetts has been married 12 years (and the average white woman in the District of Columbia 7 years).
The Marriage Gap has generally been more powerful than the famous Gender Gap.
I first figured this out in December 2004 looking at the 2000 and 2004 elections. The effect was a little less strong in 2008, but it bounced back remarkably in 2012. (I expect it to decline from 2012 to 2016 due to the differences between Romney and Trump.)
You could probably use this to make forecasts. Unfortunately, I haven’t seen any new sources since 2002 allowing the Years Married stat to be calculated.
Your first paragraph seems confusing as written. IS the following what you mean?
“… correlates highly with the length of marriage for younger (age 18 – 44) married women…. For example, the average length of marriage for white women aged 18 – 44 in Utah was 17 years, while the average length of marriage for white women aged 18 – 44 in Massachusetts was 12 years (and 7 years for such women in the District of Columbia).”
This seems like a nearly impossible exercise in the first place, given how much could happen in 4, 8 or 12 years, no?
I’m interested by modeling exercise. Particularly I am wondering if you feel the exercise yielded much information? That is, to my eye, the model appears to have predicted stability around whatever the prior vote share was and where the historical data are more extreme (Utah, Wyoming, Vermont, Hawaii for example) you get what looks like regression to the national mean. Would alternate methods of modeling the problem arrived at vastly different results (say, simply taking a weighted average)?
Adam:
You get what you put in. We didn’t put in much so we didn’t get much. What worked with this exercise was that we were able to compute things like the probability that a given state would go Republican in three state elections, which is what Leonhardt had asked me. I wouldn’t really have a good way of computing such a thing without using a probability model.
I missed a section of your comments where you made clear it was a first step (not accounting for changing demographics, etc.) and at first I thought to write that you can just ignore my comment, but I guess it now raises the question for me about how do you figure out which things the model ought to include to become better?
Adam:
You ask, “how do you figure out which things the model ought to include to become better?” My answer is that you need to bring in prior information, either in the most direct sense by thinking about what are the important issues that are not in the model (in this case, demographics are an obvious thing to look at), or indirectly by looking at the state-level predictions and seeing if any of them seem wrong. “Seems wrong” = in contradiction to some prior belief.