I was impressed by Pierre-Antoine Kremp’s open-source poll aggregator and election forecaster (all in R and Stan with an automatic data feed!) so I wrote to Kremp:
I was thinking it could be fun to compute probability of decisive vote by state, as in this paper. This can be done with some not difficult but not trivial manipulations of your simulations. Attached is some code from several years ago. I’ll have to remember exactly what all the steps were but I don’t think it will be hard to figure this all out. Are you interested in doing this? It would be fun, and we could get it out there right away.
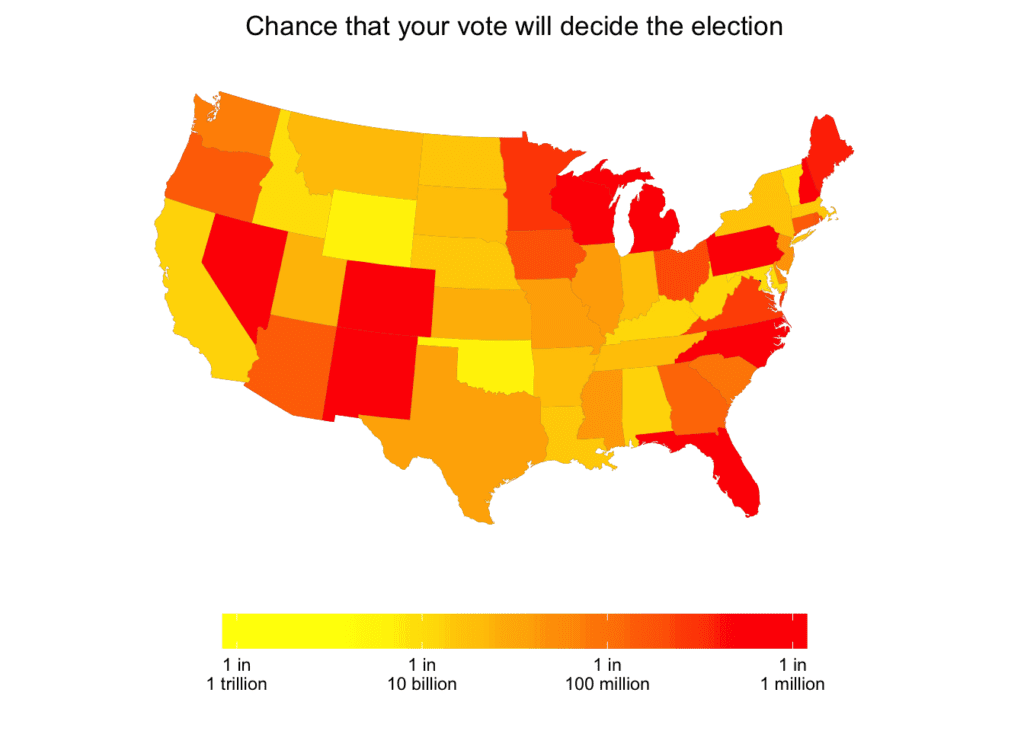
And he did it! We went back and forth a bit on the graphs and he ended up with this map:
Best places to be a voter, in terms of Pr(decisive) are New Hampshire and Colorado (in either state the probability that your vote determines the election is 1 in a million); Nevada, Wisconsin, or Pennsylvania (1 in 2 million), Michigan, New Mexico, North Carolina, or Florida (1 in 3 million), or Maine (1 in 5 million). At the bottom of the list are a bunch of states like Maryland, Vermont, Idaho, Wyoming, and Oklahoma where you can forget about your vote making any difference in the electoral college.
(That said, I’d recommend voting for president even in those non-swing states because your vote can still determine who will win in the popular vote, or it might be enough to cause a change in the rounded popular vote, for example changing the outcome from 50-50 (to the nearest percentage point) to 51-49. Or enough to make the vote margin in 2016 exceed Obama’s margin over Romney in 2012. Any of these can affect perceptions of legitimacy and mandates, which could be a big deal in the election’s aftermath.)
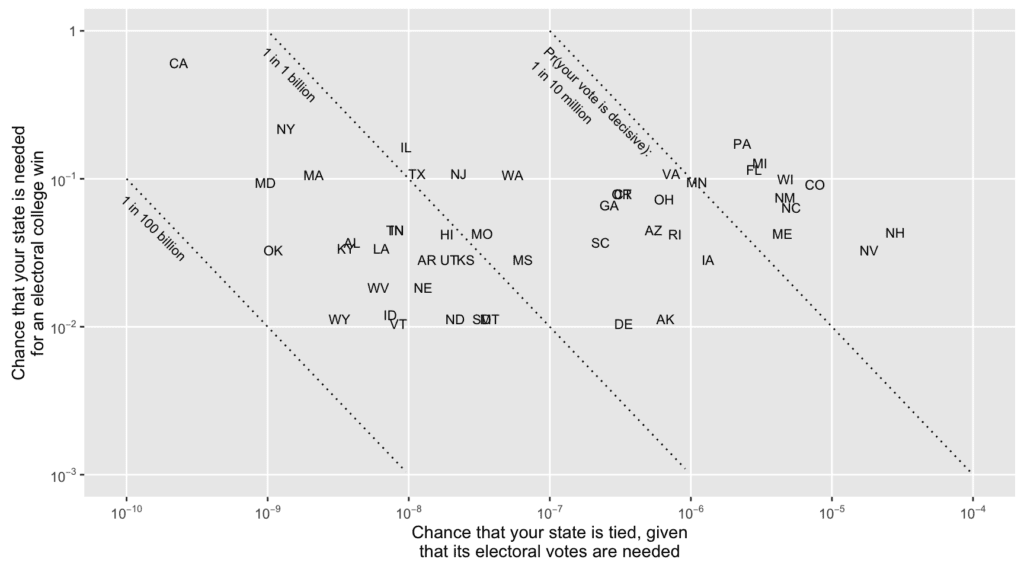
We also made a graph similar to the one from our paper from the 2008 election, decomposing the probability of decisive vote as:
Pr (your vote is decisive) = Pr (your state’s electoral votes are necessary for the winning candidate) * Pr (the vote in your state is tied | your state’s electoral votes are necessary)
We ignore the thing with Maine and Nebraska possibly splitting their electoral votes, and we assign DC’s 3 votes to the Democrats.
Here’s the graph showing Pr (your state’s electoral votes are necessary) vs. Pr (the vote in your state is tied | your state’s electoral votes are necessary):
The diagonals are iso-lines for constant Pr(decisive), so you see the swing states on the upper right of the graph and the less close states on the left, in the 1-in-a-billion range and below.
Despite these probabilities being low, I do think it can be rational to vote, for the reasons discussed in this paper (or more briefly here, or even more briefly in my article scheduled to appear today in Slate); see also my comment here for clarification of some common points of confusion on this issue.
P.S. By the way, and speaking of reproducible research, I’m really glad that I had the code that I used to those calculations back in 2008, and also that I’d written it up as a paper. It would’ve been a bit of work to reconstruct the calculations with only the code or only the written description. But with both available, it was a piece of cake.
“I’d recommend voting for president … because your vote can still determine who will win in the popular vote, or it might be enough to cause a change in the rounded popular vote…”
Sorry, that can not be true. The odds of a single vote accomplishing that are zero in the real world. None of your discussion contradicts that directly.
Also, your “charity” rationale for personal voting presumes a generally collectivist political ideology toward society and government. There are other ideologies among many Americans.
What is your estimate of the overall margin of error in actually counting/recording all the popular votes cast for President across America?
IMO it is easily 1-2% and likely higher. The abstract ideal of democratic voting differs much from its practical reality on Election Day. Voting, counting votes, and officially reporting votes is a very complex process in national elections… with many sources of possible error & opportunities for malicious interference.
Gibson:
1. The probability that your vote will determine the popular vote winner is on the order of 1 in 10 million. 1 in 10 million is not zero. All of us live in the real world. And in the real world, a 1 in 10 million chance is not trivial, if it’s multiplied by a large enough gain.
2. It is well known that voters vote for what they think is the best for the country. This has nothing to do with a collectivist ideology. For example, suppose you voted for Ronald Reagan in 1980, not because you thought he’d give you a personal tax cut, but because you thought that his anti-collectivist economic policies would be good for the U.S. economy and world peace and freedom. You’d be voting for what you thought was good for the country and the world. Nothing collectivist about that!
3. Regarding margins of error, recounts, etc.: I discuss this in the Slate article which they unfortunately don’t seem to have posted yet. This question comes up a lot and it turns out it’s not an issue at all. See the appendix on the last page of this article for a full explanation.
If it comes down to anywhere near 1 vote deciding things, we can be sure that various other factors will actually be the deciding factor, see Gore vs Bush. Whether it’s the supreme court, some local election official who decides against or for a recount in his district, or some “volunteers” who make sure that a few extra hanging chads get thrown out on one side vs another… all the way up to a coordinated terrorist firebombing attacks on some critical ballot counting station. also there’s the very real issue of non-transparent electronic voting machine bugs or security exploits. None of these are in your model. Fortunately 1 in 10 million chance that we have to deal with those things is low. People are willing to say things like “pshaw a terrorist firebombing of a ballot counting station? that’ll never happen…” but it seems probably 2 or 3 orders of magnitude more likely than that a single vote will decide the presidential election.
Daniel:
Nonononononono. Your 1 vote can be the one that triggers the recount or the lawsuit or whatever. See the appendix on the last page of this article for a full explanation.
Sure, but it’s still the case that a terrorist attack or some concerted hacking attempt on polling computers is far more likely to be the deciding factor by a couple orders of magnitude.
And that these kinds of situations are not included in your model. In the presence of even say 2000 people in the whole world who are willing to aggressively cheat the US vote and who could potentially each affect state vote by say 5000 votes without being detected, what is the probability of your vote being decisive?
In case it’s not clear, these two effects, your one vote, and the cheaters, are not independent, you can’t just say “well there’s the cheating, and then you’ve got some new vote state, and then your one vote can be deciding for that new vote state at 1/10M” because the effect of cheaters is to actively push the vote state away from the even split, thereby reducing the chance of being close to an even split in the first place.
For illustration purposes, suppose we have a simple majority vote issue (not electoral votes). There are 100 million people voting on it exactly. Based on polling etc, our predictive distribution for the vote fraction is something like normal(0.5,.01) (that is things are within 1 percentage point). Now, we want to include the effect of active cheating pushing things away from the even split. we take our normal distribution and multiply it by a function that provides a barrier to the really close split, within 5000 votes is 5000/100,000,000 which is +- .00005
so we have a new predictive distribution taking into account the cheating effect
normal_pdf(0.5,.01) * (1-.999*exp(-1/2*((x-.5)/0.00005)^2)) * Z where Z is a number very close to 1 that renormalizes everything. Now it looks like a normal curve with a very tight notch taken out of it at the center.
That is, the density of outcomes very near the even split under pure voting is reduced by 3 orders of magnitude under realistic conditions because of the active “push” away from even split by cheaters.
Is this a terrible model for how things work? It’s hard to know. Cheating exists for sure, we hear about it every year. The question is, does it actually act to push the vote away from even split, or does it mostly cancel out just causing even more entropy and hence a little wider uncertainty in the outcome than the 1%? How strong is the effect? I don’t know, but I do know that if you don’t model it at all, and you start to throw out numbers like 1/10M or 1/100M of decisive vote, you’re estimating something that is so unlikely that the effect of ignoring the small amount of cheating might well swamp the estimate.
Daniel:
Suppose there’s a 1-in-1000 chance of one of those things happening (hacking, etc). Then Pr(your vote is decisive) becomes, say, 0.999e-6 instead of 1e-6. Even if you allow for dependence, sure, maybe it becomes 0.9e-6. Not much of a big deal.
Let’s put it another way. Suppose a voter’s chance of dying this year is 1/80 (based on a rough calculation that avg lifespan is approx 80). So the chance of dying tomorrow is (1/365)*(1/80) = 3e-5, which is quite a bit higher than the probability of your vote being decisive. Fine, you might die tomorrow. But you might not, and in that case your vote can make a difference.
In other words, we don’t even have 1 significant figure in the estimate of the base 10 logarithm of the probability of decisiveness tomorrow thanks to the very real possibility of choking on a hotdog at lunch today.
Daniel:
No. Pr(your vote is decisive | you don’t die tomorrow) is 1e-6 (if you live in a swing state). Pr(you die tomorrow) = 3e-5. So Pr(your vote is decisive) is (1 – 3e-5) * 1e-6, which is essentially the same as 1e-6.
I’m reminded of Google’s claim for their storage durability:
http://models.street-artists.org/2015/05/27/99-999999999-durability-of-objects-over-a-given-year/
The adequacy of a model that is based purely on vote tallies and not on things like the motivations of key Romanian, Russian, Chinese etc online spying and fraud organizations, or how many Al Qaida cells are specifically targeting terrorism attacks at the american election process, or whether certain space junk might deorbit over florida, or if there are concerted efforts in certain cities in Alabama or Missisippi to intimidate black voters, or if we have a snowstorm in Maine or whether there will be a large power outage along the west coast, or if a nuclear power plant will have a thermal excursion causing it to go offline, or if the Cascadia fault will slip wiping out Seattle, or there is a conspiracy of high powered people of the sort mentioned in the Panama papers to use Trump to undermine the legitimacy of the Republican party and he is secretly working for Clinton…
I mean we’re talking about your plot containing estimates of between 1 in a million to 1 in a billion chance of swing vote. I’m not sure I’m willing to dismiss the Illuminati theory at negligible compared to 1 in a billion
We’ve had 5 mass extinctions in 4 billion years, and you’re graphing plots of events with a 1 in a billion chance?
This is the kind of stuff that gets power plants built along the coast at Fukushima.
It’s plausible that your numbers are in the right order of magnitude for the swing states, but it rests squarely on your prior that the effect of space junk and Romanian hackers and mass food poisoning events related to a WalMart distribution center with a bad refrigeration unit is zero. Estimates from Bayesian models are … model based. Many of us have strong priors that the effect of all that other stuff you are ignoring is non-negligible compared to 1 in a million, certainly compared to 1/billion.
Daniel:
I agree that the numbers in the 1e-9 range are speculative and model dependent. But I think the 1e-6 numbers are pretty solid, as you can derive them in other ways just by counting the number of realistic possibilities for the election outcome in any state.
I think it’s a good opportunity to reflect on the fact that Bayesian probabilities are actually about *states of information* based on the concept that the election will be orderly and no active fraud is happening, and no extreme events will occur, and you can model the vote tallies in each state based on recent polling information and high quality corrections based on party ID etc, you will get one set of numbers. But, a person who is actively involved in a fraud scheme and knows the details of that scheme would create totally different numbers. BOTH are right, relative to their state of knowledge.
You should also go vote for all the local ballot issues. I’ll be voting on a state tax issue and people in the town next to me will be voting on if they should be allowed to vote for who is on the local school board, for example. There is a higher chance of your vote being decisive on matters like those, and they can be perfectly selfish. While you’re there, you might as well take the extra second to punch a button on the president.
What do you think of Sam Wang’s model at Princeton consortium? He did pretty well in the last election.
Cugrad:
I’m glad Wang did this because it’s good to have lots of different people looking at the polls. But it’s hard for me to evaluate his method because I didn’t see a single description of his procedure and his code. It might be somewhere on his website but I didn’t see it. It did seem to say that he’s only using state polls. If so, I think that’s a mistake because then he’s leaving lots of information on the table. But maybe I was missing something there.
I like what Kremp is doing because it’s all in one place and all open. Thus if Wang or anyone else can suggest ways of improving Kremp’s method (which, again, is a variation on Drew Linzer’s model which is itself based on the political science literature), they can tell Kremp or even implement it directly for themselves.
As far as I’m concerned, the future is in using more information.
You can find his code here: http://election.princeton.edu/code/
He also has a recent post that goes into decisions he made for the model for this year, which goes into some detail: http://election.princeton.edu/2016/11/06/is-99-a-reasonable-probability/#more-18522
Patrick:
Thanks. Is he really only using state polls? That seems just weird to me.
I think he shared everything here:
http://election.princeton.edu/2016/08/21/sharpening-the-forecast/
http://election.princeton.edu/code/
http://election.princeton.edu/code/matlab/EV_estimator.m
http://election.princeton.edu/code/matlab/EV_prediction.m
Rob’s write-up is fun. Have to multiply the probabilities agains the potential change in outcomes associated with each candidate.
https://80000hours.org/2016/11/why-the-hour-you-spend-voting-is-the-most-socially-impactful-of-all/
I think that this site is a good place to air my slightly off topic bugbear. Since voting is done by people and not by acreage, it bothers me to see geographical representations of our political processes. Montana looks huge on this map, but it has only three electoral votes while Connecticut with seven votes looks tiny. There has to be a better way to represent the data.
BTW, I love Montana and Montanans.
Maps with states’ map areas adjusted proportionate to population (or electoral votes) would indeed be interesting and informative. I believe I recall seeing such maps for countries (by population, I think) somewhere, but don’t recall where.
Both 538 (in projects if you scroll down)and the NYT’s upshot (did an article on this a week ago) have versions of this. Upshot article: http://www.nytimes.com/interactive/2016/11/01/upshot/many-ways-to-map-election-results.html?rref=collection%2Fsectioncollection%2Fupshot&action=click&contentCollection=upshot®ion=stream&module=stream_unit&version=latest&contentPlacement=6&pgtype=sectionfront&_r=0
See this paper; on arXiv here. It has a population-density-distorted map for 2000’s presidential data (Fig. 3). I don’t know if there’s a simple tool for visualizing arbitrary datasets with such distortions. I agree it would be neat to see this sort of thing more often!
I think, part of the resistance to such calculation (and I include myself in this set) is a bit vague idea of what it means for one particular person’s vote being decisive. For example, ignoring cheating, miscounting and such let’s say New Hampshire comes down to N:N+1 vote split. Then every voter and potential voter in NH may claim that her personal decision made a difference, which makes it 2N+1+M people (M people didn’t vote, though they were allowed to).
Of course. If someone’s individual vote is pivotal, everyone’s vote is pivotal. If not, no one’s is.
I have more trouble with pivotality wrt courts, which would be triggered when it’s too close. Though I suppose it must be true, the hard threshold must exist, I have real trouble accepting that, say, there is a world in which it goes to the courts but it wouldn’t have gone to the courts if only the margin had been greater by 1 vote.
And then there’s the stuff Daniel Lakeland has brought up above.
It’s very hard to even conceive of the event of being decisive in a huge election.
Your intuition that multiple voters are pivotal is correct, but your analysis isn’t exactly correct.
If it comes to a N:N+1 vote split, with M people not voting even though they could, then
▪ Any of the N+1 voters was pivotal, as you correctly note. That’s because if any of these voters abstained, the result would instead have been a tie.
▪ However, none of the N voters were pivotal. That’s because if any one of these N voters didn’t vote, the result would still be exactly the same (the candidate who’s winning still wins).
▪ As for the M voters, say x would’ve voted for the losing candidate and M-x would’ve voted for the winning candidate. Then by similar reasoning, any of the x voters would’ve been pivotal had they cast their vote, because they would’ve created a tie. In contrast, none of the M-x voters would’ve been pivotal had they cast their vote, because even with their vote, the same candidate would still win.
Altogether then, only N+1 voters were pivotal. And if you want to count also those voters who could’ve voted but didn’t, then N+1+M-x voters were pivotal.
Note: The analysis is slightly different if it comes to a N:N vote. In that case, everyone is indeed pivotal.
Our local newspaper reported today that most states allow citizens to carry firearms (including open carry in many instances) to voting places. Has anyone tried to estimate the probability that a voter will be shot on the way to or from (or while in the act of) voting?
Perhaps a bit late for 2016 now but you could park it in your research plans for 2020 as it should be a good bet for newsworthiness, TED talks etc.
Well, based on background info on concealed carry permit holders, if someone is shot on the way to a polling place, it’s orders of magnitude more likely they were shot by a criminal trying to rob them or as part of drug or gang related activity, or by someone without a carry permit committing some kind of voter intimidation, than that they were shot by a concealed carry holder committing a crime. Carry permit holders commit crimes at way lower than the overall average for citizens.
Approximate numbers I’ve seen are something like 4000 crimes per 100,000 people per year in the general population, and 20/100000/yr among concealed carry holders.
if you slice it differently (based on say violent crimes, or gun related crimes, or whatever) you can probably wiggle the estimates around, but as a baseline 4000/20 = 200 times more likely to have a random general population member commit a crime than a random carry holder. Even if you somehow slice this along violent non-drug-related crimes causing injury or something and you could maybe make the ratio as low as 50:1 or something (I just made that number up) it’s still way more likely that the crime was committed by a non-carry-holder. Also, carry holders are about 6% of the population… so
p(carry holder | crime)/ p(non carry holder | crime) = p(crime | carry holder) p(carry holder)/p(crime) / ( p(crime | non carry holder) p(non carry holder)/p(crime))
the p(crime) cancels. p(carry holder) ~ 0.06 and p(non carry holder) ~ .94
p(crime | carry holder)/p(crime | non carry holder) we are estimating at 1/50 to 1/200
so the overall ratio is 1/50 * .06/.94 = 0.00128 down to 1/200 * .06/.94 = .00032 or 1/ those numbers = somewhere in the range 781 to 3125 times more likely to be a non carry holder than a carry holder.
….>
If a single honest vote could decide an election — then a single dishonest/phony vote could decide an election.
The mundane voting process matters greatly.
The emphasis here upon a single vote being valuable seems primarily subjective wheedling to bolster the reflexively assumed legitimacy of “elected” American government. The underlying story line:
‘Your vote really counts (or could really count)– and since every vote really counts — then elections are really important & really represent the will of the people… and we all should therefore really support our government that is ultimately delivered by that really good election system’.
Doubts/questions about that election system’s practical accuracy /legitimacy must be promptly dismissed as unreasonable, insignificant gray areas, or contrary to theory.
My main contention is that a 1 in a million (best chance) odd of your vote counting is just not enough motivation to make people invest much time or energy in staying informed. Contrast this with the incentives special interests have, and the return on time and energy they receive and you see why democracy will always trend towards benefiting special interests at the expense of the electorate.