Daniel Hawkins pointed me to a post by Kevin Drum entitled, “Crime in St. Louis: It’s Lead, Baby, Lead,” and the associated research article by Brian Boutwell, Erik Nelson, Brett Emo, Michael Vaughn, Mario Schootman, Richard Rosenfeld, Roger Lewis, “The intersection of aggregate-level lead exposure and crime.”
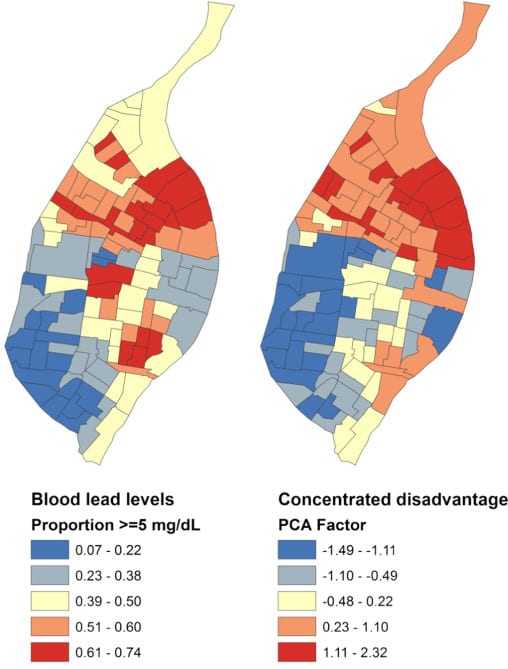
The short story is that the areas of St. Louis with more crime and poverty, had higher lead levels (as measured from kids in the city who were tested for lead in their blood).
Here’s their summary:

I had a bit of a skeptical reaction—not about the effects of lead, I have no idea about that—but on the statistics. Looking at those maps above, the total number of data points is not large, and those two predictors are so highly correlated, I’m surprised that they’re finding what seem to be such unambiguous effects. In the abstract it says n=459,645 blood measurements and n=490,433 crimes, but for the purpose of the regression, n is the number of census tracts in their dataset, about 100.
So I contacted the authors of the paper and one of them, Erik Nelson, did some analyses for me.
First he ran the basic regression—no Poisson, no spatial tricks, just regression of log crime rate on lead exposure and index of social/economic disadvantage. Data are at the census tract level, and lead exposure is the proportion of kids’ lead measurements from that census tract that were over some threshold. I think I’d prefer a continuous measure but that will do for now.
In this simple regression, the coefficient for lead exposure was large and statistically significant.
Then I asked for a scatterplot: log crime rate vs. lead exposure, indicating census tracts with three colors tied to the terciles of disadvantage.
And here it is:
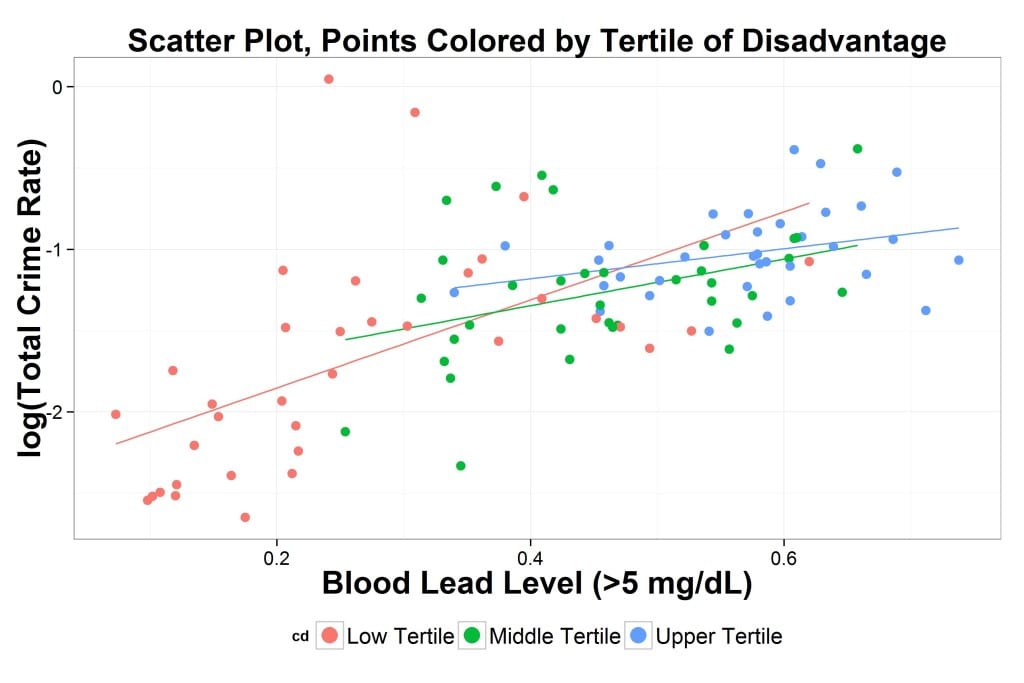
He also fit a separate regression line for each tercile of disadvantage.
As you can see, the relation between lead and crime is strong, especially for census tracts with less disadvantage.
Erik also made separate plots for violent and non-violent crimes. They look pretty similar:
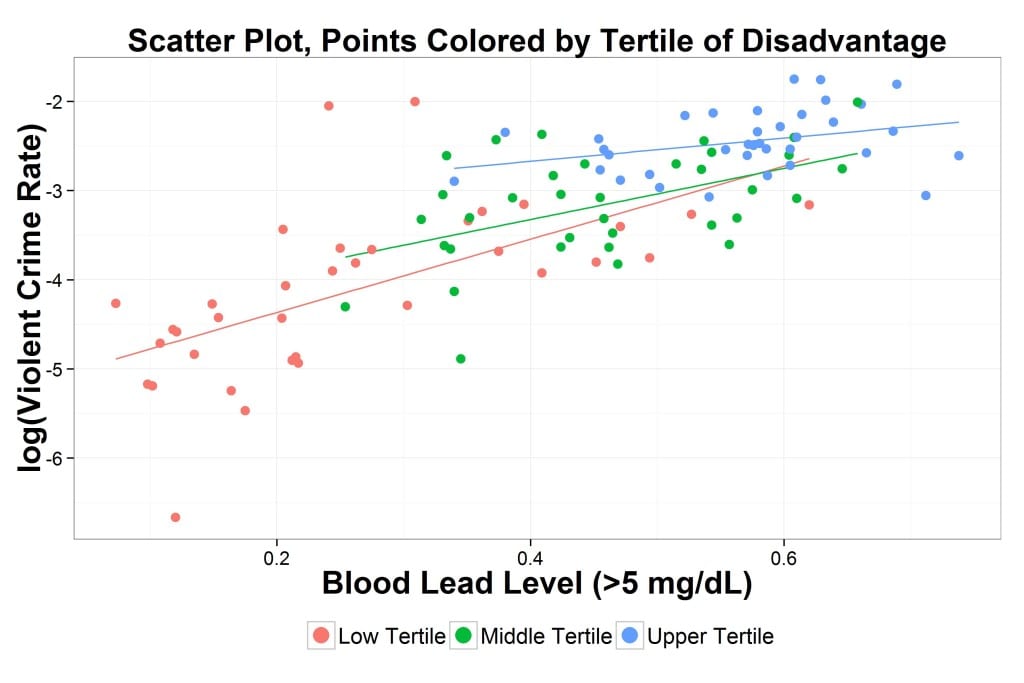
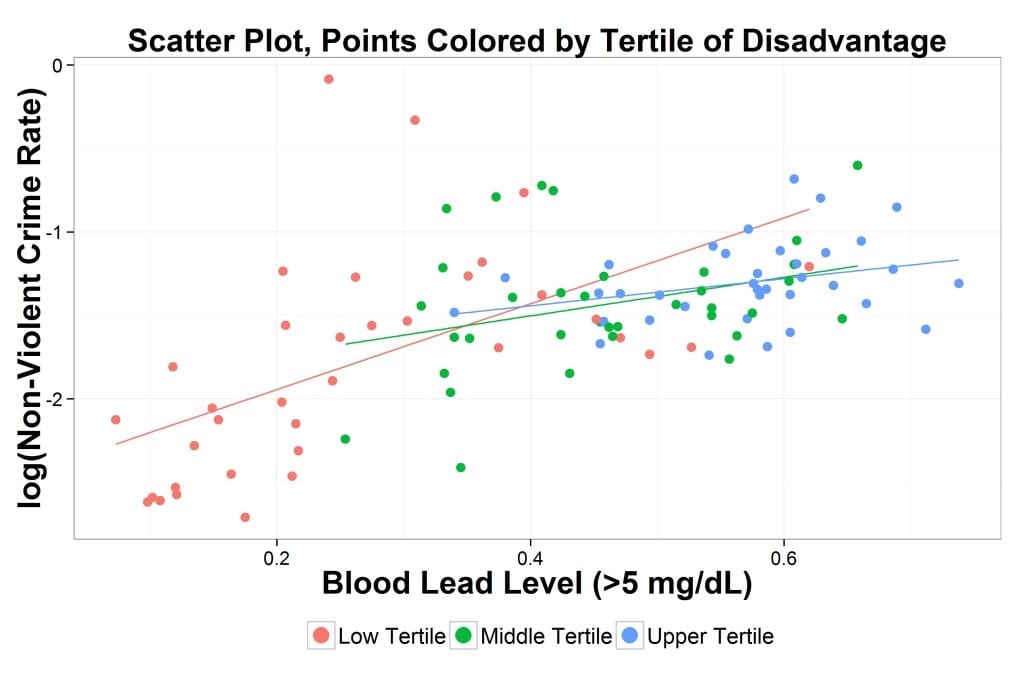
In summary: the data are what they are. The correlation seems real, not just an artifact of a particular regression specification. It’s all observational so we shouldn’t overinterpret it, but the pattern seems worth sharing.
Isn’t the most likely interpretation, by far, that lead levels are high in poor areas, as is crime? Causality matters.
David:
They do control for poverty (“concentrated disadvantage”) in their model. That said, sure, I’d expect that if you were to control for relevant unmeasured covariates that the coefficient would go down further. Still, I think that to consider causal explanations it is helpful to know what is happening in the data, hence my conclusion, “The correlation seems real . . . It’s all observational so we shouldn’t overinterpret it . . . the pattern seems worth sharing.”
Concentrated disadvantage is more than poverty and the ways in which it is more than poverty heighten its effects. I think this is good, it is a concept I have used a lot, but it’s important to know that, for example, a high poverty rural area is probably going to have lower disadvantage than a high poverty urban area, partly because it usually includes a measure of racial segregation.
Or put another way is lead part of concentrated disadvantage? The concentrated disadvantage idea is that there are so many characteristics that cause disadvantage concentrated together that they overwhelm the ability of the area to cope with them. If lead is your only problem, yeah it will make things worse. But if your area is already high poverty, high joblessness, high single parent families, highly segregated it’s just one more thing and not so much impact.
As you say, “it’s all observational so we shouldn’t overinterpret it” but the authors make additional and unnecessary modeling decisions that make it even harder to interpret. For example, the lead data is from kids under 72 months from 1996 – 2007 and the crime data is from 2008-2010. That means that the average kid in the lead data is just 10 years old at the time of the crimes. There’s a similar question about the concentrated disadvantage.
(I wouldn’t be surprised if these aggregate statistics are all stable (in relative terms) over time, in which case the results would be unaffected.)
The other big issue to which they devote just one sentence is mobility: people commit crimes outside of the census tract they were born in.
> We should also note that the inclusion of a measure intended to assess residential mobility [i.e., in-out migration measured via length of home ownership] failed to alter our findings substantively.” But I’m guessing that the majority of poisoned kids’ families are renters not owners.
I would guess that a large number of poisoned kids’ families are renters, not owners?
(Typo: crime data is from 2010-2012.)
There’s been a lot of work on the relationship between lead and crime. The most striking observation is the drop in crime after lead is removed — the same pattern is observed in different states and countries that removed lead from petrol (gasoline) at different times.
Yeah, Rick Nevin has done a lot of work and has links to other people who have done work in this area.
There is non-sociologial data to confirm the link, of course. We know from neurobiology *what* many of the effects of lead poisoning in early childhood *are*. They include low intelligence and poor impulse control. We also know what the effects of severe lead poisoning are, and they include violence and paranoia.
We would expect violent, paranoid people with low intelligence and poor impulse control to commit more crimes, right?
So neurobiologically we should expect lead poisoning to make more people into criminals.
I actually think based on eyeballing that the violent and non violent crimes (which will mainly be drug offenses) look pretty different and for the low tertile plots the influence of high blood levels is being leveraged towards 0 by a small number of very high lead level places that have lower than expected crime numbers.
Also I want to mention something important to understand about small place crime numbers. The address where crimes are reported is not necessarily the address where the crime took place, and it is certainly the case that it is not the same address as the offender. Many, many crimes are actually reported at police stations and more violent crimes in particular are reported at hospitals where a victim shows up. Other crimes take place in parks, which are low population, high crime locations which often are their own census tracts. So you must always exercise extreme caution in understanding the tracts that you are analyzing and what the addresses mean. People generally do not travel far for committing crime, so their home census tract may be near the hospital or the police station, but that calls for some integration of spatial relationships.
Thank you for this analysis Andrew.
Something to note: African-Americans are concentrated in the northern part of the city and also in the areas that are in the upper tertile of concentrated disadvantage. As you can see in the graph, these areas are where the lead-crime slope was the flattest. So while the statistical correlation holds up, it does *not* seem to be a great explanation for the decline in African American crime, which was the the driving force in the crime spike during the 1990s.
As significant as the lead-crime connection is, I’m now much more wary of using it to explain the decline of crime since the 1990s, unless I’m misunderstanding the graph.
(Maybe I haven’t learned anything from reading this blog if I have just eyeballed a graph and told a story to explain a correlation away! But my point is that if people like Drum are going to make the bold claim that lead drop was responsible for the specific 90s crime drop, we should be careful to check if it’s consistent with this evidence.)
It seems likely to me that lead causes crime.
But suppose that lead and other, social disadvantages are correlated, as we believe to be true. Suppose also that social disadvantage were, like lead level, measured as a numeric variable with many possible values. And further suppose the opposite of what you believe: that with lead and social disadvantage as two independent variables, social disadvantage is correlated with crime, but lead level does not correlate with crime.
Even under the above conditions, if you then took the social disadvantage numeric value and grouped it into just 3 categories (as in your scatter graph), you would expect to see a spurious correlation between lead and crime, because within each disadvantage category, the varying exact level of disadvantage would correlate with lead level.
This is similar to the problem with a claim that some stat has seen an “age-adjusted” trend, but where the ages are divided into a few groups, instead of expressed as an exact age.
I don’t have access to the original paper, but I’m almost certain that you meant 5µg/dL (micrograms), not 5mg/dL (milligrams) on your image axes and legends.
I went to school from K to 12 in Sherman Oaks, CA, which had the busiest freeway interchange in America (101 Ventury / 405 San Diego freeways) in the 1960s and 1970s. It would be interesting to see if crime was higher among white middle class kids in Sherman Oaks than in places further away from traffic jams.
For White middle-class kids, you’d probably need some other measure than crime for the effect of lead on impulse-control, intelligence, and violence.
What about a measure like expressing racist views on the internet?
Why would that be the case?
Because reported crime rates are so low for middle-class white youths that it would be hard to detect an increase. This is probably both because they commit fewer crimes (e.g., they have less temptation to steal, since they are not suffering material deprivation), and because their parents are often able to keep them out of the criminal justice system when they commit crimes such as hazing and bullying, whereas poor and minority children are more likely to be arrested.
That doesn’t sound right. You’re asserting that there are more arrests per crime committed in black neighborhoods than in white neighborhoods?
He is actually saying that conditional on arrest, there is an increased likelihood of a criminal record.
well if he’s not saying that there are more arrests per crime reported in black neighborhoods than white neighborhoods his point goes out the window.
ziel:
David is saying two things:
First, he argued that there is a differential probability of being put into the criminal justice system, which can be characterized as Pr(Prosecution | Arrest). Second, he made the argument that there is differential probability of being arrested, which can be characterized as Pr(Arrest | Caught).
I don’t think David is making an assertion about Pr(Arrest | Crime Committed). However, he can certainly correct me if I am misstating his position.
1) The scatter graph is on reported crimes, not arrests or prosecutions.
2) My comment, like the one which started this thread, was specifically about middle-class white youths and their crimes, not just white neighborhoods vs. black neighborhoods. (I didn’t think it was fair to assume that Jay Livingston was being racist, when his position was consistent with all sorts of views on race, including that of liberal black activists.)
3) Middle class white “parents are often able to keep [their children] out of the criminal justice system” because they may be better treated by victims and authorities, can advocate or hire lawyers to advocate for alternative resolution, can pay for damages, and can pay for “therapy” or psychiatric interventions as an alternative resolution, all of which may keep a crime from even being reported.
4) I thought my earlier comment about the logical flaw in the scatter graph of tertiles was a lot more interesting, but I suppose I could have written it in a more compelling fashion.
Of course, that’s well known. For example pot use is similar for white and African American teens but African American teens are way more likely to end up in contact with the CJ system.
From my experience with several high crime cities, it seems like only a tiny fraction of the crime ends up getting reported, much less investigated and prosecuted. In nice areas, in contrast, neighbors will complain if you leave your trash cans out or if your grass is too high or your shutters are the wrong color.
You have a point. So does gregor. I don’t know how the Pr(Criminal Report | Crime Committed) works out altogether. But another factor is when crimes in a middle-class census tract are low, a larger portion of them should be expected to be due to people coming in who live in other census tracts (each tract is only about 1 square kilometer), and so the effects of lead on the local population will be harder to sort out.
from the physiologic perspective:
https://www.atsdr.cdc.gov/csem/csem.asp?csem=7&po=10