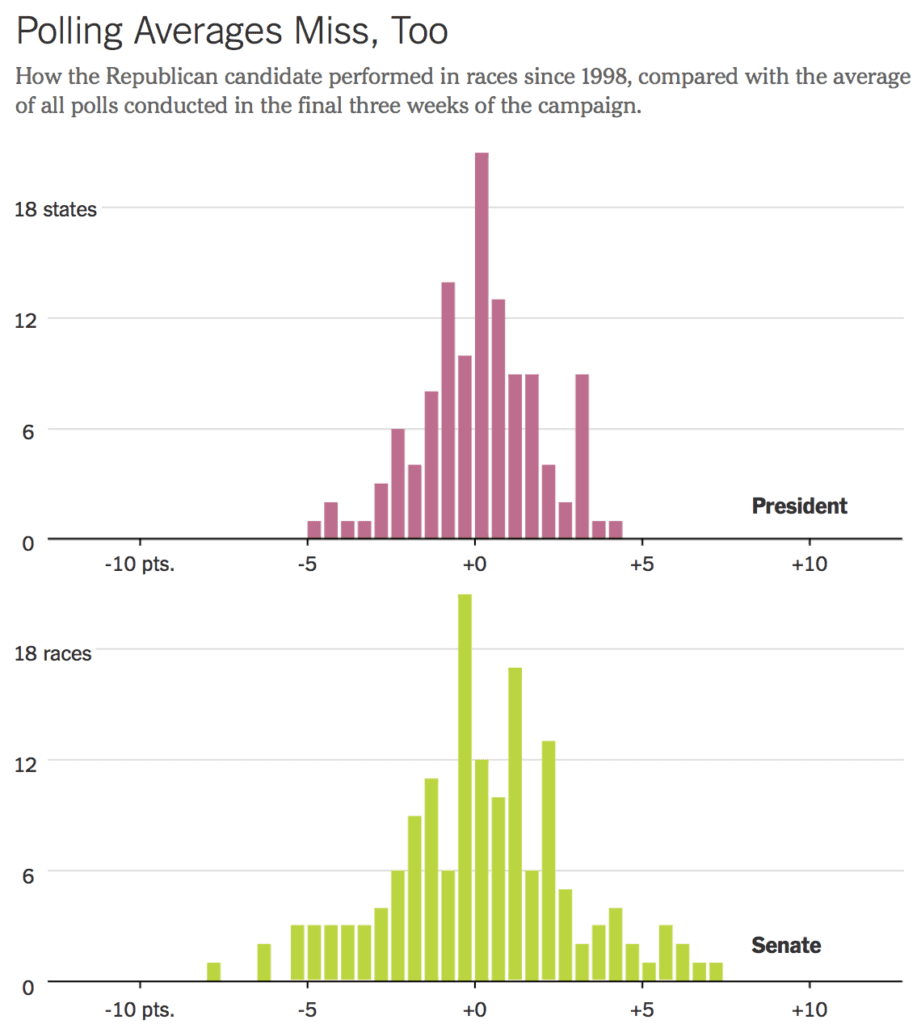
David Rothschild and Sharad Goel write:
In a new paper with Andrew Gelman and Houshmand Shirani-Mehr, we examined 4,221 late-campaign polls — every public poll we could find — for 608 state-level presidential, Senate and governor’s races between 1998 and 2014. Comparing those polls’ results with actual electoral results, we find the historical margin of error is plus or minus six to seven percentage points. . . .
Systematic errors imply that these problems persist, to a lesser extent, in poll averaging, as shown in the above graph.
David and Sharad conclude:
This November, we would not be at all surprised to see Mrs. Clinton or Mr. Trump beat the state-by-state polling averages by about two percentage points. We just don’t know which one would do it.
Yup. 2 percentage points. They wrote this on October 6, 2016.
I wonder what the final Clinton win probability of the models would’ve been if you simply made the standard error larger by the amount suggested in your Disentangling Bias and Variance in Election Polls paper.
Anon:
I think that’s pretty much what Nate must have done, even if not explicitly using our analysis. The funny thing is, I wrote about and made calculations using Pierre-Antoine Kremp’s implementation of Drew Linzer’s forecasting model, and those models did allow for nonsampling error, but they did not actually include what we’d learned from that Disentangling paper. This happens sometimes. We work on these different research projects and don’t put them all together.
The irony is that I actually used this paper when I added a correlated polling error term to the model. If I understand Table 3 of the paper correctly, the average absolute bias of state polls in presidential elections is about 1%; this implies a standard deviation of a normally distributed polling error of 1.25% (mean(abs(rnorm(1e5, 0,.0125))) is close to .01).
On the logit scale, when scores are around 50%, that meant a standard deviation of about 0.05 (sd(inv_logit(rnorm(1e5, 0, .05))) gets you close to .0125). And because I already had pollster house effects, with an estimated sd of about 0.03, I thought I was being somewhat conservative by adding a polling error term with a standard deviation set to 0.04… I guess I was wrong.
(Of course, I could very well have misread or misinterpreted the paper).
I happened across this earlier this evening – https://mathbabe.org/2016/11/11/the-models-were-telling-us-trump-could-win/
An excerpt:
“This article by Sam Wang (Princeton Election Consortium) explains how you end up with a win probability of 98-99% for Clinton. First, he aggregates the state polls, and figures that if they’re right on average, then Clinton wins easily (with over 300 electoral votes I believe). Then he looks for a way to model the uncertainty. He asks, reasonably: what happens if the polls are all off by a given amount? And he answers the question, again reasonably: if Trump overperforms his polls by 2.6%, the election becomes a toss-up. If he overperforms by more, he’s likely to win.
But then you have to ask: how much could the polls be off by? And this is where Wang goes horribly wrong.
The uncertainty here is virtually impossible to model statistically. US presidential elections don’t happen that often, so there’s not much direct history, plus the challenges of polling are changing dramatically as fewer and fewer people are reachable via listed phone numbers. Wang does say that in the last three elections, the polls have been off by 1.3% (Bush 2004), 1.2% (Obama 2008), and 2.3% (Obama 2012). So polls being off by 2.6% doesn’t seem crazy at all.
For some inexplicable reason, however, Wang ignores what is right in front of his nose, picks a tiny standard error parameter out of the air, plugs it into his model, and basically says: well, the polls are very unlikely to be off by very much, so Clinton is 98-99% likely to win.
Always be wary of models, especially models of human behavior, that give probabilities of 98-99%. Always ask yourself: am I anywhere near 98-99% sure that my model is complete and accurate? If not, STOP, cross out your probabilities because they are meaningless, and start again.”
Chris:
I think that probabilities of 98-99% can be reasonable, but they were not in that case for the reasons that are given in my post above.
Two things caught my attention in the text quoted above:
1. The polling errors since 2004. In the context of those errors, a few percent error this year doesn’t seem crazy at all. (Consistent with your post the other day, which I hadn’t read until an hour ago.)
2. The authors comment “Am I anywhere near 98-99% sure that my model is complete and accurate?” If one has that level of confidence than hopefully it’s because the model has calibrated/cross-validated. (Calibration and cross-validation are good things.)
If you plot the data in the histograms above as deviation vs time is there any suggestion of time-dependence?