Deborah Mayo asked me some questions about that paper (“Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors”), and here’s how I responded:
I am not happy with the concepts of “power,” “type 1 error,” and “type 2 error,” because all these are defined in terms of statistical significance, which I am more and more convinced is a bad way of trying to summarize data. The concepts of Type S and Type M errors are not perfect but I think they are a step forward.
Now, one odd thing about my paper with Carlin is that it gives some tools that I recommend others use when designing and evaluating their research, but I would not typically use these tools directly myself! Because I am not wanting to summarize inference by statistical significance.
But let’s set that aside, recognizing that my paper with Carlin is intended to improve current practice which remains focused on statistical significance.
One key point of our paper is that “design analysis” considered broadly (that is, calculations or estimations of the frequency properties of statistical methods) can be useful and relevant, even _after_ the data have been gathered. This runs against usual expert advice from top statisticians. The problem is that there’s a long ugly history of researchers doing crappy “post hoc power analysis” where they perform a power calculation, using the point estimate from the data as their assumed true parameter value. This procedure can be very misleading, either by getting researchers off the hook (“sure, I didn’t get statistical significance, but that’s because I had low power”) or by encouraging overconfidence. So there’s lots of good advice in the stat literature, telling people not to do those post-hoc power analyses. What Carlin and I recommend is different in that we recommend using real prior information to posit the true parameter values.
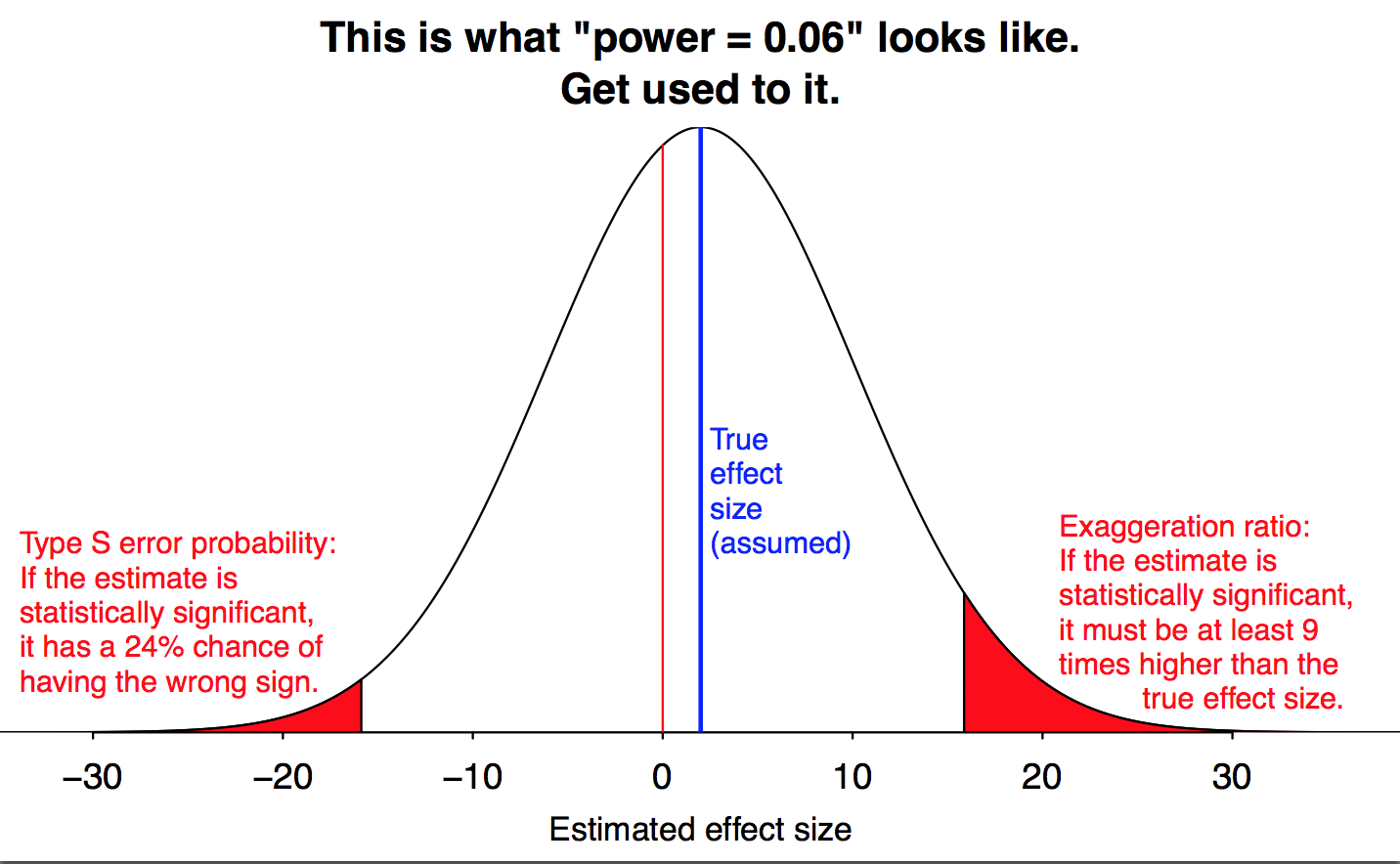
The other key point of our paper is the statistical significance filter, which we rename as the exaggeration factor. The exaggeration factor is always greater than 1, but it can be huge if the signal is much smaller than noise.
Finally, this all fits in with the garden of forking paths. If researchers were doing preregistered experiments, then in crappy “power = .06” studies, they’d only get statistical significance 6% of the time. And, sure, those 6% of cases would be disasters, but at least in the other 94% of cases, researchers would give up. But with the garden of forking paths, researchers can just about always get statistical significance, hence they come face to face with the problems that Carlin and I discuss in our paper.
I hope this background is helpful. Published papers get revised so many times that their original motivation can become obscured.
P.S. Here’s the first version of that paper. It’s from May, 2011. I didn’t realize I’d been thinking about this for such a long time!
P.P.S. In comments, Art Owen points to a recent paper of his, “Confidence intervals with control of the sign error in low power settings,” following up on some of the above ideas.
Conditional on getting a negative result, wouldn’t publication oriented researchers prefer to have had high power so that they can make a more affirmative statement that something close to the null is likely true? Otherwise, they just have nothing.
+ 1. Yes! I’ve been musing a lot lately that truly good science is done when a negative result means as much as a positive result, both statistically and scientifically…
One thing I would’ve liked to see in this paper is a discussion of this kind of design analysis in the context the opposite-type situation… you know, when you are Brian Nosek and have a replication sample of sufficient power to test some previous claim.
Suppose there is a literature out there that says “the effect of X on Y is Beta”, but anyone without a Ph.D. could tell you that Beta was an over-estimate (unfortunately, assume people with a Ph.D. published it anyway). Then you come along and run a new, well-designed, well-powered experiment to estimate Beta, and get an estimate that is not statistically significant but is a) much smaller than the original; and b) has much smaller standard errors.
I’d like to be able to use this kind of design analysis to make claims about plausible values of Beta, or values of Beta we can “rule out” given the new analysis (in relation to the previous estimates). Sure, I could just say “The old estimates fall outside the 95% confidence interval of the new estimates” or “I can reject that the two estimates are the same, and mine is better measured”, but I want something a bit more. Or at least a discussion of how Type M/S errors could be used for shoring up a good analysis relative to a bad analysis. I feel like it is both an obvious question (I could calculate Type M error rates given the previous estimates as the “true” effect and see what the probability of my estimates are in that world) and a difficult one, in that we still don’t have a lot of tools for thinking about how to “over-rule” previous estimates or constrain the range of potential parameter values while having non-significantly-different-than-zero point estimates. I don’t think uncertainty (confidence) intervals are quite sufficient, or use quite enough information.
But if we are gonna go into effect size estimation instead of hypothesis testing (which we should be doing in a lot of contexts), I think we want these tools to help us compare newer, more precise estimates with older, garbage estimates. It would also give replication a new place in the literature…replication as refinement of parameter estimates, not as “proof” or “refutation”.
If only there were a theoretically well developed way to take some old estimates based on a small and relatively poor set of information, add some new data, and come up with a logically consistent new estimate that balances the two sources of information. Perhaps we could pray that such a method might be developed and then made broadly available under the name of some religious leader, a reverend perhaps.
+1 :)
Daniel,
So you’d just plot some moments of a posterior distribution and say that you can rule out anything outside the tails? I get that there are some efficiency gains, but I’m not talking small-N here, and so with some reasonably flat priors wouldn’t we just get back something looking a lot like an uncertainty (confidence) interval?
My point isn’t about estimation, or even necessarily about probability calculations themselves, it is about a conceptual/rhetorical problem for researchers doing well-powered, well-measured experiments that obtain a “tight 0 effect” to confront previous under-powered, poorly-measured experiments that generated implausible (to anyone but a few academics) estimates.
Suppose, for instance, there are a whole bunch of underpowered studies mining noise around a particular question, and coming up with conflicting answers (in the GOFP way, where, like, by study 3 the effect reverses for redheads born on odd-numbered days). So you do a large-N study, and get a tightly-estimatate 0 effect across everyone. Now you want to say that none of the other estimates are plausible, and yours effectively rules them out.
How would you argue it, using a power-type argument? Would you compute exaggeration factors for the other studies? Would you test various alternative hypotheses and rule them out one after another? Would you compute your own type-M estimates using their point-estimates as references? Or would you just plot the moments of some posterior distribution and call it a day?
In part, I think that pushing on this kind of thing is a way to get better-measured, “null effect” papers published in fields full of “statistically significant noise.” I don’t think switching to Bayes really helps here. What I want is a mathematical/rhetorical framework for publishing high quality replications, and for discriminating between higher- and lower-quality replications and ones which do/don’t teach us something new about the world (even if that is just refuting something we previously thought based on poor statistical analysis).
Unrelatedly, I owe you a coffee or three…
“I don’t think switching to Bayes really helps here.”
On the other hand, that was exactly what I was suggesting in a tongue in cheek manner, switching to Bayes really DOES help here. So we might as well flesh it out a little and also I’m doing way better now that it’s fall and the grass pollen is way down so let’s get together and have some coffee etc and talk in person as well.
Now, how does Bayes help? First off, what is Bayes about? Thanks to a very clear paper from Kevin S Van Horne discussed on my blog here: http://models.street-artists.org/2016/08/16/some-comments-on-coxs-theorem/ we see basically that Bayes is the mathematics used to update “states of information” in a way consistent with the limiting case of perfect information, namely Boolean binary logic. At the very end of the paper, he takes “state of information” to *be* probability distributions for the purpose of formal set/model-theoretic proof of consistency (basically, Bayes is a consistent theory because it maps one-to-one to the math of Kolmogorov measure theoretic probability theory)
Fine, basically we work with probability distributions over the possible values of certain quantities in the world, taken as measures of the “plausibility” that a given value is the real value in the world rather than the frequency with which that value is obtained in sampling (the same concept used in your phrase ” Now you want to say that none of the other estimates are plausible, and yours effectively rules them out. “)
So, we start with some weak sauce from the field, taken as GOFP p-value ridden estimates of “effect sizes” as the average over their dataset conditional on the fact that they decided they could publish it after testing some stuff with the Morgan-Rosenthal-Trappman-test-of-goodness-of-publication… Note, whatever calculations they’ve done via NHST do not really leave us in a “state of information” in which we need to buy into their effect size estimates because they are NOT equivalent to Bayesian calculations. Nevertheless, we do have SOME information from the published data. So, we need to start somewhere, and it’s best if we can get their data and soforth, but often we’ll probably have to start with a prior constructed as a “hedge” against GOFP/hacking/biases and general noise-mining. So, for example we might use a power calculation to back out a graph like the one at the top of this post and use that as a prior.
Next, we look at the large well designed replication. If we’ve done a good job of designing the replication we can write down relatively easily a likelihood based on the well specified design (whereas one of the things that GOFP could be taken to mean is that when NHST + significance filtering + choice of test + etc etc is all taken into account, it’s pretty hard to describe a meaningful likelihood. On the other hand, in the replication, the likelihood is probably a lot easier to decide on.
Now, combining the likelihood from the well specified replication design, and the hedge prior that uses the published original results as a more or less order of magnitude type estimate… you arrive at the end with a relatively tightly concentrated posterior distribution thanks to your posited well designed high powered replication… and this posterior either includes the original estimated effect sizes in its high posterior probability region, or it doesn’t.
Any other method for narrowing down the interval of plausible values will fail to meet one of the desirable properties posited by Cox’s theorem, ie. will fail to agree with Boolean logic for example. So, I really think the way to look at replications is to do them as a Bayesian update with the existing poorly informed literature as a guide to the order of magnitude (for example, suppose someone suggests there’s a 3% difference in such and such based on GOFP/NHST/small samples/noise/storytime)… then a prior normal(0,10%) seems like a good starting point, it includes all the values within a small multiple of the effect size from the literature and includes both directions.
So, yes, I really do think Bayes is the way to go for high quality replications.
Now, when it comes to actually fleshing out issues at the core of the basic model (ie. where the effect itself may not be even a well-specified or well thought out thing, or the measurement may have very little connection to the effect compared to what the field thinks… etc) then that’s a different story, still a Bayesian story in my opinion, but now you have to do some kind of model choice or model averaging or something.
Daniel, you suggest that the experimental design features that might be described as p-hacking affect the likelihood function, but that doesn’t seem to be entirely accurate. Surely the likelihood function is entirely fixed by the data and the statistical model, and in that case it is unaffected by the significance filter (and “etc”?).
Michael:
With p-hacking or forking paths, the statistical model chosen to analyze the data is itself a function of the data, hence the likelihood principle in its usual formulation does not apply.
To a Bayesian “likelihood” p(D | P, X) is a measure of “how plausible is it that data would look like D if parameters looked like P and the world works in the way that model X suggests”
Now, the summary statistics and p values computed by the researcher are themselves DATA to the Bayesian. So we need to assign some plausibilities to these statistics and p values (ie. 4% of red headed women over 50 years of age with more than 1 child reported feeling uncomfortable when shown pictures of hairless monkeys, or whatever strange interactions tend to come up in these p hacking experiences).
which X should we use? that is, how did the data, including the choice of summary statistics and test statistics and hypotheses to test etc actually arise?
We can’t generally figure out how to assign plausibilities to the data D when D includes the output of the original researchers research choices.
Let’s not forget about the part where we may have no universally plausible likelihood model just for the direct measurements involved, especially when the measurements involved constructed scales or people responding to vague survey questions or whatever. (on a scale of 1 to 10 how bad is your pain right now? https://xkcd.com/883/)
Here’s one technical reference I know of Dawid, A. P., and Dickey, J. M. Likelihood and Bayesian inference from selectively reported data. Journal of the American Statistical Association 72 (1977), 845-850
> a theoretically well developed way to take some old estimates based on a small and relatively poor set of information
So when one is unsure of selectivity and other poor research practices it is not practically feasible.
Without those problems the summary observed (or reported) likelihood is just an integral over probability of individual level data that could have resulted in the summaries – if interested see https://phaneron0.files.wordpress.com/2015/08/thesisreprint.pdf
Keith:
I haven’t looked at this paper but my guess is that it won’t do the job. I say this because it seems to me that file-drawer is the least important form of selection bias, so correcting for file drawer won’t begin to correct for garden of forking paths. Indeed, one problem I’ve had with file-drawer analyses is that it can give researchers a false sense of security.
Keith, Andrew,
In the context of a new and substantially well-designed replication type study with open-data access and all that yummy sauce, where we’re looking to the previously published estimates for some kind of order-of-magnitude approximation for diffuse priors, it seems to me we don’t need to be that demanding on the interpretation of the published estimates or have a good likelihood function for them.
On the other hand, where all we have is the published estimates and no new replication study, and we’re trying to do meta-analysis on the studies themselves, then I agree with Andrew’s concern about biases other than file drawer, and Keith’s statement that “when one is unsure of selectivity and other poor research practices, it is not practically feasible”
Taking some summary statistics and some p values as the “output data” from some selective and poorly analyzed NHST based everything goes GOFP gotta get something published to get the next grant accepted… you can’t really design a likelihood that would inform you about the real effect.
Andrew: Unfortunately I don’t have access to the Dawid paper this morning but my recollection (from 10+ years ago) was that it was more about garden of forking paths. My interest was in how it accounted for the choice of summary reported in a paper and summary could be any particular analysis chosen to be reported in the paper to the exclusion of others.
From my thesis it was described “The alternative formulation of the likelihood-based on the distribution of the summary reported and the fact that the summary was chosen to be reported on the basis” of that summary being liked for some reason by the authors.
But given one would seldom know much about that, the formulation was not not practically feasible.
also note, I’m thinking of the general case in which we may not be able to get more than a few summary statistics and p values published in an article out of the original researcher, rather than the ideal case where we could grab their whole data set and ignore their choice of tests, and analyze the full raw combined datasets of the original plus whatever replication there was.
Daniel – As stated in the comments on your blog I continue to believe that most Jaynesians (including Jaynes) misunderstand the content and implications of Cox’s theorem. It seems to be used as a form of pseudo rigor followed by massive hand waving.
Interesting, what aspect of the interpretation of cox’s theorem are you dissatisfied with?
I was very happy for the opportunity to go deeper into the implications in those blog comments, but I came out of it thinking basically what I thought going in, just with a better understanding of the boundary cases. I’ve always always always advocated the position that the creative model building aspect is REALLY important, and it’s pre-Bayesian and it does a lot of heavy lifting in science, and I think this is at least some of what you were concerned about. You can’t use Bayes to come up with models, you can only use it to distinguish between plausibilities under one or more models. But, in this case, JRC was explicitly asking about how to figure out what was and wasn’t plausible after seeing a bunch of data… and this is explicitly what Bayes is about under Cox’s axioms.
My thought exactly. The give-away is in footnote 4:
“4. A more direct probability calculation can be performed with
a Bayesian approach; however, in the present article, we are
emphasizing the gains that are possible using prior information
without necessarily using Bayesian inference.”
There is nothing wrong with this paper. But it still makes me want to bang my head against a wall. Why is it necessary to hold peoples hands in this way and present them with such a kindergarten approach? Are there really scientists out there (scientists!) who are happy to make a point-estimate prior (for that is what Andrew’s “assumed true effects” are), and be taken step-by-step through the consequences for the p-value calculation, but are not able to grasp that you might assign a probability distribution to a whole range of “assumed true effects” based upon the kind of plausibility argument presented in the paper? At what point do they throw their hands in the air and say “Noooo! Those probabilities can’t be interpreted as frequencies, it makes my head hurt!”
The footnote shows Andrew knows exactly what he is doing. But why? P-values are rubbish. Statistical “power” is rubbish. And “unbiased estimators”, and all the rest of the baggage. So why carry on teaching it?
Put everything you know before the experiment into the prior. Then Bayes in the results. Then everything you know after the experiment is in the posterior distribution, including of course the “S-type” and “M-type” errors. Simples. The posterior will tell you that if the effect you appear to have seen is implausibly large (compared to the prior) then, whatever the p-value, you probably have abserved a fluke (or cherry-picked) event.
I told my first year applied stat class about this example, along with Youden’s sequence of confidence intervals for the astronomical unit. (Technometrics, 1972).
The figure in Andrew’s post describes something like 5.5ish percent power. Six percent power gives you about 20% wrong signs (conditionally on rejection) and a minimum exaggeration of about 6.65 fold (not 9). So clearly the main point that low power has severe consequences holds up.
Andrew’s post surprised me because I had been taught that while the point null is seldom plausible, rejecting it means you can be confident about the sign. Now it just looks like not rejecting it means you do not know the sign. There is weird middle zone where you can reject H_0 while having no great assurance about the sign.
See the arXiv paper below for the details in the asymptotically normal case. It is all elementary math, but to me at least, a time for thinking slow instead of thinking fast. One-sided tests and confidence intervals appear to make the problem worse.
If the confidence interval has some decent separation from 0 (in units of its own width), then you can be confident about the sign. That is like being able to also reject the null at a second, more stringent, level.
It would be great to have some posterior probability for the sign. A prior on the effect size should be enough to do it. Choosing a prior on effect size looks too much like a researcher degree of freedom to me (others will disagree). Maybe the recent progress on conditional inference will provide a good alternative. I suspect (no proof) that the conditional inference approach will also need to bring in something from outside the data. The CLT does not leave you with a lot of parameters to work with.
https://arxiv.org/abs/1610.10028
I like the M and S (sounds better than the other way around) framework for continuous dependent variables, where effect size is crucial. But what about binary situations? Doesn’t the Type I and II error framework apply there?
Peter:
The problems I’ve seen are not binary: the interesting question is not whether an effect is exactly zero, but rather how large is the effect, how much does it vary, where is it high and where is it low, etc.
In Genetics, we name the exaggeration factor as Beavis effect after Beavis (1994, 1998), who showed that significant quantitative trait loci from genome scans are often overestimated in typical datasets. Xu (2003) gives a nice overview from genetics perspective (http://www.genetics.org/content/165/4/2259).
Yeah hehehe… hehehe… yeah…. trait loci rule. hehe. yeah.
https://memegenerator.net/instance/70393369
#BestCommentSection