This post is by Phil Price, not Andrew.
Before I get to my question, you need some background.
The amount of electricity that is provided by an electric utility at a given time is called the “electric load”, and the time series of electric load is called the “load shape.” Figure 1 (which is labeled Figure 2 and is taken from a report by Scottmadden Management Consultants) shows the load shape for all of California for one March day from each of the past six years (in this case, the day with the lowest peak electric load). Note that the y-axis does not start at zero.
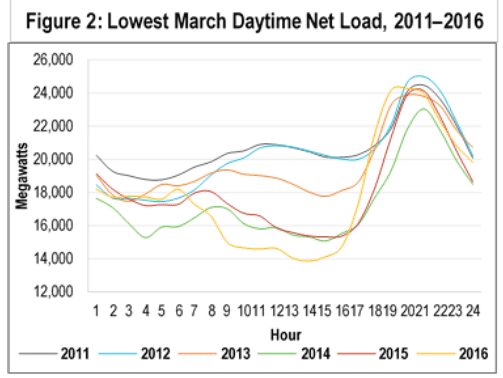
Figure 1: Electric load (the amount of electricity provided by the electric grid) in the middle of the day has been decreasing year by year in California as alternative energy sources (mostly solar) are added.
In March in California, the peak demand is in the evening, when people are at home with their lights on, watching television and cooking dinner and so on.
An important feature of Figure 1 is that the electric load around midnight (far left and far right of the plot) is rather stable from year to year, and from day to day within a month, but the load in the middle of the day has been decreasing every year. The resulting figure is called the “duck curve”: see the duck’s tail at the left, body in the middle, and head/bill at the right?
The decrease in the middle of the day is due in part to photovoltaic (PV) generation, which has been increasing yearly and is expected to continue to increase in the future: when the sun is out, the PV panels on my house provide most of the electricity my house uses, so the load that has to be met by the utility is lower now than before we got PV.
Other technologies also change the load shape. For example, electric vehicle charging will cause increases in mid-morning as people charge their cars after driving to work, and in the evening as they charge them when they return home. “Time-of-use” electric rates, in which the charge for electricity depends not just on the amount that is used but also on when it was used, will get people and businesses to shift some of their loads to off-peak periods.
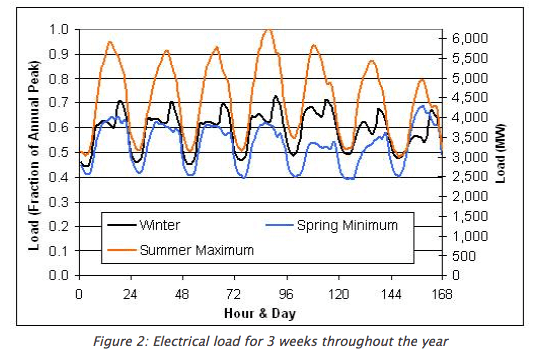
There are large weather-related changes to the load shape. On a hot summer day the peak is usually some time in the mid-afternoon, when home and commercial air conditioners are working hard. Figure 2 (which is from a UC Boulder class website and I presume shows Colorado, not California) shows how the load shape can change with season.
Electric utilities need to set electric rates now, and also to plan for the future. For instance, the annual peak load — the highest system-wide load reached in the entire year — is a very important parameter because both the generation and transmission systems must be able to meet the demand. Installing giant transformers and transmission lines everywhere would be wasteful and expensive, but if they are under-sized compared to future needs then they will need to be supplemented or replaced, which is also wasteful and expensive.
Naturally, utilities are very interested in how the load shape is changing, and in forecasting how (and why) it will change in the future. As part of that forecasting, they are interested in quantifying how things are changing already: when do people charge their electric vehicles? How much do rooftop solar installations contribute throughout the day and the year (this of course depends on the orientation of the roofs, and how and when they are shaded, and so on). Even if they knew exactly what is happening now, this wouldn’t be sufficient to make an accurate forecast: electric vehicles will continue to increase in battery capacity, the roofs on which solar panels are installed will differ from those that have already installed them, and so on. But one has to start somewhere.
When the technology of interest is a generating technology it is possible in principle to directly monitor it: one can install a meter that measures the load of the electric vehicle charger on its own, for instance. But installing a meter is expensive; and even when meters exist the data may not be available to the utility but only to the system installer and the customer (this is a common case with solar panels). And when trying to evaluate the effect of something that doesn’t generate power, such as time-of-use metering, there is no way to directly meter the change, even in principle. In these cases, there are two basic approaches: (1) a before-and-after comparison (this is called pre/post analysis) and (2) a case-control study.
In a pre/post analysis, one creates a statistical model that fits the load data from before the new system or policy was installed, and uses it to predict the load afterwards. This is compared to the actual load afterwards, and the difference is quantified. For instance, one could create a statistical model to predict the peak load, given the afternoon outdoor air temperature and the day of the week, and fit the model to data from before the building went onto a time-of-use metering plan. This model could be used to predict what the peaks would have been in subsequent weeks if the building had remained on its original rate plan. These predictions can be compared to the actual peaks.
Pre/post analysis usually works pretty well if the “post” period is fairly short — a few months, say. After that it gets increasingly uncertain because buildings tend to change: the tenant on the third floor moves out, the retail shop on the ground floor changes its operating hours, etc. So if time periods of interest are a long way apart — comparing this summer to last summer — a pre/post analysis is subject to a lot of uncertainty. Still, this is the standard approach to quantifying changes.
Fortunately, utilities, including my client, usually don’t care all that much about any individual building. They are interested in large portfolios: “What was the effect of switching 5,000 small commercial customers in a specific region onto a particular time-of-use rate plan last year?” Aggregation obviously helps enormously: tenants move out of some buildings but into others, some businesses increase their operating hours but others decrease them, etc. But even with aggregation, pre/post analysis has some problems. For one thing, a change in the local economy can raise or lower all the boats, compared to the model prediction: fewer vacancies, more workers in office buildings, longer operating hours. For another, changes in technology (such as gradually switching from fluorescent to LED lighting, or from desktop to laptop computers) can lead to a modest but non-negligible change in load in most buildings, on a timescale of a few years.
An alternative to pre/post analysis is case/control analysis: Match those 5,000 small commercial customers who switched rate plans with 5,000 (or even 50,000) who did not. If you do the selection so that the average load shapes of the cases was the same as the controls prior to going onto time-of-use metering (or prior to getting electric vehicle chargers, or prior to getting solar panels, or whatever), then you can compare the cases to the controls later on, and the difference should give you the effect of the changes.
Which (finally!) brings me to my question: how should I choose the control group?
Suppose we are interested in how the load shape of a group of mid-size commercial buildings in a specific county was affected when those buildings add solar panels. One approach to choosing the control group would be to use “propensity score matching” or some similarly motivated approach. One of the problems is that I have very little information about the buildings, all I have is what is known to the utility: the rate plan they are on (there are a lot of different rate plans, especially for commercial buildings), their energy usage, possibly something about the physical size of the building. I could choose a control group of buildings that has the same mix of rate plans and approximate total energy usage and approximate physical size…but surely the companies that have bought solar panels will differ in important ways from those that don’t.
But also, this approach would discard an enormously useful type of information that I _do_ have, which is the load shape of the buildings. Surely I should try to choose control buildings that have load shapes (prior to installing solar panels) similar to the case buildings. In an ideal case, suppose there are two office buildings that have identical load shapes. In summer 2014 one of them adds solar panels. Surely the other one should go into the control group. So one tempting approach is to do something akin to medical case-matching. Perhaps, for each case building, I could choose N control buildings that have highly correlated loads (in the year before the solar panels were installed), and then create a “virtual” control building by taking a linear combination of the loads in those buildings. Something like that. So, ok, “something like that.” But what, exactly?
Can anyone point me to relevant publications, or tell me about past experience, or give me useful advice, about creating a control group for this kind of application?
Thanks in advance!
This post is by Phil Price, not Andrew.
tl;dr
http://economics.mit.edu/files/11859
“Building on an idea in Abadie and Gardeazabal (2003), this article investigates the application of synthetic control methods to comparative case studies”
Great, thank you for pointing this out!
The synthetic control type of strategy has been generalized to multiple treated units
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2584200
Excellent, thanks very much.
First reaction, you shouldn’t care much about individual buildings unless you believe the area under consideration does not reflect the larger pool well. It may be this is a specific industrial/office area unlike others. You could figure that out if you have data for the other buildings. You could even generate a variance factor, that your area is this much different up or down. It would also be interesting to know if an area, like an industrial park, has converted to solar, that is if the total area isn’t large enough so that kind of concern would be reasonably unimportant. I’d say more important would be factors like any existing trends toward changing rate plans or conservation methods because those would be a reasonable proxy for pressure of external factors. If your area is large enough, you could arbitrarily section it – literally by location or by random cuts or by specific factors like building size – to evaluate the effects of externality by comparing its effect, if material, across the areas. You could determine a factor, but being a derivative it would be sensitive to radical shifts in magnitude and sign. If you need to look at individual building shapes and you have sufficient total area, then you do the above and take shapes as a case and then cut up the case by actual size, by actual demand, etc. so you can calculate average usage both in trends and as a factor. But if you don’t have sufficient area, meaning data points and to some degree literal physical area, the question gets hard because you’ve internalized the externalities so you could have a perfectly accurate model for just your data but which is materially misleading when applied to other data.
You’re right that the utility is only interested in the aggregate of buildings (or at least that’s 90% of what they are interested in) but there are still advantages to modeling at the level of individual buildings, or at least subdividing them in various ways. For instance, the influence of outdoor air temperature on electric load is nonlinear, so if you have some buildings that are at 65F while others are at 75F (a common occurrence here in the SF Bay Area) you get a different electric load than if all of the buildings are at 70F. So the weather adjustment is best done at either small spatial aggregations or at the level of individual buildings.
That said, you are right that we are considering working with aggregations at small spatial scales rather than individual buildings.
see this recent paper
http://www.nber.org/papers/w22791
which also cites time-series approaches such as
https://research.google.com/pubs/pub41854.html
Terrific, thank you! Super helpful.
I do load forecasting and load research for a Midwest utility and this is a problem we are only beginning to tackle–we don’t have high adoption rates (yet) of electric vehicle chargers or solar panels to a degree where the impact to load is measureable, but I’m working on trying to run scenarios where the adoption rates of both increases over the course of the forecast period. On the residential side it isn’t as difficult; we can place interval-tracking meters on houses that currently have electric vehicles or solar and use those to compare to the load shape of those residential customers who do not have those technologies. Generally-speaking, the residential use behavior doesn’t vary substantially (as we are a summer-peaking utility, our annual system demand peak is almost always in the 5pm or 6pm hour of a particularly hot day), so with a sufficient sample of residences with interval meters you should have plenty of controls in your sample.
Commercial customers, on the other hand, are a completely different ball of wax: different types of businesses can have radically different load shapes. A 24-hour convenience store or data center will have a very different load factor and load shape compared to a local restaurant or insurance office.
In this scenario I would start specific and get more general–in a given geographic region, try to find similar business types on the same rate class with similar functions/hours with similar building square-footage (the footprint data is often available from your local county assessor and a local data consulting company might have aggregates of this sort of data that they keep on hand and can sell to you relatively cheaply), and then broaden the sample with commercial customers with similar load factors. Starting from just similar load shapes might introduce some noise as different commercial buildings might have things that could affect their load shape that are not related to each other. You can match up the square-footage data with customer management system data to sort out like types of businesses. It’s a little labor intensive that way, but you can use the tribal knowledge of the utility to streamline this a bit. And the load research group at the utility will probably have additional resources to access as the placement of their survey meters is often divided out into various strata to try and put like customers together.
The utility I’m doing this work for doesn’t even know which houses have electric vehicles, except for the houses that have switched to an electric-vehicle-specific rate plan. Our plan is to go ahead and look at those houses, but we will have to deduce (from the load data) when the vehicles are charged. Your ability to identify and meter those uses is enviable.
I’m a bit surprised that you find commercial customers more challenging than residential. In my experience commercial building load shapes are quite predictable (given historical interval meter data), whereas residential customers are very much not. If you’re willing to share some of your experience on this issue, please send me an email at pnprice at creekcats dot com, I’d rather avoid reinventing the wheel.
Ahh, this might actually be the advantage of working for a smaller utility as we tend to have a closer relationship with developments in our customer base (such as electric car customers). It also means the sophistication of our models do not need to be exceptionally high. Our load research, for example, is based on a randomly-selected sample of residential and non-demand commercial customers that we place interval meters on and infer from that sample what each customer class’s contribution to peak load is. In this sense, at least in my particular region, the residential customers are easier because their behaviors line up better–so they are easier in the *aggregate* as a customer class to model than commercial customers. On an individual level, barring a lot of switches in tenancy in a commercial facility, a commercial customer would be more predictable with themselves, but not necessarily in the aggregate where we are simply looking at the entire load shape of all customers combined, of which only a relative handful of individual non-demand customers has an interval recorder.
If you’re trying to capture the precise change in the load shape amidst the sea of noise in a large area, that is definitely challenging without interval data from those specific customers pre/post. With all that said, some of the more technically-minded people below appear to have a better idea for what to pursue if you do not in fact have interval data for solar customers *before* they became electric vehicle or solar customers.
I’m also guessing that the customers that are on electric vehicle rates aren’t being metered with interval recorders?
I don’t have an exact answer, but I can point you to a very well studied case from the 2015 eclipse that analyzed the losses of solar power over a large swath of Europe. https://www.entsoe.eu/Documents/Publications/ENTSO-E%20general%20publications/entsoe_spe_pp_solar_eclipse_2015_web.pdf
You might be able to extrapolate something useful from this report to help you identify criteria for a control group.
Good luck.
>>>One of the problems is that I have very little information about the buildings<<<
Is this a classical case of trying to replace good measurement / data by sophisticated modelling? Surely, if the decisions are so important for the utility we should be able to convince them to get better, richer data about the use cases of the buildings? Perhaps by offering incentives to commercial customers to volunteer more data about their particular usage patterns?
Surely, instead of just matching load curves it'd be easier to club together users based on a richer attribute set? e.g. I'd expect the business-type to be a strong predictor: load curve shapes of (say) strip malls as a group should be similar yet very different from chemicals-plants & yet very different from school-districts.
Trying to build a model agnostic of that info. sounds like intentionally handicapping oneself. It's like starting a clinical trial without passing out the usual participant screening questionnaire about pre-existing conditions & then post hoc trying to figure out who had (say) high BP by deconvoluting the collected data (when a simple question during induction would have sufficed).
We go to war with the data we have, not the data we want.
And if you’re asking: couldn’t I, a contractor paid by the hour to analyze a utility’s data to answer a particular question, convince them to embark on a huge program to convince the Public Utilities Commission to allow them to require businesses to provide more data and to pay to install hundreds of millions of dollars in meters, the answer is No.
“We go to war with the data we have, not the data we want.” I will put this on my future presentations ;) . Should I quote you as the author, Phil?
https://en.wikiquote.org/wiki/Donald_Rumsfeld
As Daniel pointed out, I took the form of the quote from Rumsfeld. But I changed “army” to “data” all by myself.
One thing to consider is using as much data as you can get without trying to match (and throwing away good data in the process) and then using a multilevel model with variance component that incorporates time of day and year. In other words, don’t throw out data in the name of making a 1:1 match (which will never be perfect), use the variation in the cases to help estimate the effects of variables. You have before and after not an experimental design, I think you are better off just treating it as an observational study with time varying variables.
I have quite a bit of experience with this kind of pre / post approach, in which you fit a model to the data prior to the intervention and use it to predict what would happen in the future without the intervention and do a subtraction. We are already going to apply that approach, which is in fact the conventional way this is done. But, as I mentioned in the post, there are some problems with this approach and I’m hoping case/control has something to add. At least I think it’s worth a try.
I think what Z mentions below makes the most sense in that case.
I think Elin is seconding my suggestion that you try a difference-in-difference analysis, which I’m not sure if you noticed I suggested at the end of my second comment (since you responded to everything else I said but not that).
Do a principal component analysis on the largest 4 or 5 fourier coefficients of each building’s load curve (the curve is close to periodic right?). Then take your N treatment buildings and build controls for each one based on some kind of distance in the principal component dimensions.
As with Z’s similar comment below, I’m already here with you…but I’m not sure what metric is best to use, among other questions.
One thing I might suggest is to divide all the Fourier components by the coefficient of the constant term. This then brings your Fourier components into dimensionless form and also normalizes to the size of the building. By the time you’ve done this, I’d be tempted to simply use euclidean distance. In fact, I’d be tempted at this point to predict the counterfactual load curves for my building by doing kernel-weighted averaging where the kernel weight is built from the euclidean distance of the normalized fourier principal components.
F_j(t) = sum(F_i(t) k(i,j))
where F_j is the counterfactual for your treated building, and F_i is the actual for *all* the untreated buildings, and k(i,j) is a weight related to how close the ith and jth buildings were pre-treatment in the principal components of the normalized fourier series. something like exp(-(distance(i,j)/sigma)^2) where distance(i,j) is the euclidean distance in the normalized principal components and sigma is a hyperparameter with an informative prior.
You could perhaps fit sigma by taking some randomly selected un-treated buildings and predicting their future curves from a similar technique.
In case I’m not being clear here, the principal component analysis is done on data from before the treatment, and then the counterfactual is estimated post-treatment by kernel weighted average of the post-treatment load shapes in the untreated buildings but using the kernel weights calculated from pre-treatment data. This is basically “weighted averaging the untreated buildings with larger weights for buildings that used to be more similar to the treated one”
The kernel is fit by randomly assigning “null treatments” to some of the control buildings. The counterfactual construction technique should predict “post treatment” well among randomly placebo-treated buildings, (ie. “treatment” assigned by random number generator). This is basically the same technique mentioned below: http://statmodeling.stat.columbia.edu/2016/12/15/can-time-series-information-used-choose-control-group/#comment-366075
If you’re going to apply a Fourier transform, won’t you need to window first? Those duck curves seem only approximately periodic.
I presume you have suitably high-frequency data so that aliasing will be minimal, right? I’ve seen cases where 15-minute data didn’t suffice for a particular device; I don’t know about the aggregate across a building.
@Daniel: I saw that I replied to your second Fourier transform comment, but you already mentioned periodicity in your first. If Phil expands the extent of a load curve to include multiple days, then he can get better resolution on the Fourier components, right, and he can window with a bit more impunity (there will be more data in the middle that’s not affected by the windowing).
“Inferring causal impact using Bayesian structural time-series models” by Kay H. Brodersen, Fabian Gallusser, Jim Koehler, Nicolas Remy, Steven L. Scott from Google, available at https://research.google.com/pubs/pub41854.html. Also, pretty pictures from the available R package: https://google.github.io/CausalImpact/CausalImpact.html.
The other thing is that home battery technology is getting a whole lot better so that might take some of the load off at peak time.
I don’t get this part: If battery technology is getting good enough for homes to do load balancing why aren’t the utilities the first to install massive battery banks?
If it makes economic sense to install a battery bank in your garage for off peak consumption wouldn’t it make greater sense for the utility to internalize the gains? And an economy of scale?
What gives?
If the battery is good enough to allow many many charge/discharge cycles, then it makes sense to double-use batteries for powering cars and for smoothing power even if by itself the smoothing power issue isn’t cost effective.
Isn’t battery life charge-discharge-cycle related? If you double use, don’t you just end up making even the cars *less* cost effective?
Battery technology is not yet good enough for homes to do rate arbitrage.
Many companies are on rate plans that charge “demand charges” which are essentially a penalty based on the highest load for the entire month, even if it was reached for only 15 minutes. Some industrial companies have extremely peaky loads and can reduce their demand charges by installing huge battery banks. They do this. But to substantially reduce the load over a long, gradual peak and then recharge again at night, the volume under the curve — the capacity of the battery that you need — is very high, which makes it a huge capital investment. It doesn’t make sense except in extreme cases. This could change in the future.
So the real take-home conclusion for me is that the rate plans we have today are irrational.
The peak charges are too high and hence we are incentivizing the ineffective use of home-battery packs for peak shaving. It’s a market distortion really.
The utilities are penalizing too much for the peaks. If the penalty was in line with the actual costs of providing stand by peak capacity it’d be axiomatically viable for the utilities to install battery-power-banks already.
http://www.snopud.com/PowerSupply/energystorage/projects.ashx?p=2800
Note that what you’re describing is not a case-control study. Case-control studies sample units that experience an outcome (the cases) and units that do not (the controls). This is a confusing use of the word ‘control’ because in other contexts ‘control’ means ‘no treatment’ as opposed to ‘no outcome’, but nevertheless this is the meaning of ‘control’ in a case-control study. You’re talking about just plain matching.
I don’t quite understand this (which is not to say I disagree with it). There are buildings that installed solar panels and buildings that do not. I’m calling the former the “cases” and the latter the “controls.” To me, this seems similar to, say, quantifying the long-term health effects of malaria by comparing people who got it (the cases) with people who didn’t (the controls).
As for a matching approach, yes, there are many metrics for the distance between two time series. Which one is most appropriate here, is part of my question?
You are using the term control in the sense where it contrasts with “treatment” i.e. that the controls did not get the treatment. But that is not what control means in a case control study. In a case control study you sample on the dependent variable, you get people that died and people who didn’t die and then compare whether they took Vitamin B. It’s basically sampling on the dependent variable. You are definitely not interested in a case control study.
You have an interrupted time series (or as they say in social work an AB single system design) with multiple time series.
So the analogy would be what, sample on whether you install solar panels and then look to see if the CEO of the company is vegan?
https://en.wikipedia.org/wiki/Case-control_study
So, yes ;-)
elin:
Phil might have a choice here, as a first sketch the case-non-case (case-control) study would identify buildings that adopted solar panels and then identify match non-cases while the cohort study would collect information on a sample of buildings and identify which had adopted solar panels and which haven’t and try to do a balanced comparison on the basis of pre-adoption data.
This sort of decision might be more important than the details of the analyses given the study decided on.
If he is in for the full or long war he might wish to (re)read stuff by Rubin (e.g. Causal Inference in Statistics, Social, and Biomedical Sciences), Rosenbaum (Design of Observational Studies) and even Pearl if the mechanisms of adoption and effects of adoption are well understood.
There seem to be a lot of good suggestions here, but they are fairly specific.
If its a one off battle – that will likely have to do.
That’s clever. You could also do a Heckman selection bias kind of model there.
If you pursue the matching approach, it seems like what you’re after is a metric for the distance between two time series. There are many such metrics which you can easily google. As you said, though, matching on past load curve is probably not sufficient to control for all confounding. You might want to try a difference-in-difference analysis to hopefully get rid of some of the residual confounding.
As already pointed out by others, I think difference in differences/synthetic control is a perfect match for your problem.
From what I’ve seen of that literature, the distance metric of the time series or the load isn’t actually that important. With many units of analysis, it is very easy to choose a combination of non-treated (no solar panel) units that will give a load curve that matches the average load curve of the treated units (solar panel) pretty much exactly, pre-treatment.
Instead, the most serious problem is that there is no guarantee that this match of loads between treatment and control will continue for the non-matched periods in time afterwards, which is exactly what you need to closely approximate the loads of solar panel units in the counterfactual scenario where they have no solar panels.
In the synthetic control literature, I believe they restrict how you can combine units to construct the synthetic control to convex combinations in order to get some regularisation and make getting a match a bit harder, but it’s questionable whether that’s enough. Instead, it’s probably best if in addition, you select control units based on substantive reasons why their loads should be similar to he treated, if there are any, instead of just based on the observed similarity of the load curves before the treatment.
The other thing commonly suggested in the literature is that you carry out placebo tests: Synthetic controls should continue to match treated units beyond the period over which they match it by construction, and you can check that for “placebo” treatments: points in time when nothing changed. You construct the synthetic controls using a period preceding those points and then compare their load with the treatment units going forward in time. The loads should diverge only slowly if the approach is to have any hope.
This gives you a sense of how good the approximation of the counterfactual is likely to be.
Forgive me, I have not read all the comments, because #obvious reasons. But in identifying ‘like’ buildings, have you seen:
https://www.jstatsoft.org/article/view/v067i05/v067i05.pdf
which is in this R package
https://cran.r-project.org/web/packages/pdc/pdc.pdf
>”Which (finally!) brings me to my question: how should I choose the control group? Suppose we are interested in how the load shape of a group of mid-size commercial buildings in a specific county was affected when those buildings add solar panels.”
I don’t imagine knowing the effect of solar panels while keeping everything else exactly the same has much real world relevance, it just isn’t going to happen. But maybe I am wrong. Say that Omniscient Jones told you the exact effect, there is no uncertainty about the modelling, sampling bias, etc. How would you use that info?
My point is, I think you should reconsider why it is so important to isolate the “effect” of solar panels, which will no doubt be correlated with many other factors. What is the end goal here, the actionable info? If it is prediction of the future load shape (which I suspect), just make a prediction that takes into account solar panels + whatever else.
This is a problem for the utility, not for me, but they are certainly aware of this problem and are grappling with it.
They have groups that attempt to forecast the future when it comes to electricity demand, and one of several approaches is by looking at individual technologies: what do they think will happen with electric vehicles, photovoltaics, etc.? As they know very well, the future will depend on all sorts of things, including the state of the economy, and the rate of improvements in the technologies, and the types of subsidies available to purchasers, and on and on. They do their best to predict these things. But how can they even tell if they are doing a good job? If they think that the typical electric vehicle owner five years from now will drive 30 miles per day and will plug in around 5:30 PM and will take 11.6 kWh for a full charge, how do they check that? They need some way of knowing what is actually happening.
Sorry, posted prematurely.
They need some way of knowing what is actually happening, so in five years they can see what is actually happening and compare that to what they thought would happen.
Also, if they know what happened in each of the past five years, perhaps that can help them extrapolate into the future.
Predicting what the future will look like is always hard. It’s even harder if you don’t know what the past and present look like either.
+1
Excellent point. I think we spend too much time on the “how to model” question & not enough on the “What do we need to model”.