Here’s a cool interactive demo of linear regression where you can grab the data points, move them around, and see the fitted regression line changing. There are various such apps around, but this one is particularly clean:
(I’d like to credit the creator but I can’t find any attribution at the link, except that it’s from the Université de Namur, Site web Pratique des biostatistiques.)
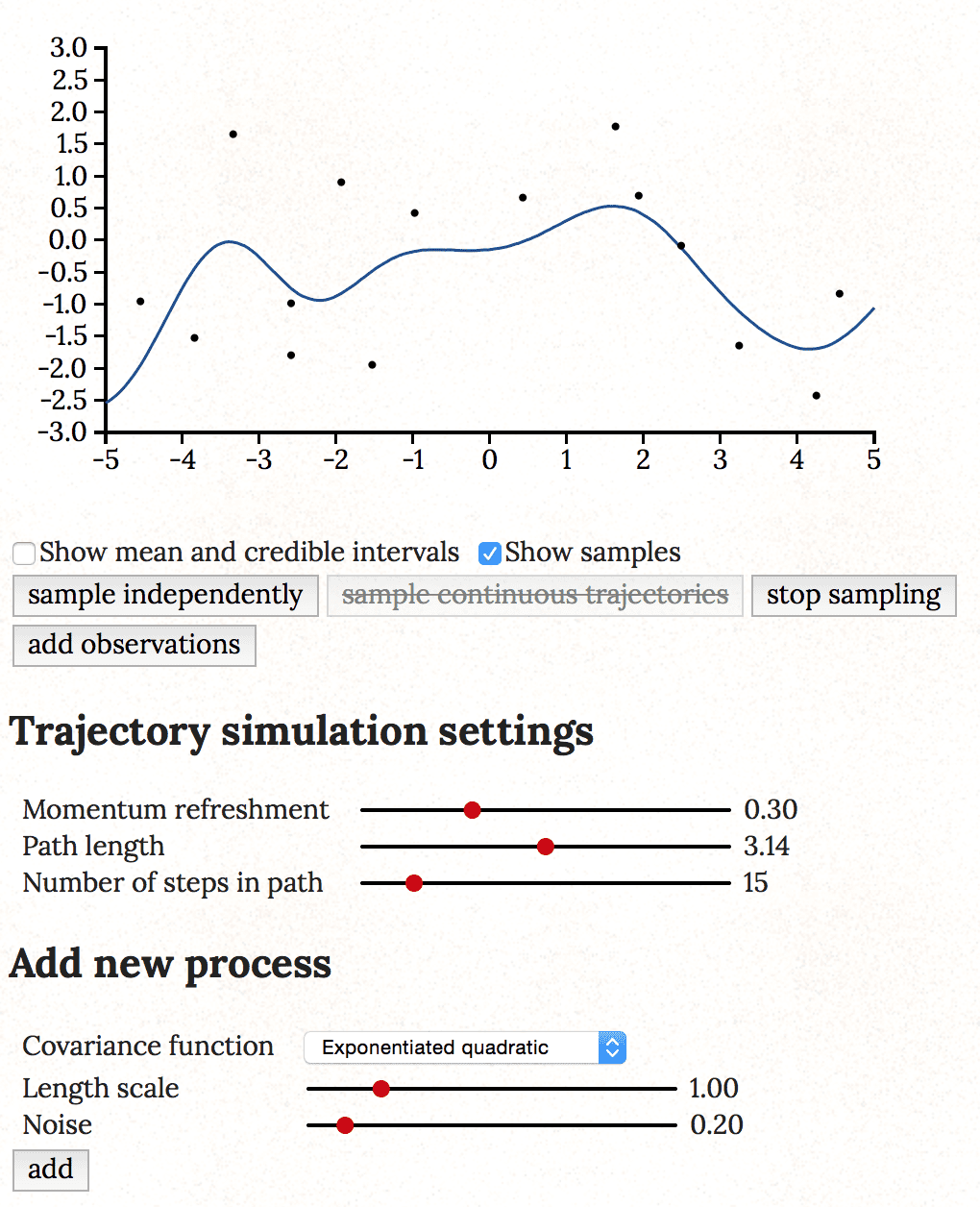
And here’s something similar for Gaussian process regression, where you can add data points, play with the hyperparameters, and then see the inference for the curve. It’s by Tomi Peltola:
Good stuff.
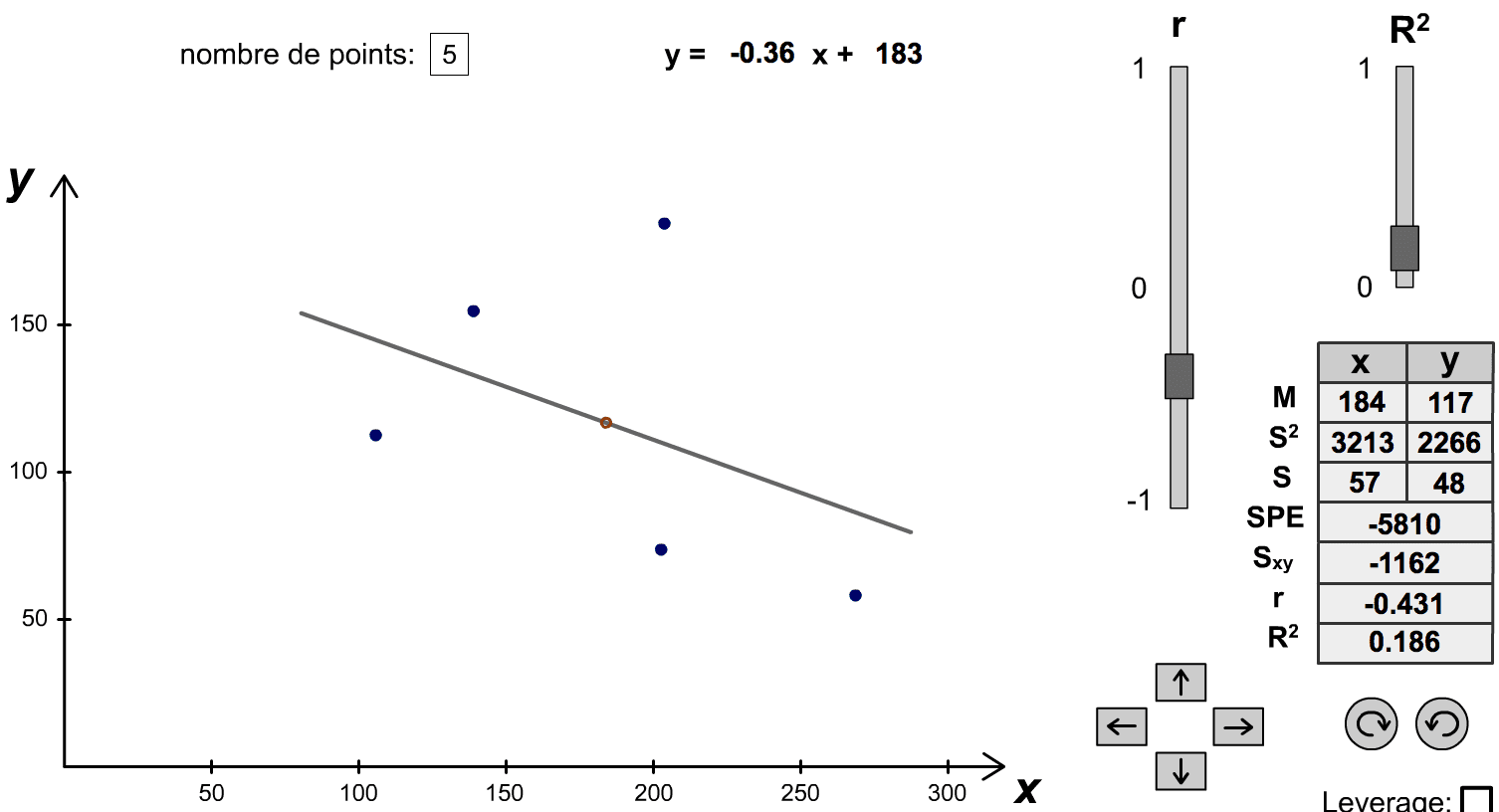
I’ve been working on something similar with regression diagnostic plots:
http://www.refsmmat.com/regression/regression.html
It’s rather incomplete at the moment, but it works. You can drag data points around and see what happens to the diagnostics (residuals, standardized residuals, Cook’s distances, etc.). I particularly like that you can hover your mouse over a data point and highlight where it is in the diagnostics. I’m planning to eventually build a set of examples with different datasets and write some explanatory text.
Prof.Gelman, what’s a good R GP package you recommend? I know BACCO package does it, http://cran.r-project.org/web/packages/BACCO/index.html, but it’s complicated to setup.
Ooh ooh, I know this one! RStan.
Corey, I actually ran RStan, it’s not fast and computational expensive.
Try gpstuff.
I didn’t understand what the second demo was doing….
It’s sampling from the posterior distribution of a Gaussian process, either by drawing independent samples from the posterior or by simulating continuous trajectories using Hamiltonian Monte Carlo (HMC).
Think of the curve as a set of discrete points ordered along the x-axis (which it really is), where the y-axis value of the points have a joint multivariate Gaussian prior N(0, K), where K is the covariance matrix that is evaluated using some covariance function (covariance between two points depend on their distance on the x-axis). The observations that you can add are assumed to have a Gaussian likelihood associated with them. Conditioning on the observations will then give a multivariate Gaussian posterior distribution N(m, S), where m is the mean and S is the covariance matrix.
Now, independent samples are, well, just independent samples from this posterior distribution. The continuous trajectories are sampled using Hamiltonian Monte Carlo, where, in the case of a Gaussian distribution, the Hamilton’s equations can be solved in closed form and do not need numerical integration or Metropolis acceptance step. Usually, and for example in Stan, you are only given the samples at the end of a single trajectory (after simulating the Hamiltonian dynamics for some “integration time” or “path length” after which the momentum is re-sampled), but the linked visualization shows also the steps along the trajectory (the number of intermediate values shown is the “number of steps in path”). To give more continuous feeling to the sampling at the end of single trajectories, the visualization also refreshes the momentum variables in HMC only partially (depending on the “momentum refreshment” setting).
Thank you!
Pingback: Distilled News | Data Analytics & R
Here’s one more: http://lukaszkujawa.github.io/gradient-descent.html
The authors of the app can be found at
http://webapps.unamur.be/biostats/biostat/communs/auteurs.html