David Hogg writes:
I thought this was either interesting or bunk—using online games to infer how various kinds of cognitive intelligence vary with age. I thought it might be interesting to you on a number of levels. For one: Are there really categories of intelligence and can these map onto online games? For another: How do you make conclusions about the population as a whole from the population that participates in online games. They find age effects, but I bet there are age effects in the participation rates…
Hogg is referring to a press release by Anne Trafton describing an article by Joshua Hartshorne and Laura Germine, “When Does Cognitive Functioning Peak? The Asynchronous Rise and Fall of Different Cognitive Abilities Across the Life Span.” From the press release:
Scientists have long known that our ability to think quickly and recall information, also known as fluid intelligence, peaks around age 20 and then begins a slow decline. However, more recent findings, including a new study from neuroscientists at MIT and Massachusetts General Hospital (MGH), suggest that the real picture is much more complex.
The study, which appears in the journal Psychological Science [uh oh — ed.], finds that different components of fluid intelligence peak at different ages, some as late as age 40. . . .
I’ve heard that blogging peaks at the age of 50, actually.
Seriously, though, their general approach seems reasonable. I’d like to see some raw data, though. Also, for some of the tasks, the idea of “peak performance” seems to miss the point. Consider this figure from the Hartshorne and Germine paper:
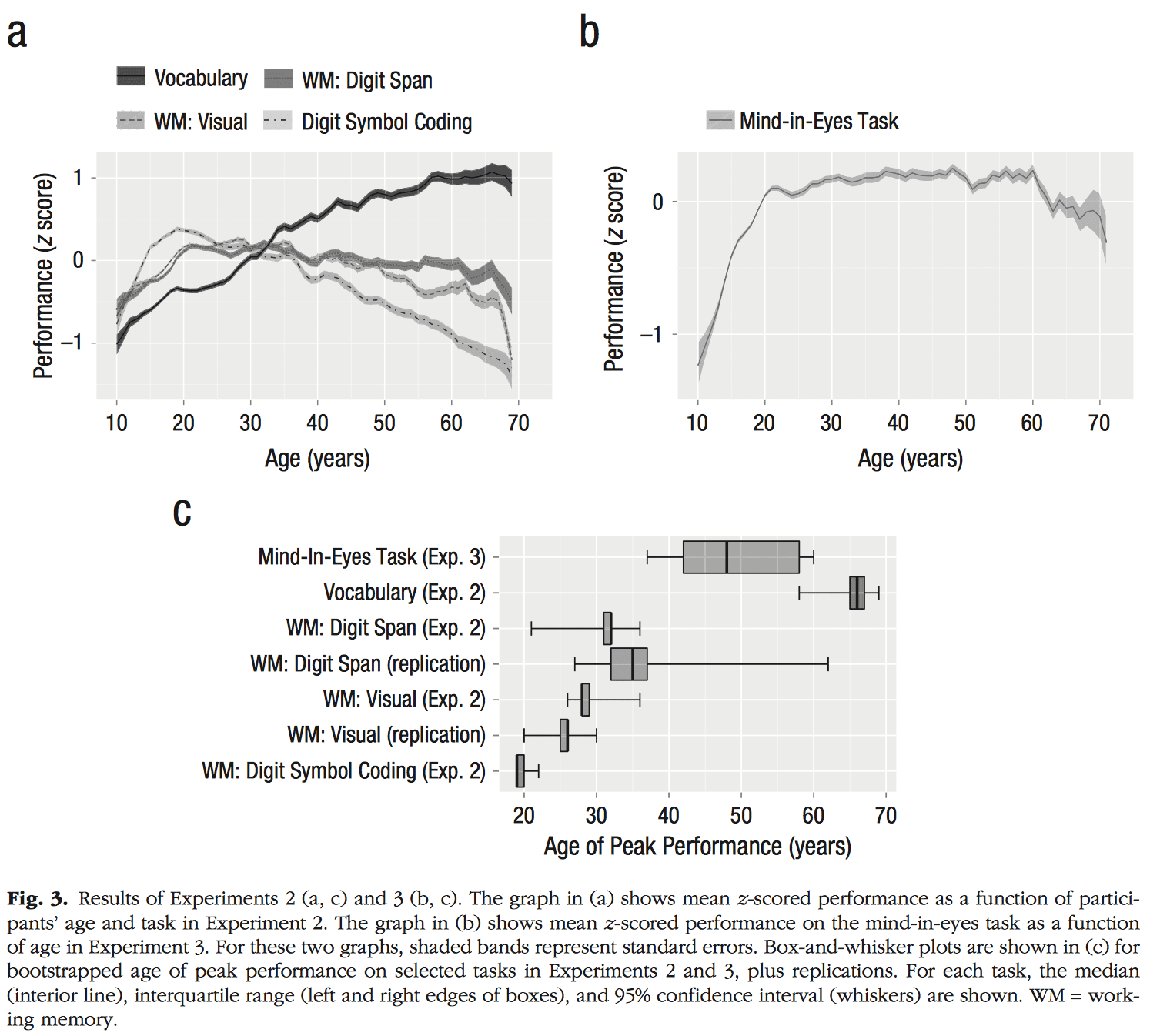
First, it’s hard for me to believe this is showing raw data: The lines in figure a and b look too smooth. Second, in a graph such as figure b, there’s no peak to find. This seems like a limitation of the statistical approach: Before seeing the data, it would seem to make sense to look for a peak, but not so much after.
I also wonder whether many of these curves could be usefully categorized as the sum of two curves: a gradually increasing curve representing “experience” and a sharply decreasing curve representing “performance.”
There’s also the difficulty of disentangling age, period, cohort effects. The authors do discuss this in their paper but I don’t think they resolve it.
In summary, I find this paper to be interesting. A few more like this, and Psychological Science might get a good reputation! I think more could be done here by modeling the data a bit. Lots to look into here.
Thanks for taking the time to take a look at our paper, Andrew! We actually have published our data on the Open Science Framework and would very much like people to play around with it. The more eyes the better: https://osf.io/4xp3g/
As for representativeness in the older age groups, we agree it’s an open question – in our paper, we were able to compare our vocabulary data with the vocabulary data from the General Social Survey and find broadly similar results in terms of age-related differences. It’s also, however, a moving target as internet penetrance is still increasing and older folks are becoming more and more computer / web savvy.
Laura Germine
I’m surprised that Andrew didn’t mention Wei et al.’s Xbox paper (predicting voting for the population from Xbox survey respondents) to answer David’s question about how to adjust population predictions using poststratification.
I’ve heard Hartshorne talk and have taken some of the online tests. There are slides of various plots of the data and they show much greater variance in older over younger ages in each area tested. Some of the decline in older ages seems intuitively to be more a function of overall decline, meaning health in that part of the tested population, but I don’t know all their data sources and there isn’t anything about health in the online testing.
That Vocabulary Task does not seem to have a peak at all from eyeballing the graph. Yet the other graph ascribes it a ~65 year peak ability.
I’m not sure why.
Peaks were defined relative to the data observed. So the peak *in the dataset* averaged around 65. What would have happened if we had more older subjects, I can’t tell you.
Perhaps I’m missing some subtle issue, but from the plot of the Vocabulary Task data “No Peak Found” or “Ability continues improving with age” or at least “Ability increases and plateaus out at 65” seemed like the conclusion I’d go with.
I sure didn’t notice any significant decline. And when you say “peak” I expect that.
I don’t think “peak” requires a significant decline. But in any case you are looking at just one of the graphs from one experiment. It does not show a decline, but the age range is relatively restricted. The others show it more clearly.
I think figure C could be improved by adding points indicating the mean/median individual peak estimates flanked with 95% hdis (or other interval that works best). The average peak could be highly misleading. For example, one subgroup “peaks” at t=10 and decays while the other monotonically increases until t=70. There could actually be no observable peak at all, yet result in those average curves.
Averaging artifacts have plagued learning curves for quite some time. I have read papers going back to the 1930s complaining about this (can’t find the reference at the moment), but for example:
http://www.ncbi.nlm.nih.gov/pubmed/15331782
Actually, after glancing at the data I see it is not longitudinal (in retrospect I should have guessed that). So this is more of an understandable, but major limitation. I would be extremely wary of drawing conclusions about age of peak performance from this.
I’m not sure what you are asking for. Figure C shows the median, interquartile range, and 95% confidence interval. What would you want in addition?
I did not realize you lacked individual-level (one for each person) performance curves until I wrote the last paragraph. I figured I would leave it because the (non-longitudinal) data you have is even more difficult to interpret.
If you had the individual curves, I was asking for an overlying stripchart with the points corresponding to the estimates of “age of peak performance” for each person. Figure C only shows the “group-level” estimates. The purpose would be to indicate whether the distribution was multimodal. Versions of figures A/B that show the shape of the distribution for various age groups would be the best available substitute.
If there are subgroups, the “peak” may only exist in the averaged data. The peak may not correspond to anything occurring at the individual level. Attempts to explain it using cognitive processes would be a big waste of time.
As an example, say there are two individuals y1/y2. Then the average appears peaked (dotted black curve) while neither individual (blue/red curves) has a peak:
x=10:70
y1=100*(1-1/exp(.1*x))
y2=100*(1/exp(.02*x))
avg=rowMeans(cbind(y1,y2))
http://s23.postimg.org/ave87x7fd/perform.png
Anoneuoid/Josh,
So OK suppose that one of the big factors impacting the “peak” of the skills-age profile is education (seems reasonable enough to me). Then, supposing your Y1/Y2 types from below are determined by education, separately plotting the age-profiles by education would reveal the effect in the mean without need for individual-level data.
I guess my point is that if you have some knowledge of the things that determine what “type” of life-trajectory an individual is on, you can get much of what you want with cross-sectional data and don’t need a panel. And if it is all unobserved/unobservable, then maybe the average isn’t super informative, but neither is the panel data (it just shows us there are no clear patterns in human development over age – I suspect this is probably untrue and that there are some real patterns and these patterns vary by both observables and unobservables).
If we have repeated cross-sections, then I think some of the cohort-period-age problems can be taken care of too. I actually think that sometimes repeated cross-sections by us more than panel data in this regard (unless you have a panel that is repeatedly enrolling new people over time).
>”So OK suppose that one of the big factors impacting the “peak” of the skills-age profile is education (seems reasonable enough to me). Then, supposing your Y1/Y2 types from below are determined by education, separately plotting the age-profiles by education would reveal the effect in the mean without need for individual-level data.”
But we can also come up with sets of individual curves with peaks that appear monotonic when averaged, so the peaks may exist after all (but not at the age indicated by the overall average). Our experience with learning curves shows it really is dangerous to attempt explaining average curves rather than individual-level. Inspecting that literature is really the best way to see why this is so. From Gallistel et al. (2004) linked above:
“The potentially misleading nature of the group learning curve becomes serious when modelers try to make their model of acquisition process approximate the group curve, rather than the curve typical of the individual subject. For example, Kakade and Dayan (9) set as a criterion for a successful model of conditioning its ability to capture the prolonged increase in performance seen in Fig. 1 (which they also take from figure 2 in ref. 10, p. 227). We now show that in most subjects, in most paradigms, the transition from a low level of responding to an asymptotic level is abrupt.”
I do think these peaks may exist and this is all very interesting. Actually, right now there is a plot of a “machine learning curve” on my screen. If the learning rate is set too high, the performance on the training data monotonically increases but there is a peak on the test data. The reason is that at some point the algorithm begins over-fitting to the training data, reducing the ability to generalize.
A similar phenomenon may happen as people age and become more specialized. There would be a trade-off between the speed at which specialized skills can be learned and ability to generalize the skills to unfamiliar circumstances.
Anoneuoid,
That paper is really interesting. Thanks for pointing me to it (I skipped over the first time). I think we totally agree on the ease with which learning curves (or age-profiles in general) can be misleading in the mean and that tracing out individual changes over age has a lot of benefits. But I also think two other things:
1 – In some cases, we actually know something about the world that makes the mean age-profile interesting. For instance, human physical growth (height) – it increases monotonically, and I think that using the mean would allow you to estimate an interesting parameter like the average rate of growth at various ages (or the effect of some input X at age A on outcome Y at any age A+T). Sure, there would be individual-level differences in the speed of growth, but I think the aggregate would be still informative in a situation like that. Maybe sector-specific wage-profiles too, which are not grounded in biological necessity but still sort of bounded by the way the labor markets function.
2 – I think that taking the outcome-age profile as an object of interest in quantitative investigations of human health, learning, earnings, or other outcomes is totally under-explored in the literature in economics and has been (in my limited experience) surprisingly crudely done in the psychology and other literatures. Sure, you might see age-group specific effects, but the idea of trying to understand how humans grow and age is generally lost in the desire to estimate mean group effects and apply simple p-values to make decision rules. I’d love to see more methodological work on assessing the causal impacts of programs/policies/inputs on the trajectory of human outcomes over the life course. So I liked this work precisely because it seemed to be pushing in that direction – even if I think comparing age profiles is more informative than simply describing them in the mean (you know, because causal inference comes from comparing people exposed to different things).
Just a heads-up that the post http://statmodeling.stat.columbia.edu/2015/10/05/pmxstan-an-r-package-to-facilitate-bayesian-pkpd-modeling-with-stan/ (and any page or feed it appears in) really upsets Chrome.
I’m using Ver 45.0.2454.94
Doire
+1
It just crashes my Chrome everytime.
“Version 45.0.2454.101 m” on Windows 7
The image was too big. I fixed the post.
“I’ve heard that blogging peaks at the age of 50, actually.”
I think for me, it peaked at age 70. ;~)
I think this fall on the interesting side. There are limitations to the data, but it seems like it could compliment other work. For example, it is quite well known that vocabulary peaks at quite a high age (there used to be quite a lot of work on ‘crystallised intelligence’ looking at expertise and knowledge in older people and this was a consistent finding).