tl;dr: Negative expected return.
Long version:
I received the following email the other day from Tom Daula:
Interesting applied project for your students, or as a warning for decisions under uncertainty / statistical significance. Real money on the line so the length of time and number of entries required to get a winner may be an interesting dataset after this is all done.
I replied that I think the question, “the increase in global temperatures is probably not due to random natural variation,” is fundamentally unanswerable.
Daula wrote back:
True, but the objective function is well specified: “correctly identifies at least 900 series: which series were generated by a trendless process and which were generated by a trending process.”
The subject matter that motivated the problem is largely irrelevant. Although that could be a blog post on how this is the wrong way to state the signal to noise problem.
And I replied:
From the standpoint of climate science I don’t think this is so interesting because, from what I’ve seen, the evidence for climate change does not come from any single series but rather from many sources. But I agree that it would be an excellent teaching example.
And so I was going to post on it but then I thought I’d take a careful look. $100,000 on the line! Sure, Damon Runyon, Jack of Spades, etc. But still, let’s take a look. The webpage is from someone named Douglas J. Keenan and it starts like this:
It has often been claimed that alarm about global warming is supported by observational evidence. I have argued that there is no observational evidence for global-warming alarm: rather, all claims of such evidence rely on invalid statistical analyses.
Some people, though, have asserted that the statistical analyses are valid. Those people assert, in particular, that they can determine, via statistical analysis, whether global temperatures have been increasing more than would be reasonably expected by random natural variation. Those people do not present any counter to my argument, but they make their assertions anyway.
In response to that, I am sponsoring a contest: the prize is $100 000. In essence, the prize will be awarded to anyone who can demonstrate, via statistical analysis, that the increase in global temperatures is probably not due to random natural variation.
That’s the famous $100,000. And now for the contest:
The file Series1000.txt contains 1000 time series. Each series has length 135: the same as that of the most commonly studied series of global temperatures (which span 1880–2014). The 1000 series were generated as follows. First, 1000 random series were obtained (via a trendless statistical model fit for global temperatures). Then, some randomly-selected series had a trend added to them. Some trends were positive; the others were negative. Each individual trend was 1°C/century (in magnitude)—which is greater than the trend claimed for global temperatures.
A prize of $100 000 (one hundred thousand U.S. dollars) will be awarded to the first person who submits an entry that correctly identifies at least 900 series: which series were generated by a trendless process and which were generated by a trending process.
But also this:
Each entry must be accompanied by a payment of $10.
OK, now it’s time to get to work.
I’ll start by downloading and graphing the data:
series <- matrix(scan("Series1000.txt"), nrow=1000, ncol=135, byrow=TRUE)
T <- 135
N <- 1000
pdf("series_1.pdf", height=5, width=6)
par(mar=c(3,3,2,0), tck=-.01, mgp=c(1.5,.5,0))
plot(c(1,T), range(series), bty="l", type="n", xlab="Time", ylab="series")
for (n in 1:N){
lines(1:T, series[n,], lwd=.5)
}
dev.off()
And here's what we see:
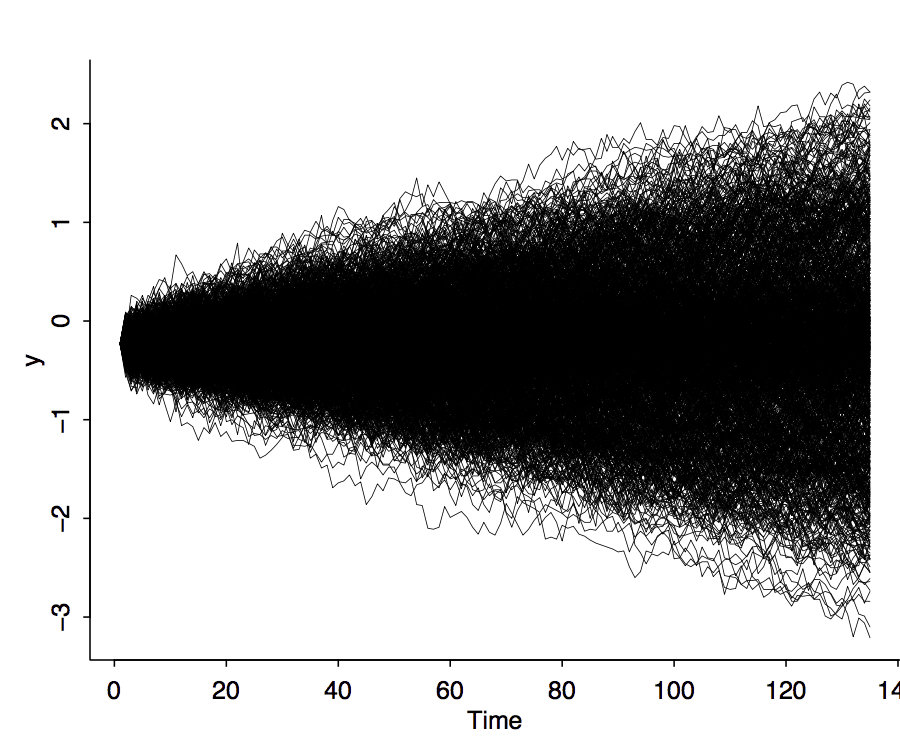
Aha! The lines are fanning out from a common starting point. I think I'll fit a regression to each line and then summarize each line by its average slope:
library("arm")
slope <- rep(NA, N)
se <- rep(NA, N)
for (n in 1:N){
data <- series[n,]
time <- 1:T
fit <- lm(data ~ time)
slope[n] <- 100*coef(fit)[2]
se[n] <- 100*se.coef(fit)[2]
}
I multiplied the slopes (and standard errors) by 100 to put them on a per-century scale to match the above instructions.
Now I'll plot the estimated slopes and their standard errors:
pdf("series_2.pdf", height=5, width=6)
par(mar=c(3,3,2,0), tck=-.01, mgp=c(1.5,.5,0))
plot(slope, se, bty="l", xlab="Slope", ylab="SE", pch=20, cex=.5)
dev.off()

OK, not much information in the se's. How about a histogram of the estimated slopes?
pdf("series_3.pdf", height=5, width=6)
par(mar=c(3,3,2,0), tck=-.01, mgp=c(1.5,.5,0))
hist(slope, xlab="Slope", breaks=seq(floor(10*min(slope)), ceiling(10*max(slope)))/10)
dev.off()
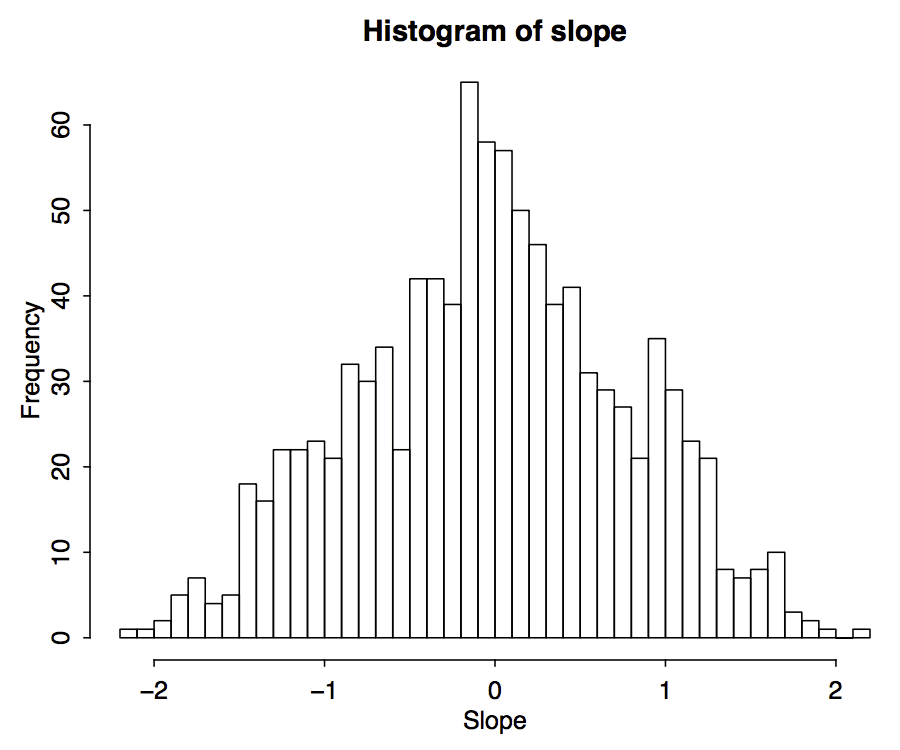
Based on the problem description, I'd expect to see distributions centered at 0, -1, and 1. It looks like this might be the case.
So let's fit a mixture model. That's easy.
Stan code in file mixture.stan:
data {
int K;
int N;
real y[N];
real mu[K];
}
parameters {
simplex[K] theta;
real sigma;
}
model {
real ps[K];
sigma ~ cauchy(0,2.5);
mu ~ normal(0,10);
for (n in 1:N) {
for (k in 1:K) {
ps[k] <- log(theta[k]) + normal_log(y[n], mu[k], sigma);
}
increment_log_prob(log_sum_exp(ps));
}
}
R code to run and display the Stan model:
y <- slope
K <- 3
mu <- c(0,-1,1)
mix <- stan("mixture.stan")
print(mix)
Check it out how you can just run Stan by giving the file name! The data are taken by default from the R workspace, and it does 2000 iterations and 4 chains if you don't specify otherwise. As a user, I find it convenient to have such a clean function call.
And here's the fit:
Inference for Stan model: mixture.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta[1] 0.54 0 0.02 0.49 0.52 0.54 0.55 0.58 2449 1
theta[2] 0.24 0 0.02 0.21 0.23 0.24 0.25 0.27 2537 1
theta[3] 0.22 0 0.02 0.19 0.21 0.22 0.23 0.26 2444 1
sigma 0.40 0 0.02 0.37 0.39 0.40 0.42 0.45 2078 1
Convergence is fine, the weights of the three mixture components are approx .5, .25, .25. In fact, given that the problem was made up, I'm guessing the weights of the underlying data-generation process are .5, .25, .25. The standard deviation of the slopes within each component is .4, or close to it. I could also try fitting a model where the sd's differ, but I won't, partly because Keenan just described the change as adding a trend, and partly because the above histogram doesn't seem to show any varying of the sd's.
OK, now we're getting somewhere. To make predictions, we need to know, for each series, the probability of it being in each of the three components. I'll compute these probabilities by adding a generated quantities block to the Stan program:
generated quantities {
matrix[N,K] p;
for (n in 1:N){
vector[K] p_raw;
for (k in 1:K){
p_raw[k] <- theta[k]*exp(normal_log(y[n], mu[k], sigma));
}
for (k in 1:K){
p[n,k] <- p_raw[k]/sum(p_raw);
}
}
}
I have a feeling this could be done with less overt looping, but it gets the job done.
I then re-fit the model (unfortunately, in Stan you have to re-run the model if you make changes to the generated quantities; it doesn't know how to just take the existing simulations and feed them in) and write some R to extract the p's and average them over the posterior simulations:
mix <- stan("mixture.stan")
print(mix, pars=c("theta", "sigma"))
prob_sims <- extract(mix, "p")$p
prob <- array(NA, c(N,K))
for (n in 1:N){
for (k in 1:K){
prob[n,k] <- mean(prob_sims[,n,k])
}
}
I now have a matrix of probabilities. Let's take a look:
> pfround(prob[1:10,], 2)
[,1] [,2] [,3]
[1,] 0.09 0.00 0.91
[2,] 0.40 0.60 0.00
[3,] 0.93 0.01 0.06
[4,] 0.83 0.17 0.00
[5,] 0.82 0.18 0.00
[6,] 0.95 0.01 0.05
[7,] 0.74 0.00 0.26
[8,] 0.86 0.14 0.00
[9,] 0.11 0.00 0.89
[10,] 0.87 0.00 0.13
So, the first series is probably drawn from the sloping-upward model; the second might be from the null model or it might be from the sloping-downward model; the third, fourth, fifth, sixth, seventh, and eighth are probably from the null model; the ninth is probably from the sloping-upward model; and so forth.
I'll now program this: for each of the 1000 series in the dataset, I'll pick which of the three mixture components has the highest probability. I'll save the probability and also which component is being picked:
max_prob <- apply(prob, 1, max) choice <- apply(prob, 1, which.max)
And now we can sum this over the 1000 series. I'll compute the number of series assigned to each of the three choices, the expected number of correct guesses (based on the posterior distribution we have here), and the standard deviation of the number of correct guesses (based on the reasonable-I-think assumption of independence of the 1000 series conditional on the model). And then I'll print all these numbers.
expected_correct <- sum(max_prob) sd_correct <- sqrt(sum(max_prob*(1-max_prob))) print(table(choice)) pfround(c(expected_correct, sd_correct), 1)
The result:
1 2 3 559 232 209 [1] 854.1 10.3
The guesses are not quite in proportion 500, 250, 250. There seem to be too many guesses of zero slope and not enough of positive and negative slopes. But that makes sense given the decision problem: we want to maximize the number of correct guesses so we end up disproportionately guessing the most common category. That's fine, it's how it will be.
The interesting part is the expected number of correct guesses: 854.1. Not quite the 900 that's needed to win! The standard error of the number of correct guesses is 10.3, so 900 is over 5 standard errors away from our expected number correct. That's bad news!
How bad is it?
> pnorm(expected_correct, 900, sd_correct) [1] 4.331203e-06
Ummmm . . .
> 1/pnorm(expected_correct, 900, sd_correct) [1] 230882.7
That's a 1-in-230,000 chance of winning the big prize!
Hmmm, we only have to get at least 900. So we can do the continuity correction:
> 1/pnorm(expected_correct, 899.5, sd_correct) [1] 184458.4
Nope, still no good. For the bet to be worth it, even in the crudest sense of expected monetary value, the probability of winning would have to be at least 1 in 10,000. And that's all conditional on the designer of the study doing everything exactly as he said, and not playing with multiple seeds for the random number generator, etc. After all, he could well have first chosen a seed and generated the series, then performed something like the above analysis and checked that the most natural estimate gave only 850 correct or so, and in the very unlikely event that the natural estimate gave 900 or close to it, just re-running with a new seed. I have no reason to think that Keenan did anything like that; my point here is only that, even if he did his simulation in a completely clean way, our odds of winning are about 1 in 200,000---about 1/20th what we'd need for this to be a fair game.
Can we do any better? We might be able to get slightly more precision by making the guess that the true values for the mixture weights are the round numbers .5, .25, .25, and that the true value for the sd parameter is .4.
With all these parameters known, I can just compute the membership probabilities directly in R, no need to fit any model. So here goes:
theta_true <- c(.5, .25, .25)
sigma_true <- .4
prob_simple <- array(NA, c(N,K))
for (n in 1:N){
prob_0 <- theta_true*dnorm(y[n], mu, sigma_true)
prob_simple[n,] <- prob_0/sum(prob_0)
}
Just to check, I'll plot the estimated probabilities from before and the new estimated probabilities, for the first 10 lines of data:
> pfround(cbind(prob, prob_simple)[1:10,], 2)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.09 0.00 0.91 0.06 0.00 0.94
[2,] 0.40 0.60 0.00 0.37 0.63 0.00
[3,] 0.93 0.01 0.06 0.92 0.01 0.07
[4,] 0.83 0.17 0.00 0.81 0.19 0.00
[5,] 0.82 0.18 0.00 0.81 0.19 0.00
[6,] 0.95 0.01 0.05 0.94 0.01 0.05
[7,] 0.74 0.00 0.26 0.70 0.00 0.30
[8,] 0.86 0.14 0.00 0.85 0.15 0.00
[9,] 0.11 0.00 0.89 0.08 0.00 0.92
[10,] 0.87 0.00 0.13 0.85 0.00 0.15
I guess I should've given column names, but this is simple enough I can compare line by line. The probabilities for the first model (columns 1-3) are not identical to the probabilities for the second model (columns 4-6), but they're close enough. I'm pretty sure I did these calculations correctly.
And now we again summarize:
max_prob_simple <- apply(prob_simple, 1, max) choice_simple <- apply(prob_simple, 1, which.max) expected_correct_simple <- sum(max_prob_simple) sd_correct_simple <- sqrt(sum(max_prob_simple*(1 - max_prob_simple))) print(table(choice_simple)) pfround(c(expected_correct_simple, sd_correct_simple), 1)
And here's what we find:
1 2 3 540 239 221 [1] 855.3 10.3
Very close to what we had before. With this new calculation, we expect to get 855.3 correct with a sd of 10.3. So . . .
> 1/pnorm(expected_correct, 899.5, sd_correct) [1] 184458.4
So I'm not playing the game. The odds of winning are about 20 times too low.
If the price to play were 50 cents rather than $10, it would kinda be worth it. Of course I'm not counting the time I spent doing the analysis and writing this post, but that's leisure, not work!
OK, one more thing. To win, you don't quite have to pick which of the three categories is correct; you only have to pick, for each series, whether it comes from the zero-trend process or the nonzero-trend process.
I don't think this will matter much, because if you're willing to guess that a series is negative-trending, it's highly unlikely to be positive trending, and vice-versa. But, hey, we've gone this far, let's define the probabilities in the two-category case:
prob_simple_binary <- cbind(prob_simple[,1], prob_simple[,2] + prob_simple[,3])
And then let's do the calculations again:
max_prob_simple_binary <- apply(prob_simple_binary, 1, max) choice_simple_binary <- apply(prob_simple_binary, 1, which.max) expected_correct_simple_binary <- sum(max_prob_simple_binary) sd_correct_simple_binary <- sqrt(sum(max_prob_simple_binary*(1 - max_prob_simple_binary)))
Ulp. I should've just written a function. Put me in programmer jail for this one.
Anyway, what do we see?
> print(table(choice_simple_binary)) choice_simple_binary 1 2 540 460 > pfround(c(expected_correct_simple_binary, sd_correct_simple_binary), 1) [1] 855.3 10.3
Yup, same as before, just as I expected.
There is one more thing, though: the data are highly autocorrelated, so least-squares regression may not be the most efficient way to estimate these slopes. If we can estimate the slopes more precisely, we can get more discrimination in our predictions. It's hard for me to believe that more modeling will get us much more discrimination here, compared to simple least squares. But, hey, who knows---all things are possible! Play the game if you wan't. But you won't see me plunking down my hard-earned sawbuck.
P.S. You could say that the above all demonstrates Keenan's point, that you can't identify a trend in a time series of this length. But I don't think it would make sense to draw that conclusion from this exercise. After all, you can just tweak the parameters in the problem a bit---or simply set the goal to 800 correct instead of 900---and the game becomes easy to win. Or, had the game been winnable as initially set up, you could just up the threshold to 950, and again it would become essentially impossible to win. Conversely, if Keenan had messed up his calculations and set the threshold to 800, and someone had sent in a winning entry, it wouldn't disprove his claims about climate science, it would just mean he hadn't been careful enough in setting up his bet.
P.P.S. Data, Stan code, and R code are here.
So you can be slightly confident it’s not just noise from looking at the temperature trend alone. I’m assuming the extra certainty we have about global warming comes from the observation that the apparent trend correlates very neatly with other trends in ways that would be expected under a greenhouse gas explanation but would be highly coincidental otherwise? I believe the consensus of climate scientists, just curious.
Presumably the author knew some statistics and therefore that it was not a fair game…but maybe using classical statistics. Are there cases where that could lead you astray and a Bayesian analysis can flip it to a positive expected value? If so, does that tell you something about the class of decision problems where Bayesian analysis is unambiguously superior?
With that kind of introduction, it’s not like one would expect an actually fair contest…
Great post. Loved it.
My only observation is that on prediction contest leader-boards I’ve seen stuff done that I’d have bet was impossible. So, I just have this intuitive feeling that this too can be cracked & will be cracked. And once we do see the strategy adopted by the winning entry we’ll be amazed.
> on prediction contest leader-boards I’ve seen stuff done that I’d have bet was impossible
But those were not based on trying to beat a random number generator (which seems to be the case here.)
Are you saying Andrew’s code has established a hard bound here? In the sense, do we have a black box proof that no strategy can do better than 855, on average?
With knowledge of the random number seed (and program ran) its fully deterministic and without that seed a very good but not completely pattern-less sequence of numbers.
Apart from that all one can try and do is guess the data model they used to generate the series and with the reasonable guess that the prior was .25, .5 and .25, check those both guesses get the posterior and then classify.
Andrew,
you state that you “[..]think the question, “the increase in global temperatures is probably not due to random natural variation,” is fundamentally unanswerable.” Why do you think this? Is it due to some specific characteristics of the global temperatures time series, or is it a wording problem? For example, would be the question “check if the time series of global temperatures can be fit reasonably well by a a statistical model which assumes zero trend in the global temperature” answerable? Maybe it’s obvious, but anyway I’d appreciate a lot if you could give an explanation, either here in the comments or maybe even in a blog post if you feel like it’s a good idea (I do, but I’m biased :-)
I agree with Rahul. It’s a great post. But I do have an issue with your statement in the PS. Those who claim to see trends in these data express confidence levels (however derived) that are much higher than 90, or even 95 percent. So clearly they believe they have a methodology which can pick trended data from untrended data (with roughly this degree of trend) very often. (As you point out, the sign of the trend doesn’t matter very much in this exercise.) Now what I expect has happened is that the actual series looks reasonably strongly like one of the easier lines to classify… but embedded within a hypothetical set of such series, one ought to be a lot more humble about conclusions than being so confident about the one you happened to get. that’s an important lesson harkening back to Kahneman and Tversky.
Knowing Keenan’s previous work with climate data, I suspect at least some of the time series are from an arima(x, 1, 0) model where x is in 0:3. He thinks that the instrumental climate record can be better fitted with an arima(3, 1, 0) model than with a linear trend.
Seeing as the global or N hemisphere temperature record can’t be well fitted with a linear trend (the series is far from linear), that’s not much of a claim on Keenan’s part…
When I looked at that data, I immediately thought it would be arima. I’m surprised Andrew used Stan to fit a model to the slopes rather than taking a time series approach.
John:
I just estimated the slopes using least squares, then I used Stan to fit the mixture model for the distribution of slopes. As discussed near the end of the above post, I have a feeling that least squares isn’t far from optimal for estimating the trends in these lines.
I understood the methodology. When I have a bunch of time series data, my first thought is to look at the PACF and start testing for unit roots. It can be difficult to tell the difference between a unit root (e.g. random walk plus drift) or trend stationary process.
I enjoy these types of applied analysis posts :)
Naive question: Is the result mostly insensitive to the choices cauchy(0,2.5) & normal(1,10)?
Note that Keenan first gave a data set where the trends were distributed like this. After a few weeks he changed it to the one presented in the post above, which much more overlap.
Lars:
Yeah, I wondered about that in his description. Also, upon seeing your comment I clicked on the link and read the thread, which included an amusing line from Richard “Gremlins” Tol: “Why don’t you guys just pay £10 to win £100,000? You don’t need to accept that the challenge has any bearing on climate change — it has not — but it is a great opportunity to make £99,990.”
Tol’s an economist—don’t they teach those guys about expected value? I have a horrible feeling he’s running around buying lottery tickets.
Misconceptions about expected values and lotteries are awfully common, even among relatively educated people – at least judging from the Big Three strategy consultants I know.
By the way, great post. Not only in its regard to the contest or even the subject, but also as an example of that sort of analysis using Stan and R.
By the way (2), I hadn’t read your comment on Noah Smith’s post on “Case-Deaton vs Gelman”. You’re completely right about that too.
In Keenan’s lottery you are only allowed to purchase one ticket max per person. Does that change the payoff analysis, any? I think not but just wondering.
I find all of this to be extremely frustrating. Keenan thinks that world temperature is a random walk (something like the arima(3,1,0) mentioned) but that’s absurd. It only looks like a random walk because he is looking at such a small number of years. A more reasonable model to produce the simulated time series would make getting the 100000 much easier
It actually looks like a random walk because in the last 135 years the climate is messed up. A stable climate should not look like a random walk with a trend. If anyone cares to look, there is temperature data from past centuries; not instrumental data, but it exists.
BTW, the claim that randoms walks are “trendless” processes is one of the fundamental errors in Keenan’s analysis.
No No No No No No No!
I mean, yes, great post, love the analysis, good example for how to use Stan, very clear explanation of why people shouldn’t take the bet, etc., etc.
But Keenan and the whole tenor of this discussion seem to be predicated on the idea that the main evidence for global warming is that there is an upward trend in observed temperatures over the past hundred to hundred-and-fifty years. This completely ignores the fact that we know something about physics, and our understanding of physics also strongly suggests that the earth should be warming. Here’s an old post on the subject.
What Andrew’s analysis (and Keenan’s argument) shows is that you shouldn’t interpret a run of a few decades as telling you very much about the long-term trend in the climate…which is why all of the claptrap about a “hiatus” in the past twenty years is so ridiculous.
Thanks for the link, I am interested in learning more about this topic :)
> But Keenan and the whole tenor of this discussion seem to be predicated on the idea that the main evidence for global warming is that there is an upward trend in observed temperatures over the past hundred to hundred-and-fifty years. This completely ignores the fact that we know something about physics, and our understanding of physics also strongly suggests that the earth should be warming.
+1
> What Andrew’s analysis (and Keenan’s argument) shows is that you shouldn’t interpret a run of a few decades as telling you very much about the long-term trend in the climate… which is why all of the claptrap about a “hiatus” in the past twenty years is so ridiculous.
+1
That is also what Met Office responded to Keenan.
“3) Mr Keenan then goes on to argue that you can only use a statistical model to determine whether the warming we have seen is statistically significant. He argues that the Met Office has used the wrong statistical model and, therefore, our science is flawed.
The study of climate variability and change is broader than the domain of statistics, most notably due to the importance of the underpinning science of the climate system. Our judgment that changes in temperature since 1850 are driven by human activity is based on information not just from the global temperature trend, or statistics, but also our knowledge of the way that the climate system works, how it responds to global fossil fuel emissions and observations of a wide range of other indicators, such as sea ice, glacier mass, sea level rise, etc.
Using statistical tests in the absence of this other information is inappropriate, particularly when it is not possible to know, definitively, which is the most appropriate statistical model to use. In particular, a key test of an appropriate statistical model is that it agrees with everything we know about the system. Neither of the models discussed by Mr Keenan is adequate in this regard. On that basis, this conversation on statistical modelling is of little scientific merit.”
I am curious as to how one separates out the large natural stochastic variation in, say, “global temperature” in a driven dynamical system far from thermodynamic equilibrium from small man-made perturbations?
The issue of metrology, and the proper estimation of systematic uncertainties – errors associated with measurement, dominate such historic time series. Far far less of the planet was instrumented back in 1890.
http://data.giss.nasa.gov/gistemp/graphs_v3/Fig.A.gif
The remarkably small errors bars for, say, 1890 not only strain credulity but toss it in the mixmaster and hit the puree button.
1 sigma ~ 0.1C. Really?
A skeptic experienced in measurement might wonder if the entire field is nothing more than an artifact of the underestimation of systematic errors.
In the context of a model like: “These timeseries probably come from some particular distribution over functions of time which includes lots of other kinds of shapes” getting one particular shape tells you not a lot…
in the context of a model like: “these timeseries come from a set of ODEs determined by physics where the uncertainty is primarily over a small number of physical parameters” you can determine a LOT more from a short time-series. It’s just the strength of the model. You have to believe the model obviously, but if you do, it rules out a crap-ton of other possibilities (like that average temperature might occasionally deviate by 15C for 30 years and then return to its 200 year typical values etc).
Only a small part of GCMs are 1st principle PDEs.
Mostly empirical parametrizations.
Wstimating systematic undercertainty in such mostly empirical models is problematic.
Phil, not only should the earth be warming, it should be so warm that the arctic is ice-free, or should have been ice-free for two years now, according to our esteemed secretary of state. In an op-ed in the Huffington Post in 2009, Kerry wrote: “Scientists project that the Arctic will be ice-free in the summer of 2013. Not in 2050, but four years from now.”
Never mind. Pay no attention to what THOSE scientists said THEN. We have DIFFERENT scientists NOW.
http://www.huffingtonpost.com/john-kerry/we-cant-ignore-the-securi_b_272815.html
Kerry is not a scientist. There was certainly not a scientific consensus that the arctic would be ice-free in the summer of 2013 (or 2016, or 2020, or 2030). There are various scientists saying things like “the arctic could be ice free as early as the summer of X”, but readers should realize that “could” is not the same as “willl,” and “as early as” does not imply “no later than.”
Bruce, that “ice free arctic by 2013” claim is wildly distorted. Specifically regarding Kerry’s statement, PolitiFact rated it “mosly false”: http://www.politifact.com/truth-o-meter/statements/2009/sep/02/john-kerry/kerry-claims-arctic-will-be-ice-free-2013/. Mre generally: http://www.theguardian.com/environment/climate-consensus-97-per-cent/2013/sep/09/climate-change-arctic-sea-ice-delusions
The reason that Keenan is apparently doing this is because he is suggesting that climate scientists are claiming to detect trends in surface temperature datasets using time series analysis alone. This is, of course, a strawman, as this is not what is being claimed. We have a surface temperature dataset that indicates that we have warmed since the late 1800s. Various analyses suggest that anthropogenic influenes are a dominant factor in this warming. This claim is not based on time series analysis of the dataset alone, but on physically-motivated models that are used to try and determine what could explain the observed warming.
Having written this, I see that Phil has essentially made the same point.
This is the best entry ever on this blog. I know, bold claim, but this is EXACTLY the sort of situation that Stan was designed for, and it worked wonders. Anyone can do this without writing samplers. This would be unimaginable just a few years ago; these are truly great times for applied statistical inference.
Why should the data be autocorrelated? Does this imply the data was generated using a random walk, rather than what you are modeling which is random values around a trend? Or am I misinterpreting your Stan code?
I am not a climatologist but my thought is that average yearly temperatures should be stationary with respect to a trend (or no trend).
Ben:
The data pretty much had to be autocorrelated because Keenan sent he simulated the series from a trendless process, but almost all of the series had clear trends. Also I ran acf() on the individual series and found autocorrelation.
This is my confusion. My naive view of global temperature(T) over time t says
T(t)~Normal(mu,sigma)
mu~bo + b1*t
is the correct model, random variation around a trend. What he seems to be simulating is
T(t)~Normal(mu, sigma)
mu~T(t-1)
Or
mu~T(t-1) + b1*t
Maybe I don’t know enough climate science. But I would think the later would be much harder to distinguish while also being the wrong model.
Related – http://www.giss.nasa.gov/research/briefs/hansen_17/
Keenan screwed the pooch in his original data set See
https://andthentheresphysics.wordpress.com/2015/11/20/a-stupid-100000-bet/#comment-67310
for how it graphed out.
He then changed it to what Andrew shows. Which raises the issue of whether somebunny should take him to court:)
What would be really funny is if someone won $100,000 by cracking the encrypted “answer” file that Keenan has pre-posted online. http://www.informath.org/Contest1000/Answers1000.txt
What we do know about the un-encrypted file is that it had exactly 1000 characters, only ones & zeros & presumably a large number of zeros. So maybe there’s some structure to be exploited.
I wonder if the encryption method he used had some weakness, backdoor etc. Looking at Keenan’s other mistakes it isn’t entirely unlikely that he chose a flawed / weak encryption scheme.
Or maybe just try your luck brute force-ing it on a cluster or GPU. At least you don’t have to pay $10 for every try. :)
Rahul:
500 zeroes, 500 ones, is what I’m guessing. But the number of zeroes and ones might be a random variable.
But I’m guessing that if someone does crack the code, that Keenan will find a way to avoid paying the $100,000.
The fact that Keenan posted the “encrypted” answer file shows that he knows nothing about crypto as well… Unless he proves that the scheme he used is secure against a chosen plaintext attact, then given a desired plaintext and ciphertext, it could be trivial for him to calculate a key that would generate said ciphertext from the plaintext (I.e. using a one time pad). If he really wants to prove that there is an answer, then he should use a zero knowledge proof system instead of this meaningless jumbo of characters.
It would be interesting to try to use the possible plaintexts as an additional data source for improving the results! Any info on what method was used to encrypt?
David, after making some effort at this I don’t think there is any reason for such games. You can create your own simulated dataset where you know for sure the overlapping distributions and it is difficult to guess 90% correct. If it weren’t for people brute forcing the seed I think he could even release the actual code used to generate the data.
I wasn’t implying that the encrypted answer can be used to help solve the problem – quite the opposite. My argument is that the encrypted answer file serves absolutely no purpose. It doesn’t prove that a correct answer actually exists (I.e. Keenan isn’t just shooting down every response), and it doesn’t reveal anything about the answer.
> I have argued that there is no observational evidence for global-warming alarm: rather, all claims of such evidence rely on invalid statistical analyses.
??? Really?
Bite me – http://berkeleyearth.org/summary-of-findings/
Bite me – https://www.ipcc.ch/publications_and_data/ar4/wg1/en/figure-9-5.html
Bite me – http://newscenter.lbl.gov/2015/02/25/co2-greenhouse-effect-increase/
Now where’s my $100k?
Oh, and for good measure, see the refs here – http://bartonlevenson.com/ModelsReliable.html
Wasnt Keenan’s point that the model used in the IPCC report to model the trend was not adequate (?), and therefore the CI’s were underestimating uncertainty, and his take was something like we can’t conclude there is a trend from observational data, because of this uncertainty? What are your opinions on this? It certainly looks like there is trend from “eye-balling”, but was the statistical analyses in the IPCC really invalid or his point doesnt make sense?
Keenan’s statements are grounded in ignorance not understanding. If all we had was temperature vs time and no knowledge of physics then perhaps he’d have a point. If you turn a blind eye to everything we know except temperature vs time then no doubt all sorts of creative analyses appear plausible.
Well ok, but to be fair he is not claiming “global warming is not real”.
What are your opinions on this? It certainly looks like there is trend from “eye-balling”, but was the statistical analyses in the IPCC really invalid or his point doesnt make sense?
His point doesn’t make any sense. It is clear that the surface temperature data indicates that we are warmer now than we were in the mid-1800s. The IPCC’s analysis is simply a linear trend analysis with a confidence interval that is determined by assuming that the residuals are correlated. I do not think that there is any possible valid analysis that would lead us to conclude that we haven’t warmed. However, the IPCC’s analysis is not (as Keenan appears to be suggesting) claiming that there is actually some kind of linear trend hidden in the data itself; it is simply determining the best-fit linear trend and the uncertainty in that trend. A proper attribution study (i.e., attempting to determine why the data has the form that it is) requires comparisons with physically-motivated models.
I tried to do the same analysis in PYMC, for learning purposes. I am a complete newbie. I did not get as good results – it seems my model does not really converge to a good solution. Here’s the complete notebook: https://www.dropbox.com/s/q2x1lbpwkl3ed3p/Contest1000.html?dl=0
Very interesting that pymc did not come nearly as close. I’d be very interested to find out why and to see if pymc3 could give a better fit using NUTS. Also pymc3 supports Gaussian Random Walk stochastics which could be useful on this data.
If you want to read about my motivation for the Contest, see my critique of the statistical analyses that are in the IPCC Assessment Reports. As stated on the Contest web page, the “critique concluded that the statistical analyses are seriously incompetent, and further, that no one has yet drawn valid inferences, via statistics, from climatic time series”.
There is support for the global-warming hypothesis from computer simulations of the climate system (GCMs). The Contest, and my critique, are not about those; they are about statistical analyses of observational evidence that are independent of climate simulations.
Even if someone does find a way to win the Contest, it will not be by using any of the statistical methods that have been used in climate science. The statistical methods that have been used in climate science are not suitable for climatic time series, for reasons explained in my critique.
Andrew said “the evidence for climate change does not come from any single series but rather from many sources”. The different observational series are often correlated with global temperatures. Moreover, the support from any given series is extremely weak, at best.
Lastly, I thank Andrew for not trying to game the Contest and for approaching the Contest as it was intended: as a question pertaining to statistical inference.
Douglas,
The Contest, and my critique, are not about those; they are about statistical analyses of observational evidence that are independent of climate simulations.
As has been explained to you many, many, many, many, many, …….. times, there is no claim about anthropogenic global warming that is based only on statistical analyses of observational data. The basis for your competition is a massive strawman, something that you are apparently an expert at savaging.
Naive question: Is it right to interpret what you write as meaning that *all* serious AGW arguments based on structural / domain models that might used observational data to fit parameters but the underlying model is always Physics-ey never a purely time-series / black box / functional model?
Yes, I would think that is true. I can’t think of a single example of a causal claim about an observation that isn’t based on some underlying understanding of the physical processes that influence the system being observed.
It was certainly true back in the 1990s, when i was helping design supercomputers and having long discussions with climate modelers about what they were doing, or hearing people talk about attribution studies or looking at Bill Ruddiman’s work.
Ststistical analysis can help in finding interesting patterns, but those better lead to physical mechanisms that work.
Lot of prediction that goes on in applications from spam detection to recommendation engines to finance to ad-display seems to work well with purely statistical models with little underlying domain input.
So, might it be possible to successfully achieve the lesser goal of purely predicting climate (rather than understanding it) using statistical analysis devoid of underlying physics-models?
Intuition tells me “NO” but I’m trying to understand why black-box models work well at prediction on some problems but not on others? Is it that we have a lot more training data in finance or spam but not so much for climate?
I think one thing is that we measure “work well” generally in terms of some decision theory aspect. Like for recommendation engines, they increase sales by some amount of dollars/yr
The goodness of the model can be assessed on a relatively short timeframe, and the consequences of model failure are relatively trivial compared to say total annihilation of the human race via a massive climate change induced warming.
We’ll only know the goodness of climate models in a couple hundred years, and we’ll have no second, third, fourth, or 120th chance to alter the models post-hoc.
In my eyes it is an attempt at obfuscation: minimize statistical significance in order to hint that it has not warmed significantly. It clearly has warmed regardless of whether the underlying process is trendless or not. But… We have observed increasing greengrocers has concentrations. Physics allows us to assign zero prior probability to a process with stationary mean. It is a question of estimating the uncertainty of the sensitivity or in this case the trend. It is not a question of p-values. Mitigation skeptics argue for large uncertainties in the trend in order to claim the warming is not significant, while at the same time arguing for a short tailed uncertainty on climate sensitivity because that minimises the expected cost. (see http://statmodeling.stat.columbia.edu/2015/12/10/28302/ )
You cannot have it both ways, and as Victor Venema recently argued on his blog uncertainty is not your friend.
http://variable-variability.blogspot.com/2015/12/judith-curry-uncertainty-monster-high-risk.html
Someone said that physics tell us that Earth should be warming up. However, physical models are, in general, built to explain the observed events, and the physicists basically invent some underlying mechanism (generator model) that matches, according to some criteria, the observed world. Many hidden principles are used, for instance, the equivalence principle which considers that some events are equivalent in some sense. All the intrinsic difference among those events are taken for granted to build the so-called physical model, otherwise it would be impossible to build a reasonable physical model.
I am not claiming that the Earth is not warming up. What Keennan seems to argue is the obvious: we’ll never know the mechanism behind the observable world, what we have are just observed data (and graphics) and based on them you can build your (physical, statistical, biological, geological, etc) model.
The real problem is that the measurement device is model dependent and the model is measurement-device dependent. Time is also model and measurement-device dependent, and vice-versa. This complex symbiosis causes confirmatory biases, since models, measurement devices and time are continually adjusted to have the best match possible. I am not saying that physical models do not work. They work in a very specific domain and the word “work” has a very specific meaning.
People think that time is independent of the measurements, and predictions are different than descriptions. However, time is measured through a measurement device that has “known physical laws”, i.e., the measured time, the chronometer, which is used to make predictions, is a by-product of the observed world. That is, you use measurements to compare measurements. In any physical model, you can remove time as a primitive concept; the question is: physics make predictions or just descriptions that satisfy some criteria?
Well, if people reject conservation of energy and Greenhouse Effect and other well-known physics, yes there’s no explanation.
On the other hand:
Spencer Weart
The Discovery of Global Warming.
or, as Adm (ret) David Titley testified yesterday in Senate,
“We certainly still have questions on the details like tornados, like typhoons, but we kind of understand the basics. I mean, this is cutting-edge 19th-century science.”
Oops sorry, that was from 2013, but he said the same thing yesterday.
If you read that carefully, and also look at the full Met Office report, you will see that they are not disagreeing with my position. My position is that all the purely-statistical analyses of climatic data are untenable. The Met Office report does not really argue against that. Instead, they cite computer simulations of the climate system, to support their belief in the global-warming hypothesis: that is changing the question.
The Met Office response to my criticisms is discussed in my critique of the IPCC statistical analyses. For more details on this, see that critique.
The IPCC, and thousands of research papers, use purely-statistical analyses for many of their conclusions. You can readily confirm that. Some people try to misrepresent that—it is obvious why.
My prior comment, at 11:44 am, was intended to be in reply to Lars Karlsson, at 11:25 (and I had clicked on the Reply link).
Interesting. Can you list some of the papers using purely-statistical analyses for their conclusions? Even better if the said paper is referenced by IPCC.
PS. I’ve no dog in this fight, but if such papers are indeed used by IPCC then that would contradict what “…and Then There’s Physics” &@John Mashey write above.
Of course, it would still say nothing about the overall conclusions regarding AGW just about one kind of evidence.
I think there may indeed be some papers that do purely statistical analyses. I can think of one, but that was trying to establish if recent trends were statistically different from long-term trends, not trying to determine the causes of the observed warming. I do not think that there are any that use the temperature datasets to infer the causes of warming that do so using statistical analyses only. I’d certainly be very surprised if any such papers exist.
> I do not think that there are any that use the temperature datasets to infer the causes of warming that do so using statistical analyses only. I’d certainly be very surprised if any such papers exist.
1. If Mr. Keenan is suggesting that there are then he needs to list them.
2. Eli noted a while back “Data without a good model is numerical drivel. Statistical analysis without a theoretical basis is simply too unrestrained and can be bent to any will.” If the foo shits…
> The IPCC, and thousands of research papers, use purely-statistical analyses for many of their conclusions.
That’s not even wrong.
Coming into this argument, it appears that Andrew has shown that with this distribution, I will pick the correct answer for the trend about 85% of the time. Thus it would appear that unless I have prior information that global-warming is less likely than the other hypothesis (i.e. 50% prior), then unless in haste I have slipped into a fallacy, this implies if I bet against global warming I will be wrong 85% of the time.
Is the mitigation cost so high we would want to do nothing and be wrong 85% of the time?
A good place to start is with the most-recent IPCC Assessment Report: Climate Change 2013. In that Report, Chapter 2 is devoted to atmospheric observations: see especially Box 2.2, which is subtitled “Trend models and estimation”. You can then check any of the relevant references cited in the Chapter. Other chapters on observational evidence are similar.
Chapter 2 is discussed in my critique, as is Chapter 10, which is devoted to detection and attribution of climate change. As my critique notes, at the time of writing, the sole work that attempted to provide a physical justification for choice of statistical model was due to Koutsoyiannis [2011].
About “…and Then There’s Physics”, that is Ken Rice, from Edinburgh. He has a reputation for posting comments that are misleading and disruptive, and he has been banned from at least one blog for that reason.
I’m aware of being banned from one blog, but that was after pointing out that what the author had posted was not true. Could be regarded as distruptive, I guess. However, none of that changes that your challenege has little – if any – relevance to the analysis of surface temperature datasets, espectially when it comes to actually understanding why the data has the properties that it has. That you can find some randomly generated dataset that happens to match the observed data tells us virtually nothing. Of course, you could do such an analysis so as to determine some properties of the data, but I don’t think you’ve ever answered my question as to what such analysis would actually tell us that might be of some use.
“In essence, the prize will be awarded to anyone who can demonstrate, via statistical analysis, that the increase in global temperatures is probably not due to random natural variation.”
[…]
“A prize of $100 000 (one hundred thousand U.S. dollars) will be awarded to the first person who submits an entry that correctly identifies at least 900 series: which series were generated by a trendless process and which were generated by a trending process.”
http://www.informath.org/Contest1000.htm
Can you clarify which of these criteria determine the prize?
Thank you Andrew for such an exceptional post. What an awesome tour de force!
To my fellow readers : I would love to find someone here who can informatively discuss and tutor me on many of the nuances in Andrew’s technical posts, such as this one. Prior teaching experience a must, with at least an MS in Statistics or closely related (Physics, etc). Upper end, private-tutor hourly rate. Assumed long distance -> Skype + Paypal. Please write to me at Gmail, with your CV attached.
https://xkcd.com/793/
Replace “physicists” with “statisticians”? ;-)
Figure 1 is some Dragon Ball ****!
Douglas J. Keenan did not make a fair analysis of the global temperature by only comparing two models, namely ARIMA(1, 0, 0)+trend and ARIMA(3,1,0)+trend.
The method of taking first difference of a time series is in many cases used to create a stationary time series in economics and finance.
Taking first difference of the global temperature is not appropriate since nothing indicates that the global temperature is not stationary – at least for the last 200 years. In addition to this, the ARIMA (3,1,0)+trend violates the first law of thermodynamics.
There are several possible models one can use. I have been looking at the models ARIMA (k, j, 0) for k = 1, .., 7 and j = 0,1. The best fit according to AIC-logic and Box_Ljung test is ARIMA (4,0,0).
Common to these models is that they give virtually the same trend with slightly different confidence intervals. Some of the ARIMA(k,1,0)+trend shows a significant trend.
This applies to both NOAA 1880-2015 and 1850-2015 HADCRUT.
AIC-table for NOAA
https://www.dropbox.com/s/atag4e6mjgbm6kg/NOAA%201880-2015%20%20ARIMA-models.jpg?dl=0
AIC-table for HADCRUT
https://www.dropbox.com/s/um1x5bdqh3s844p/HadCrut%201850-2015%20%20ARIMA-models.jpg?dl=0
A scientist is committed to the principle of Utmost Good Faith. This means that he must give a fair and balanced presentation of his scientific results. There is some way to go before Doulas J. Keenan is there.
Douglas J. Keenan 1000 series contest is described in the following link:
http://www.informath.org/Contest1000.htm
He is not stating directly that he is using ARIMA (3,1,0) + trend model in the simulations. However from several discussions it is likely that he is using ARIMA (3,1,0) + trend model.
In order to check if the assumptions hold, I have performed the Box-Ljung test on the residuals for each of the 1000 series. If Douglas J. Keenan has simulated an ARIMA (3,1,0) + trend model, the distribution of test probabilities will follow a uniform distribution on the interval [0, 1]. Jf. The R-program: ARIMA-procedure.
The results are shown in the following graphs:
https://www.dropbox.com/s/yk1kdk0czl1h8e9/HadCrut%201850-2014%20Box-Ljung-test%20ARIMA%283%2C1%2C0%29%2Btrend.jpg?dl=0
It is clear, that the distribution is not a uniform distribution. It is right skewed.
This means he is not using the ARIMA (3, 1, 0) + trend model or he is doctoring the simulations to confuse the participants in the contest.
This post is good up to the point where the author drops the ball with
his first postscript.
As ‘Jonathan (another one)’ points out in an early comment:
“Those who claim to see trends in these data express confidence levels (however
derived) that are much higher than 90, or even 95 percent.”
And that’s the whole point of the exercise. Douglas Keenan set a threshold
of 900. But he is being unnecessarily generous. He could have set it to to
950.
Because if it’s not possible to do this exercise to an accuracy of at least
950 then that invalidates at least some part of a number of papers that have
been published.
Do we see the authors of those papers retracting their papers? Why not?
Do we see papers or comments being published in the climate science literature
criticizing those prior papers for this error? No, we do not. The question
is why isn’t such criticism being published by the journals in the field?
I don’t know how long it took Andrew Gelman to write this post but I get
the impression he’s so skilled at this sort of thing that we are talking a time
measured in hours.
He doesn’t need to use Douglas Keenan’s series but can easily generate his own,
with whatever properties he deems appropriate, and then test that system that is
completely under his control as to whether it’s possible to separate the trended
from untrended to an accuracy greater than 950.
If not, then that would form the basis for a good paper since it invalidates
previous work.
Surely climate change is an important enough subject that is worth doing correctly.
Mandrewa:
950 has nothing to do with it. Tweak the parameters and you can correctly identify 850 series, or 950 series, or whatever. It’s all arbitrary and I don’t see it having any relevance to climate change.
But of course I think climate change is important, and my colleagues and I have written a paper on how difficult it is to reconstruct climate from tree-ring data: http://www.stat.columbia.edu/~gelman/research/published/ClimRecon.pdf
It could be I’m missing something important. In fact that’s
even probably the case.
But as I understand it the context is that we have papers
that depend upon being able to distinguish random data from
data that has trends in it.
And for these papers to actually work they need to be able
correctly distinguish trended data from purely random data
to some high level of accuracy.
And for these papers to actually work they have to be able
to do this with just one try.
In your comment above I believe you’re asserting that it
would take you 200,000 guesses or bets before there was
a decent chance that one or more of those bets was able
to distinguish the trended data from random data with 90% or
better accuracy.
So clearly if it would take 200,000 guesses to find one
guess (assuming an omniscient observer that answers questions)
that distinguishes between trended and random data
with 90% accuracy, then logic that depends upon distinguishing
trended from random with just one guess is going to fail.
The validity of this argument depends upon the synthetic
data that Keenan generated having similar statistical
properties to real world data. I assume that it actually
does because if it didn’t more people would be criticizing
the argument on that basis.
No, I think this is the bit that isn’t true. We essentially have one system (our planet) for which we have managed to estimate the time evolution of global surface temperatures (we do have more than one group producing this, so we don’t strictly have only one dataset, but they are all attempting to represent the same system over the same time interval – okay, some go back a bit more than others, and they don’t all have the same coverage). Given that data, it is possible to then use statistical analysis to determine some properties of the data, such as the linear trend, and the uncertainty in that trend. In this context, this is not claiming that the data has a trend in it, or not; it is simply estimating the linear trend, given the data. The reason we think it is not simply random is not because we can determine a linear trend, it is because our understanding of the physics of our climate (and how it response to changes) means that it cannot simply be random.
Carbon dioxide is a greenhouse gas. Therefore as its concentration in the atmosphere increases there has to be a warming trend added to the temperature series that would have occurred in the absence of an increasing amount of carbon dioxide.
That does not mean that average temperatures would actually increase though. It could have been that without man, temperatures would have been dropping due to these other factors, and thus that adding additional CO2 would have just moderated that fall in the short time we have been observing.
Although it may be simple to calculate the amount of energy absorbed by a given amount of CO2 in clear air, the actual net impact on the climate is not necessarily simple to calculate. We might imagine that we can model the carbon dioxide by adding a simple linear term for the energy added to the atmosphere by the additional CO2. Or maybe we know it’s not a linear term actually, but really a logarithmic term because as the concentration increases the amount of additional energy per added CO2 molecule drops.
Both of those situations would be simple and straightforward to model, at least as far as CO2 is concerned. Where it might get complicated is if some of the other factors determining climate are non-linear. An obvious candidate would be water. Now the water molecules don’t care where the additional energy is coming from, but if the water in the system responds by increasing its concentration in the atmosphere in response to the added energy from the CO2, and then in turn that added water changes the odds of clouds forming, then this changes a lot of things.
More clouds means simultaneously some energy trapped beneath clouds that would have otherwise been emitted to space as well as quite a bit of energy coming down from the sun that is reflected back to space and lost from the atmosphere and earth. Although the energy impact of a particular cloud depends on where it is with respect to the sun, still overall clouds on average are going to reduce the energy in the atmosphere.
So now we have negative feedback.
It’s not a linear system anymore and it’s very hard to model.
I don’t believe any of the climate models are even close to modeling that simple system of two gases that I just loosely described.
So yes, I agree, some of the physics is straightforward. There has to be a warming for instance. That is with respect to the background climate whatever is. I doubt we actually know that background climate by the way.
But beyond that it gets complicated fast. The actual added warming for a given amount of CO2 for instance is probably not a simple term. If we really understood this it’s probably a complicated function of a number of factors and including the current temperature. That is I would guess the added energy would be greater for a lower temperature than a higher temperature.
None of what I just said has anything much to do with the challenge that Douglas Keenan posed, except that I can easily imagine that our signal or trend that we are trying to pull out is too small in the context of other fluctuations and that we cannot practically separate out the CO2 signal in the real climatic data. Or to say it another way, the actual data which is the combined product of all factors, not just CO2, looks like pseudo-random numbers passed through an algorithm.
mandrewa,
I don’t know how to respond to your comment other than to point that people have spent a great deal of time considering the very questions you posed. Although science can’t provide definitive answers to these questions, given the complexity of the system, our understanding is better than you seem to be willing to recognise.
An extract from the Contest web page is below.
Thus, the parameters are constrained, and there is important relevance to the global-warming hypothesis.
Relatedly, the Contest ended yesterday. No winning entry was received.
Doug,
No, there really is virtually no relevance to the global warming hypothesis. What you call the Met Office Model is really just a data analysis technique. It allows us to determine the linear trend in the data, and the uncertainty in that trend. By itself, it tells us nothing else. Our understanding of global warming is based on our understanding of the physics of our climate and how it responds to changes. You can of course, choose to analyse the data in some different way (using random walks, for example) but finding some random walk that happens to fit the data tells us almost nothing and, despite asking a number of times before what it does tell us, you have yet to answer that question.
Regarding statistical models generally, such models are always used when drawing inferences in statistics. For example, when the IPCC (or Met Office) inferred, via statistics, that temperatures are increasing more than could be reasonably attributed to random natural variation, that required a model. The IPCC acknowledges this in its most-recent Assessment Report. For a detailed discussion of all that, see my critique of the IPCC Report. For something brief and very general, see the Wikipedia article “Statistical assumption“.
For blog readers who are unfamiliar with “…and Then There’s Physics”, he is Ken Rice from Edinburgh. He spends much of his time commenting on the internet, in response to anyone who does not agree with his alarmist position on global warming. Most of his comments are disinformative, as here.
Separately, some Remarks on how the Contest ran are now posted on my website.
“Now that the Contest has closed, I intend to investigate my legal options regarding libel.”
Doug,
Yes, determining if the temperatures are increasing more than could be reasonably attributed to random natural variations does require a model. However, it is not a model that relies only on statistics, which is something that you still seem incapable of grasping. Continuing to claim that it is, does not make it true.
It’s true that I do sometimes comment in response to those who promote scientific ideas that are almost certainly wrong. I’ve never, on the other hand, accused anyone of libel if they happen to disagree with me. Have you?
@ Ken Rice (“and Then There’s Physics”)
To infer, via statistics, that temperatures are increasing more than could be reasonably attributed to random natural variation requires a statistical model. That is basic in statistics. (And the links included in my prior comment discuss that.)
This is a statistics blog. The blog proprietor is a distinguished statistician, and many blog readers are also quite knowledgeable about statistics. Those people know what statistical inference is, and they also know that such inference requires a statistical model. Ergo, your attempts at disinformation here will fail.
Your standard method of operation is to harangue with drivel until people get tired of you. Doubtless, you will continue that here. You will, though, fail at your goal of disinformation.
Doug,
No, this is wrong, and very obviously wrong. All changes in our climate are caused by something. Some of the changes will be due to internal variations and we might regard these as random natural variations. Some of the changes will be due to external influences (the Sun, volcanoes, emission of CO2 into the atmosphere). To understand how much can be reasonably attributed to what you call “random natural variations” requires a model that describes these “random natural variations”. Such a model cannot simply be a statistical mode. It has to be a model that also considers the relevant physics. That you can find a statistical-only model that happens to fit the observations better than the simple linear fit used by the Met Office (which is really a data analysis technique, rather than a model) does not mean that the observed changes are more likely due to random natural variations, than due to anthropogenic influences (in truth, it’s a combination of the two, but that’s beside the point). We’re dealing with a system for which we understand the underlying physics. A model that completely ignores the underlying physics tells us nothing about what is causing the changes that are observed.
I notice you didn’t answer the question I asked at the end of my previous comment.
Actually, since we all focus on this sole question “Are we causing global warming?” I think the equally important other question gets little attention:
“Even if we are causing GW should we be doing anything about it?”
I think people take the 2nd part as axiomatic. But I think that’s where the real debate ought to lie today.
It gets little attention because the best political rhetoric to stop something from being done about it remains to doubt that we are causing it.
You see this sort of tactic all the time in political disagreements. Battles over what the facts are and what the evidence says are mere proxy wars, masking that the real disagreement is about values and objectives.
Rahul,
I agree. That it is happening and that it is mostly us does not tell that we should do something about it or – if we should – what that should be. The real debate should really be about this, not about whether or not a statistical model alone can indicate how much is due to random natural variations (it can tell you nothing). As Anon suggest, the problem is the sowing of doubt that leads people to consider there is nothing happening and, hence, that nothing needs to be done.
Personally I’m in that camp: I believe AGW is real. But I don’t believe we can or should be doing much about it.
But I find this a very minority position. It almost gets no mention in the typical debate. It’s almost more politically correct to deny AGW than to accept it & refuse action. It’s rare to even find smart blogs discuss this position.
I find that sad.
Rahul,
Why do you think we can’t, or shouldn’t, do anything about AGW, despite accepting its reality?
With any reasonable discounting function I cannot justify the sacrifices they ask of the current population.
e.g. Take India. Recently there was an uproar over the massive number fossil fuel plants that we will be building over the next decade & how much CO2 it may release.
With so many daily existential problems facing the median Indian many of which need development as an imperative to resolve how can I bring myself to ask him to sacrifice for the cause of some remote generation in the future?
Till we substantially solve things like starvation, malaria, malnutrition, et cetra I think it is ethically wrong for a nation like India to spend any resources on mitigation measures against AGW.
@Doug
For arguments sake, were you convinced that AGW is for real: would you then advocate that we do something about it? Or not really.
Just curious.