Raghu Parthasarathy presents a wonderfully clear example of disastrous p-value-based reasoning that he saw in a conference presentation. Here’s Raghu:
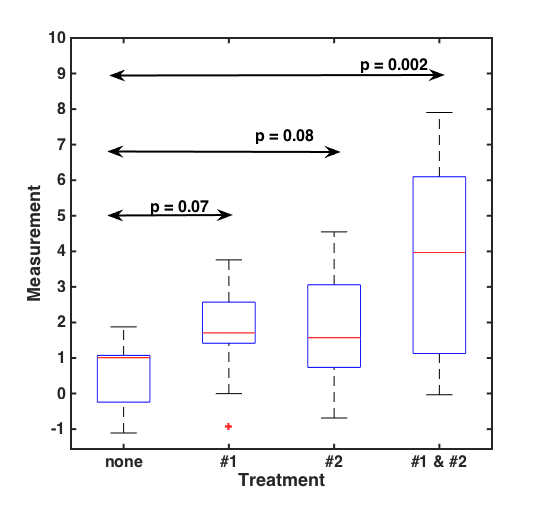
Consider, for example, some tumorous cells that we can treat with drugs 1 and 2, either alone or in combination. We can make measurements of growth under our various drug treatment conditions. Suppose our measurements give us the following graph:
. . . from which we tell the following story: When administered on their own, drugs 1 and 2 are ineffective — tumor growth isn’t statistically different than the control cells (p > 0.05, 2 sample t-test). However, when the drugs are administered together, they clearly affect the cancer (p < 0.05); in fact, the p-value is very small (0.002!). This indicates a clear synergy between the two drugs: together they have a much stronger effect than each alone does. (And that, of course, is what the speaker claimed.)
I [Raghu] will pause while you ponder why this is nonsense.
He continues:
Another interpretation of this graph is that the “treatments 1 and 2” data are exactly what we’d expect for drugs that don’t interact at all. Treatment 1 and Treatment 2 alone each increase growth by some factor relative to the control, and there’s noise in the measurements. The two drugs together give a larger, simply multiplicative effect, and the signal relative to the noise is higher (and the p-value is lower) simply because the product of 1’s and 2’s effects is larger than each of their effects alone.
And now the background:
I [Raghu] made up the graph above, but it looks just like the “important” graphs in the talk. How did I make it up? The control dataset is random numbers drawn from a normal distribution with mean 1.0 and standard deviation 0.75, with N=10 measurements. Drug 1 and drug 2’s “data” are also from normal distributions with the same N and the same standard deviation, but with a mean of 2.0. (In other words, each drug enhances the growth by a factor of 2.0.) The combined treatement is drawn from a distribution of mean 4.0 (= 2 x 2), again with the same number of measurements and the same noise. In other words, the simplest model of a simple effect. One can simulate this ad nauseum to get a sense of how the measurements might be expected to look.
Did I pick a particular outcome of this simulation to make a dramatic graph? Of course, but it’s not un-representative. In fact, of the cases in which Treatment 1 and Treatment 2 each have p>0.05, over 70% have p<0.05 for Treatment 1 x Treatment 2 ! Put differently, conditional on looking for each drug having an “insignificant” effect alone, there’s a 70% chance of the two together having a “significant” effect not because they’re acting together, but just because multiplying two numbers greater than one gives a larger number, and a larger number is more easily distinguished from 1!
As we’ve discussed many times, the problem here is partly with p-values themselves and partly with the null hypothesis significance testing framework:
1. The problem with p-values: the p-value is a strongly nonlinear transformation of data that is interpretable only under the null hypothesis, yet the usual purpose of the p-value in practice is to reject the null. My criticism here is not merely semantic or a clever tongue-twister or a “howler” (as Deborah Mayo would say); it’s real. In settings where the null hypothesis is not a live option, the p-value does not map to anything relevant.
To put it another way: Relative to the null hypothesis, the difference between a p-value of .13 (corresponding to a z-score of 1.5), and a p-value of .003 (corresponding to a z-score of 3), is huge; it’s the difference between a data pattern that could easily have arisen by chance alone, and a data pattern that it is highly unlikely to have arisen by chance. But, once you allow nonzero effects (as is appropriate in the sorts of studies that people are interested in doing in the first place), the difference between p-values of 1.5 and 3 is no big deal at all, it’s easily attributable to random variation. I don’t mind z-scores so much, but the p-value transformation does bad things to them.
2. The problem with null hypothesis significance testing: As Raghu discusses near the end of his post, this sort of binary thinking makes everything worse in that people inappropriately combine probabilistic statements with Boolean rules. And switching from p-values to confidence intervals doesn’t do much good here, for two reasons: (a) if all you do is check whether the conf intervals excludes 0, you haven’t gone forward at all, and (b) even if you do use them as uncertainty statements, classical intervals have all the biases that arise from not including prior information: classical conf intervals overestimate magnitudes of effect sizes.
Anyway, we know all this, but recognizing the ubiquity of fatally flawed significance-testing reasoning puts a bit more pressure on us to come up with and promote better alternatives that are just as easy to use. I do think this is possible; indeed I’m working on it when not spending my time blogging. . . .
I don’t see any fatal flaws to p-value reasoning, used correctly, in relation to discrepancies from the null. Unless one is clear about that, it’s best to use the N-P set-up, which still requires something like a severity interpretation which is in sync with both Fisherian and N-P tests. CIs could only be thought to magnify effect sizes if you misinterpret the width of the interval as indicative of effect sizes which is silly.
I think the idea behind the claim that classical confidence intervals overestimate magnitudes of effect sizes is that they have “biases [in the colloquial sense] that arise from not including prior information” and are thus both too wide and centered too far from zero.
Does anyone know of a good example of study (either real or hypothetical but realistic) where the bias with confidence intervals is not trivial?
I’m also wondering whether the criticism 2a) is only true for confidence intervals or concerns interval estimates more generally.
Pierre:
There are zillions of examples. Just about any published result based on a noisy study and p less than .05. Power pose, embodied cognition, himmicanes, beauty and sex ratio . . . the examples are endless. Just open any issue of Psychological Science published between 2010 and 2015. If you want a single example, consider that study that claimed that single women were 20 percentage points more likely to vote for Barack Obama at a certain time of the month, compared to the corresponding change among married women. The confidence interval there would be 20% +/- 8% or something like that. Any true effect would be in the neighborhood of 2% or less. Huge bias. John Carlin and I discuss this in our paper on type M and type S errors.
Pierre:
I find this helpful – http://statmodeling.stat.columbia.edu/2016/08/22/bayesian-inference-completely-solves-the-multiple-comparisons-problem/
In two ways.
More obvious is the subset of p < .05 studies.
Perhaps less obvious is the the standard CI procedures follow from what would be ideal for applications where it is expected (based on current scientific understanding) that extremely large positive and negative effects are just as likely as tiny effects. That is, they result from assuming priors for effect size like that – this brings into question whether the seemingly good property of uniform coverage that standard CI procedures here are good for what?
(By the way, it is not something you can see in a single study in isolation – its a repeated application property.)
I’m a bit confused by the example. Raghu says that the #1/#2 effect he simulates is not interactive, but then he says that the mean of the simulated #1/#2 effect is equal to the mean of #1 times the mean of #2. Isn’t that the very definition of a strong interaction? I.e., if the true treatment effect of both drugs combined is equal to the product of each administered singly, then that is a noticeable difference to report, p-values or no p-values. Interactions can certainly have ambiguous effects on p-values, but I don’t quite follow this example.
I wondered about this too. But also, perhaps it is based on just what the measurement of tumor growth is — whether it’s an additive or multiplicative scale. If it’s an additive scale, then one would expect that the effect (assuming no interaction) would be additive — which in this case would still give mean 2 + 2 = 4 — so the particular numbers here are a poor choice to make a distinction between additive and multiplicative.
Related: The ANOVA definition of “interaction” does depend on scale; I think a lot of people aren’t aware of this. One can sometimes “remove” an interaction in ANOVA by taking logs of the original measurements.
Bob: certainly a multiplicative interaction may be important, and as Martha notes, whether one cares about additive or multiplicative effects depends on what it is that one is measuring. (If I cared about the mass of a block, there would be a multiplicative “interaction” between the volume of the block and the density of the material that made it up, but I wouldn’t go on proclaiming some special synergy between the effects of volume and density.) It’s been ages (8 months?) since the talk that inspired my post, but I think the thing being measured was the factor by which some cancer mass changed.
In any case, it’s certainly great and important to figure out if interactions are multiplicative or additive. My point, though, was just that one should never claim that treatment and treatment 2 are by themselves unimportant (because p>0.05 !) while treatments 1 and 2 together are effective (because p < 0.05 !). The sensible thing to do would be to actually make inferences about the interaction between 1 and 2, given the data at hand. This may seem obvious, but, apparently, it's not!
Bob, yes! As a pharmacologist, I can say with confidence that the concept of drug synergy is associated with many poorly designed and misinterpreted experiments. The example modelled here is no exception. The interpretive problem is more to do with the lack of clarity of setting and testing expectations of drug actions than it has to do with statistical crimes.
The non-linear dose-response relationship means that it is impossible to reliably diagnose an interactive effect of two drugs on the basis of the effects of a single dose of each drug. The experimental design is a failure. Statistical issues are not important here.
“The experimental design is a failure.”
GS: I’ll say! Here’s what should have been done: administer each dose of each drug (or whatever #1 and #2 are) to each subject in the study (N can be rather small) at least twice. Then administer each dose of #1 in the presence of each dose of #2 (or, at least, do this for many dose combinations). Plot the D-E functions for each subject. There you go! If you are interested in some effects of #1 and #2 as well as #1 and #2 together, you have your answer! Simple.
I’m with you on that confusion… Are the effects “additive” or “multiplicative”? Or a little bit of both (because of the way the simulation is set up)? I also see a number of other flaws in the argument… ok with the z values but have issue with p?
Yes, this is a dumb mistake…and one that takes down the whole example. By definition a multiplicative effect is a great example of “interactions” or “synergies”.
Mayo: “CIs could only be thought to magnify effect sizes if you misinterpret the width of the interval as indicative of effect sizes”
If you only accept (= ‘publish’) cases where the p-value is low enough (e.g., 0.05), then you get biased effect sizes, because you don’t ever get the smaller ones. Andrew has illustrated this before, and I assume that’s what he means here, too.
It never ends.
Gelman: p values are an attractive nuisance that are almost always used incorrectly.
Mayo: Not if you use them correctly.
So what exactly is “correctly”? (Q for Mayo really)
Correctly means that the null hypothesis is deduced from the theory you care about. For example, a device like the EM drive should produce zero net thrust, this SIR model predicts another outbreak next November to February, that surface will emit IR proportional to the 4th power of it’s temperature, etc.
In those cases p-values may not be ideal but I do not really see a problem in practice. If there is one, it is so minor compared to the real problem it can be ignored for now. It is NHST, where the null hypothesis is *not* deduced from the theory/model, that is pseudoscience. The only use for that is to affirm the consequent, transpose the conditional, and torture small animals.
So pretty much impossible to use p-values “correctly” in a medical context?
Not at all, I gave the SIR example… You can also check out the Armitage-Doll model but implement without assuming the errors that lead to cancer are rare. What would be the age of peak incidence? I could go on, but check that first.
Tom, the fact that you imply Mayo would support the notion that a small P-value in isolation provides a license to publish indicates that you are completely unfamiliar with Mayo’s philosophy.
Suppose the following sequence instead of the one laid out by Raghu Parthasarathy:
We START with Treatment #1 and Treatment #2 together and obtain a small p-value (his .002). Now what? Are we tempted to look at Treatment #1 and Treatment #2 individually or do we leave well enough alone?
There’s something off about Raghu’s example here. If the combined effect is multiplicative, then the combined variance wouldn’t be the same as for either of the components. His description said the noise is the same as (although the plot shows more noise than) each component.
The s.d. of the product would be 1.5 (i.e., fractional variance of product = sum of fractional variances of individual components).
Since it looks from the plot as if the combined s.d. is larger than that, probably the p-value of the combined treatment would be even lower.
I should think about this a bit more, but two things to keep in mind are:
(1) there are many different ways one could imagine the variance to behave, depending on what the experiment is actually like. Is there a constant error, regardless of treatment, due e.g. to counting cells? Is the error due to some inherent distribution of, for example, cell masses, so that if one multiplies all the masses by some (ideal, constant) factor due to the treatment, the standard deviation of the total mass also increases by that factor? Etc. I picked the latter, for reasons that made sense to me 8 months ago based on what was done in the talk that inspired the post. One could certainly imagine other possibilities, and it may be useful to play with them; I strongly doubt it will alter the point of my post on the dangers of ‘binary’ thinking.
(2) More importantly, the graph, like the experiment, is not a result of “infinite” replicates, but rather a particular instance of e.g. N=10 measurements. So the variances plotted don’t look like they “ideally” should; the “treatments” are from N=10 draws from some distribution, with means and variances that follow the rules I made up. I just plotted one instance (just like the speaker did only one experiment), and so in a different instance the widths of the bars would look different (and perhaps more “normal”).
It’s a really nice post, but I think the graph is distracting from the main point.
What’s confusing is that the post says that the combined group has “the same” noise as the alone groups, but in the data the for the combined group it is much bigger. Yes it could be chance, but when you did the combined group did you take two values sampled from the same distributions as the #1 and #2 groups and multiply them? Or did you take 10 values from a distribution with mean of 4 and standard deviation of .75? Your boxes in the graph makes it seem like the former but the horizontal arrows make it seem like the latter (the larger standard error for the combined group isn’t reflected).
The example (especially as excerpted here–I think the full post is more clear) is also confusing because 2 is confusing 2*2 = 2+2. Also with s= .75, n = 10 the standard error is .24 I think I would choose means that were closer to each other. On that scale comparing samples from populations with means of 1 and 2 are pretty likely to give you a p value < .05.
Of course the whole point is not to be binary anyway.
Elin — the latter; the “combined” treatment group is a draw of ten new values from a distribution of mean 4. However: looking back at this, there’s an error in what I wrote describing the simulated graphs. The standard deviations of the distributions are 0.75 for the control and 2*0.75 for each sole treatment and 2*2*0.75 for the combined treatment, i.e. imagining a system for which if one multiplies all the measurements (e.g. cell masses) masses by some factor because of the treatment, the standard deviation of the total mass also increases by that factor. (One could of course imagine other sorts of systems.) This doesn’t change the point of the post, as you note. I will correct the text in a moment. (It’s hard to exactly remember what I was thinking 7 months ago, but I’m pretty sure, looking at my notes, that what’s written here is correct!)
You’re definitely right that, in retrospect, I should have chosen factors other than 2, since 2+2 = 2*2 .
Without trying to justify anything about this techniques or to dispute anything Raghu elegantly demonstrates, at least under his hypothesis the two treatments are at least additive… that’s valuable information. If they worked on the same pathway they wouldn’t even be additive. And ideed, in Raghu’s example they are directly additive… So we actually do have some valuable information here amongst the noise, even though the p value demonstration of it is nonsense.
Not just additive, but completely mutually independent.
But I’m puzzled by the negative growth of the controls … basically count me in for no treatment if I have a tumor.
“But I’m puzzled by the negative growth of the controls”
Well, first of all, the graph shows made-up data. So nothing to talk about there.
But, more generally, some cancerous tumors do shrink spontaneously; some even spontaneously disappear. On top of that, even when dealing with genuinely agressive tumors, there is measurement error to consider. “Measuring” growth of a tumor actually means measuring tumor size at two points in time and then differencing them. Each of those two measurements is subject to error. Depending on the method used, the error can be very lage. For example, when “tumor volume” is estimated using x-rays, they measure “diameters” in three directions and multiply them. But tumors are rarely perfectly spherical, and the assessment of just where the “diameter” is can be dicey. On top of that, x-ray films have a certain degree of random magnification (or compression) depending on patient positioning, etc. That’s just the beginning of the measurement error story.
Conventionally, in cancer clinical trials, a tumor is considered to be unchanged in volume unless two consecutive volume estimates differ by more than 25%–that’s how noisy such data are.
Wow!
Thanks, Clyde, for the dose of reality.
This sort of implicit measurement error (noise) is common in clinical data, less so in animal & laboratory studies where many sources of variation are controllable. This is one reason I get a bit frustrated with investigators who want to make a big deal about R^2 variance explained — often low R^2 is saying more about the implicit noise in the measurement than any lack of validity of the relationship. There is a subset of investigators who have been told that R^2 below .8 isn’t believable — often they are reviewers who ask to see the statistic reported, and reject if they don’t like the number, less often as investigators who won’t even try to publish a result with a value below .8. I prefer not to report the statistic.
Wow from me too!
But I was just observing that the whole set up of the story doesn’t really make sense; it would if the control results and the combined results were flipped or if the scale was “shrinkage” rather than “growth”. At least it was just a hypothetical
Yes! In the talk that inspired the post also, there was certainly important information about interactions, mechanisms, etc., there in the data. It would have been great if the speaker focused on these, and made meaningful inferences about interactions, instead of pushing hard to make a “sexy” conclusion.
Jonathan (another one), you are making a common mistake. Two agents acting on the same pathway can have additive effects –or even super-additive effects– where the dose-response relationship is steeper than unity. If you do not characterise the dose-response relationship then it is not possible to determine the presence or absence of “interaction” between two drugs.
Fair enough, although I wasn’t really talking about a dose-response relationship. All I was saying (and in this I still think I’m right) that if the two drugs work along exactly the same pathway, then the tumors that both drugs are effective on subtract from additivity. Thus, where you have Drug A effective (on its own) 40 percent of the time and Drug B effective (on its own) 20 percent of the time and where either drug was effective 10 percent of the time, then you get the combination effective 40 + 20 – 10 = 50, ie less than additive, where additivity only follows if there are no tumors which both drugs shrink.
There must be a graphical way to present your point 1 because it belongs on a t-shirt. People don’t grasp they’re doing dimensional transformations and that they’re assigning or using valuations or gauges which may be relevant in a given volume along specific axial relationships but which often label relatively unconnected sections or which hide substantial dimensional transformation.
“People don’t grasp they’re doing dimensional transformations and that they’re assigning or using valuations or gauges which may be relevant in a given volume along specific axial relationships but which often label relatively unconnected sections or which hide substantial dimensional transformation” wouldn’t fit on a Small
I thought multiplication = one form of interaction? No interaction would mean additive effects?
Yes, it is conventional to assume that a synergistic interaction between drugs will lead to a ‘super-additive’ combined effect. Multiplicative interactions are assumed to be a common class of ‘super-additive’ combination. However, the multiplication should be assessed along the dose axis rather than the response axis as dose-response curves are non-linear and response systems frequently have maxima that cannot be increased. For example, a tumour volume cannot be reduced below 0 and so the tumour reduction scale has a hard-wired maximum of 100% that means that the combined effect of a 80% effective dose of drug 1 with an 80% effective dose of drug 2 will necessarily be sub-additive even if the drugs synergise strongly.
Experiments using single doses of drugs are often inadequate for their intended purpose. If that purpose is the assessment of synergy then you should replace the ‘often’ with ‘always’ in the previous sentence.
That helps!
This example would be better if the effects were actually additive, not multiplicative.
+1
When Rome burnt, in 64 AD, there were no fiddle…
We’ve got fiddles now though!
Hey-diddle-daras, Nero’s citharas, p-values oh-five and below,
don’t prove a jot, so Andrew thought, noshing a ham on wry without mayo.
Andrew’s point number 1 is false. Given that P-values are indices of the evidence in the data against the null hypothesis, they retain their full meaning whether the null hypothesis is true or not.
Michael:
We could do this forever, but . . . My point number 1 is true. Just to clarify, you write, “they retain their full meaning whether the null hypothesis is true or not.” The null hypothesis is false, we already know that. What I wrote was, “In settings where the null hypothesis is not a live option, the p-value does not map to anything relevant.” In just about all the problems I’ve seen, the null hypothesis is not a live option. For example, we can all agree that power pose has some effects; where I depart from the power pose promoters is in their claim that these effects are large and repeatable.
Andrew, in the problem presented a null hypothesis of no effect is well and truly live. Your primary numbered complaint seems irrelevant to the context of the post. The most compelling statistical problem (I addressed the experimental design problem in other comments) is that the authors may have assumed that the P values of 0.08 and 0.07 support the null hypothesis.
For your example of the power pose, by the logic that the null hypothesis cannot be exactly true is not very helpful because in the case where you would not be surprised by a positive or negative effect then the boundary between the positive and negative is not only a live point, but an interesting point. (I do not see why a statistical analysis that does not use a prior should be affected by your opinion that the power pose “has _some_ effects”.)
Michael:
Nope. Power pose does not have “a positive or negative effect.” The effect of power pose depends on the person and situation. It’s sometimes positive and sometimes negative. That’s life.
And the effect of a drug on tumor size could plausibly depend on dosage relative to size of tumor (or of patient), other characteristics of the tumor and/or the individual in which it is situated and/or other events that occur before, during, or shortly after administration of the drug. It could plausibly in some instances be positive and in others negative.
… and thus the population mean can be zero. That is to say, with a statistical model dealing with the population mean, that the null hypothesis would be true. You seem to be disproving your point.
So your argument is really that the statistical model focussed on the population mean is inappropriate. Is that right? (That would not be the same thing as your point number 1, as far as I can see.)
I’m not just making an argument here, I really cannot join the dots in a manner that makes your point number 1 valid. You are doing something differently from me.
Michael:
No, the population mean is not even defined. But if it were defined, it would not be exactly zero, it would be the average of whatever it’s averaging over. You can’t average a bunch of continuous numbers and get exactly zero. And, beyond this, there’s no reason to be interested in some arbitrary average of effects.
Well, maybe, but it depends on what you mean by “exactly zero”. You certainly can average a bunch of continuous numbers and get exactly zero in the real world where every number is, unavoidably, granular.
If your argument is about the infinitesimally small probability of any particular exact outcome then it is a very uninteresting argument. And it is not an argument that is relevant to your point number 1.
Michael:
I continue to disagree with you. There is neither scientific nor policy interest in the claim that the average of the positive and negative effects of power pose in some undefined population of people and scenarios happens to be very close to zero. This average will depend crucially on what people and what scenarios are included in the population, and these issues are never addressed in any of the literature, which should give a clue that this is not what people are talking about. What they are testing is the hypothesis that power pose has exactly zero effect in all situations (what Rubin calls the “Fisher null hypothesis”), and I think this hypothesis is nonsensical.
Andrew: you might call that the “uniformly null” hypothesis. Though I don’t think we’re really capable of testing it with the data at hand, I do agree that this is probably what people *think* they are studying, and it’s what people are interested in (ie. proving that for essentially everyone there is some good effect of power-posing or whatever), and I agree that it’s certainly wrong, the effect will vary in time for each person, could be positive and negative, and in the case of power pose is probably both small on average, and has uniformly pretty limited magnitude.
Michael Lew says:
“Tom, the fact that you imply Mayo would support the notion that a small P-value in isolation provides a license to publish indicates that you are completely unfamiliar with Mayo’s philosophy.”
Hmm, sounds ad hominem to me… however … I’ve been reading her blog for a few years now. I just responded to the words in this one comment. When I wrote my words, I in no way thought what you claim I must have. In fact, my intent was to suggest that Mayo and Andrew might be talking about slightly different things.
Jonathan (another one) says:
“… And ideed, in Raghu’s example they are directly additive… So we actually do have some valuable information here amongst the noise, even though the p value demonstration of it is nonsense.”
I think what’s relevant here is that a non-statistically-significant result should not be replaced by a zero value. After all, the mean *is* the best estimate of the value (in a least squares sense, anyway). In Raghu’s admirable example, we have two “non-significant” but also non-zero results. If we simply call them zero, we throw away some experimental knowledge and therefore bias the conclusion.
If we are trying to demonstrate that General Relativity is wrong, then yes, we no doubt want a very high standard here – way beyond a “reasonable doubt”. If we want to screen for potentially effective drugs, we’d probably want to say “Drug one – interesting, looks good but needs some verification in case it’s only chance. Same for Drug 2. The fact that the combo seems to be (statistically speaking) effective suggests that *at least one* of them is good.”
If Raghu were to rework his example, I’d suggest using some different numbers so that the product and sum come out different (the way it is now, 2+2 = 2*2, which can confuse us), and making sure of the standard deviation of the two-drug random data. But it wouldn’t really change much. The example is pretty nice as it is.
I am a little confused about the terminology used in this discussion and many other such discussions. I understand the term “noise” to refer to imperfections or errors in the measurement process. Natural variation about a mean is something different. Noise-like models may capture it—but it is a different phenomenon.
A example. I just went up to my kitchen and performed two experiments.
Experiment 1. I used the kitchen scale to weigh a single orange (clementine) 10 times—placing the orange at different places on the scale. Result, 6 measurements of 70 g, 4 measurements of 71 g. So, (based on a very limited set of measurements) I conclude that the noise in the measurement has a mean value in the ballpark of 0.5 g with an SD of about 0.5. There is also some quantization noise floating around here (the scale only resolves to 1 g) with SD of about 0.3. But, let’s ignore that.
Experiment 2. I used the same scale to weigh 5 different oranges (not including the 70 g orange). I got 85, 95, 78, 72, and 80 g for the five measurements. The SD of these measurements is 8.6. But, 8.6 is not the SD of the measurement noise—that seems to be less than 1. Rather 8.6 is some statistic about (a) the biology of clementine oranges and (2) the sorting and packaging process used by the wholesaler.
It seems to me that referring to unknown sources of variation as noise risks creating confusion. Am I the only person who is troubled by this use of language?
Bob
Bob:
“Noise” is not a well defined term. As you indicate, it is used to describe some aspect of variation. What aspects of variation are called “noise” depends on how you think of the problem. One reason I like to work with generative models (“Bayesian inference”) is because this forces some clarity on different sources of variation.
Well, you may be right. However, I suspect insisting that “noise” is not well defined might hamper one majoring in Course VI. See https://goo.gl/YZMJ7r or https://goo.gl/0cP5tA.
I do feel that defining a hierarchical model in Stan makes it likely that an analyst will distinguish between natural variations of the quantity of interest and phenomena that distort the measurement of that quantity (noise). In contrast, perhaps why I brought this up, common NHST does not seem to me to make such a distinction.
Bob.
It’s not so much “insisting that “noise” is not well defined” as acknowledging that different people/areas of application use the word differently. If I had my druthers, “noise” would be restricted to things like measurement error (i.e., to what is sometimes called “epistemic uncertainty”), but I realize that it’s nigh on impossible to eliminate a usage that is standard in many fields.
> distinguish between natural variations of the quantity of interest and phenomena that distort the measurement of that quantity (noise)
A very old distinction that perhaps needs more emphasis today.
(some historical links here http://www.stat.columbia.edu/~gelman/research/unpublished/amalgamating4.pdf)
I do think hierarchical modelling challenges one to be more thoughtful about many things.
> common NHST
Most classical statistics were developed to evade important distinctions (i.e. render them not that critical) in circumscribed applications by very bright mathematicians – unfortunately they were seldom clear about that!
(Fisher’s null, Neyman’s null, additive effects, common variances, common intercepts, etc., etc.)
I looked at some of the references in the link above. Thanks. I am enjoying reading the Airy piece but I doubt if I will read all of the references.
Bob.
We do give a very brief summary in the paper.
If I used common sense I would probably have read your piece first—I do intend to read it. But, because I was reading about various topics in optics last week, I was struck by the reference to a work by Airy and I chose to look at it and have kept with it.
Bob
Just a word of caution about the arrogance of statisticians. Or at least, a case of my arrogance.
As a biostatistician, I had an important lesson similar to this one. A researcher came to me and said “I think A by itself should not have an effect, neither should be B, but A+B should. Could you test this so I can put some p-values in my paper?”. Looking at the data, this was the trend you saw, but it felt very cherry picked to me (they also asked for something like 20 other tests to be run). My impression was that they saw this trend, post-hoc pretended that it was what they wanted to see, and asked me for the power to publish it. I fired back “hey, I don’t do cherry picked analyses”. There was tension.
But I didn’t leave the study. As I became more involved, I realized that there was VERY good scientific reason for this interaction effect with a lack of main effects hypothesis to be true that had nothing to do with the data they gave me to. In the way that they presented the analyses to be done, I would say that they didn’t quite have a firm understanding of good statistical practices. But the more I learned about the study, the more I realized that they had a very good understanding of proper scientific processes, and were not just p-hunting for a publication. My ignorance about “non-statisticians are abusing statistics to get publications” actually meant that I was discarding good prior information. My prior about the quality of their priors was wrong.
After awhile, I issued an extremely awkward “sorry for the cherry picking comment”.
Is that what happened in the study discussed in this blog? I certainly do not have enough information to conclude “yes”. But if we are too quick to conclude “you’re not a statistician, so you’re just abusing p-values to get something”, we might be missing out on good scientific research, even if it’s masked behind bad/confused statistical practices.
You make a good point Cliff. The most telling weakness in the example is the inadequacy of a single dose study for testing scientific hypotheses about drug synergy, as I point out in a couple of comments above. The fact that the interpretation of the statistical test of the statistical null hypotheses is flawed is a secondary issue and the role of the P-values in the overall failure is minor.
+1 to Cliff.
CliffAB: I’d love to have a cite of the paper because I’m looking for cases of exactly this, an expected interaction but no expected simple effects.
No reference, but the case involved a couple of biophysics researchers when I was collaborating with a local stats dept chair. We checked for an interaction, thinking we were doing due diligence checking assumptions and we found out when discussing that with them they were only interested in the interaction – the main effects were known and not of interest.
Had we not checked for an interaction, we likely would have never have been aware of that – they were surprised to find out they needed to tell us that.
I withdrew from the project as the stats dept chair over-ruled my concerns about dependencies in the gene expression data arguing that biological dependence does not imply statistical dependence (which admittedly only occurs with probability 1 or something close to 1.)
CliffAB: if this study is published can you give me the cite. I’m looking for examples of an expected interaction effect but no expected single effects.
Sure, but the actual “0 marginals effects with positive interactions” is buried deep.
The paper is:
Expression of A152T human tau causes age‐dependent neuronal dysfunction and loss in transgenic mice
See figure 11. Basically, you want to compare the effect of Dox between figures A and B. Note that Dox appears to do nothing except in the case of the triple-transgenic mice. To me, at first glance it seemed like extreme cherry-picking…until you understand that the science dictates that behavior.
You’ll note that I’m thanked, but not listed as an author. The cherry-picking comment may have been responsible for that one…
Thanks. I tried to google it but started with authorship and quit before googling acknowledgments!
Assume it is safe to receive treatments A and B together and assume also the normality for their effects, say X and Y, as in the simulation. That is, X~N(2,0.75) and Y~N(2,0.75).
Then, what is standard deviation of X+Y (additive effect)? What is the standard deviation of X*Y (multiplicative effect)? A standard deviation of 0.75 for X+Y (or X*Y) seem unreasonable. Theoretically, we can always play with the co-variance between X and Y to get a standard deviation of 0.75.
It’s obvious if the standard deviation of X+Y (or X*Y) remains to be 0.75, the resulting p-value would be smaller as explained in the post because expect a larger sample mean effect due to the combined treatment. However, is such simulation not un-representative? I am skeptical about this claim.
Am I missing something?
Cliff AB,
I simply don’t see how one can ask to test whether the combined treatment A+B has a significant effect if the combined treatment is not applied to real patients? It felt like fabricating data to me. :)
JH:
From this post, I really don’t think there’s enough information to decide whether everything’s based on flawed logic or not (unless there’s some link to the real paper I missed). First off, that’s the actual data the original researcher presented. Second, we don’t know the background behind why it was decided that the interaction should be stronger.
I will definitively say that if the above data was ALL they had and that’s what lead them to the conclusion, then that’s easily interpreted as the confusion of p-values leading to very bad conclusions.
But now consider another scenario. I’m not saying I know the researcher started the study with the following information, but let’s just pretend they do. The biology tells us that treatment A has molecules that are extremely likely to bind with cancerous cells. Treatment B has molecules that will destroy cells in which A appears. In this scenario, we would expect near 0 effects of A and B alone, but strong effects of A + B. And with regards to standard deviations of the response variable “tumor sizes”, we should expect A and B (alone) to have about the same standard deviation…but A + B should have much smaller standard deviation (although a log transform may fix that)!
IF that were our background, and we saw that A + B was statistically significant, A, B alone were not, and (A) + (B) less than (A+B) (i.e. interactive effects greater than individual effects) I would say the data supported the researcher’s hypotheses. I would have a lot of faith that the A + B effect was real, and would say this supports the idea that (A) + (B) less than (A+B). We might want to do a formal test to address the strength of the evidence of (A) + (B) less than (A+B).
On the other hand, if a priori they had no idea about the molecular effects of A, B and they hypothesized (A+B) greater than (A) + (B) after seeing results, my posterior would look a whole lot like my prior.
(Also not quite sure why you say (A+B) was not applied to real patients? In both my example, and the example in Andrew’s post, it seemed that (A+B) was applied to real patients. Well, in my case, the “patients” were mice. If those mice were patients, they should really consider switching care providers).
Agh. That should read:
“…that’s NOT the actual data the researcher provided…”
JH says:
“Then, what is standard deviation of X+Y (additive effect)? What is the standard deviation of X*Y (multiplicative effect)? A standard deviation of 0.75 for X+Y (or X*Y) seem unreasonable.”
This is well-known. For X+Y, var(X+Y) = var(X) + var(Y). For XY, it’s var(XY)/(XY)^2 = var(X)/X^2 + var(Y)/Y^2. Of course, that’s when X and Y actually have independent errors.
There are more ways treatments can effect variances (and higher moments) than in your philosophy (math) above.
It is an empirical question, not distribution theory – right?