A couple people pointed me to this article, “The Moral Hazard of Lifesaving Innovations: Naloxone Access, Opioid Abuse, and Crime,” by Jennifer Doleac and Anita Mukherjee, which begins:
The United States is experiencing an epidemic of opioid abuse. In response, many states have increased access to Naloxone, a drug that can save lives when administered during an overdose. However, Naloxone access may unintentionally increase opioid abuse through two channels: (1) saving the lives of active drug users, who survive to continue abusing opioids, and (2) reducing the risk of death per use, thereby making riskier opioid use more appealing. . . . We exploit the staggered timing of Naloxone access laws to estimate the total effects of these laws. We find that broadening Naloxone access led to more opioid-related emergency room visits and more opioid-related theft, with no reduction in opioid-related mortality. . . . We also find suggestive evidence that broadening Naloxone access increased the use of fentanyl, a particularly potent opioid. . . .
I see three warning signs in the above abstract:
1. The bank-shot reasoning by which it’s argued that a lifesaving drug can actually make things worse. It could be, but I’m generally suspicious of arguments in which the second-order effect is more important than the first-order effect. This general issue has come up before.
2. The unintended-consequences thing, which often raises my hackles. In this case, “saving the lives of active drug users” is a plus, not a minus, right? And I assume it’s an anticipated and desired effect of the law. So it just seems wrong to call this “unintentional.”
3. Picking and choosing of results. For example, “more opioid-related emergency room visits and more opioid-related theft, with no reduction in opioid-related mortality,” but then, “We find the most detrimental effects in the Midwest, including a 14% increase in opioid-related mortality in that region.” If there’s no reduction in opioid-related mortality nationwide, but an increase in the midwest, then there should be a decrease somewhere else, no?
I find it helpful when evaluating this sort of research to go back to the data. In this case the data are at the state-year level (although some of the state-level data seems to come from cities, for reasons that I don’t fully understand.) The treatment is at the state-month level, when a state implements a law that broadens Naloxone access. This appears to have happened in 39 states between 2013 and 2015, so we have N=39 cases. So I guess what I want to see, for each outcome, are a bunch of time series plots showing the data in all 50 states.
We don’t quite get that but we do get some summaries, for example:
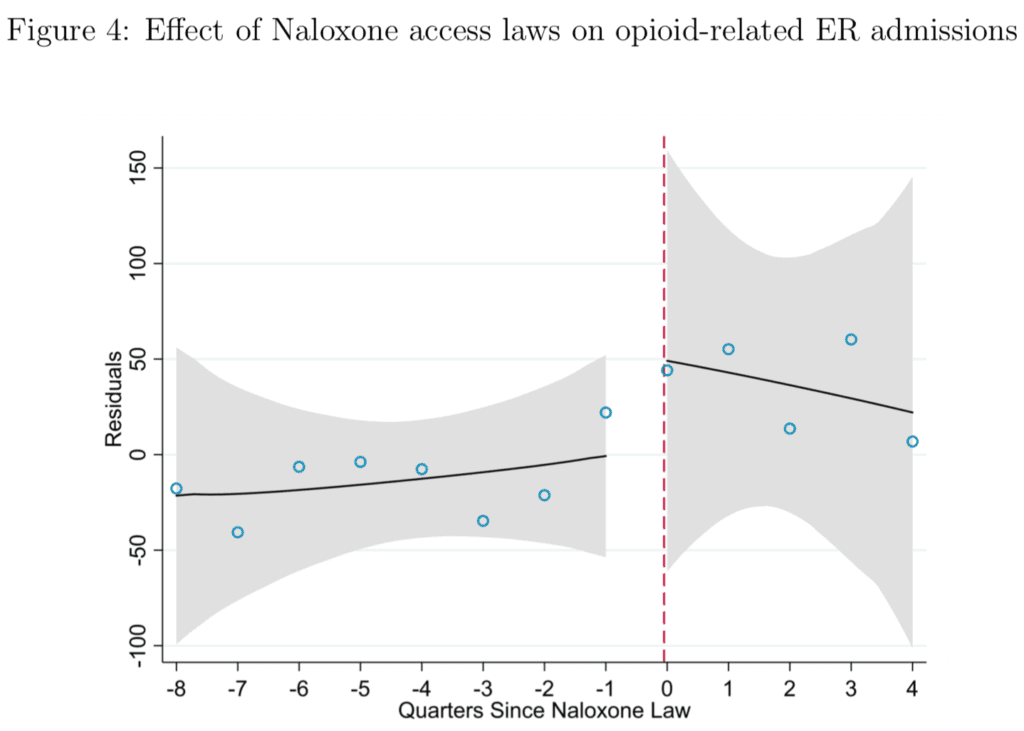

The weird curvy lines are clearly the result of overfitting some sort of non-regularized curves; see here for more discussion of this issue. More to the point, if you take away the lines and the gray bands, I don’t see any patterns at all! Figure 4 just looks like a general positive trend, and figure 8 doesn’t look like anything at all. The discontinuity in the midwest is the big thing—this is the 14% increase mentioned in the abstract to the paper—but, just looking at the dots, I don’t see it.
I’m not saying the conclusions in the linked paper are wrong, but I don’t find the empirical results very compelling, especially given that they’re looking at changes over time, in a dataset where there may well be serious time trends.
On the particular issue of Nalaxone, one of my correspondents passes along a reaction from an addiction specialist whose “priors are exceedingly skeptical of this finding (it implies addicts think carefully about Naloxone ‘insurance’ before overdosing, or something).” My correspondent also writes:
Another colleague, who is pre-tenure, requested that I anonymize the message below, which increases my dismay over the whole situation. Somehow both sides have distracted from the paper’s quality by shifting the discussion to the tenor of the discourse, which gives the paper’s analytics a pass.
There’s an Atlantic article on the episode.
Of course there was an overreaction by the harm reduction folks, but if you spend 5 minutes talking to non-researchers in that community, you’d realize how much they are up against and why these econ papers are so troubling.
My main problem remains that their diff-in-diff has all the hallmarks of problematic pre-trends and yet this very basic point has escaped the discussion somehow.
There is a problem that researchers often think that an “identification strategy” (whether it be randomization, or instrumental variables, or regression discontinuity, or difference in difference) gives them watertight inference. An extreme example is discussed here. An amusing example of econ-centrism comes from this quote in the Atlantic article:
“Public-health people believe things that are not randomized are correlative,” says Craig Garthwaite, a health economist at Northwestern University. “But [economists] have developed tools to make causal claims from nonrandomized data.”
It’s not really about economics: causal inference from observational data comes up all the time in other social sciences and also in public health research.
Olga Khazan, the author of the Atlantic article, points out that much of the discussion of the paper has occurred on twitter. I hate twitter; it’s a medium that seems so well suited for thoughtless sloganeering. From one side, you have people emptily saying, “Submit it for peer review and I’ll read what comes from it”—as if peer review is so great. On the other side, you get replies like “This paper uses causal inference, my dude”—not seeming to recognize that ultimately this is an observational analysis and the causal inference doesn’t come for free. I’m not saying blogs are perfect, and you don’t have to tell me about problems with the peer review process. But twitter can bring out the worst in people.
P.S. One more thing: I wish the data were available. It would be easy, right? Just some ascii files with all the data, along with code for whatever models they fit and computations they performed. This comes up all the time, for almost every example we look at. It’s certainly not a problem specific to this particular paper; indeed, in my own work, too, our data are often not so easily accessible. It’s just a bad habit we all fall into, of not sharing our data. We—that is, social scientists in general, including me—should do a better job of this. If a topic is important enough that it merits media attention, if the work could perhaps affect policy, then the data should be available for all to see.
P.P.S. See also this news article by Alex Gertner that expresses skepticism regarding the above paper.
P.P.P.S. Richard Border writes:
After reading your post, I was overly curious how sensitive those discontinuous regression plots were and I extracted the data to check it out. Results are here in case you or your readers are interested.
P.P.P.P.S. One of the authors of the article under discussion has responded, but without details; see here.
Did I read that abstract correctly?
Just let them die? Definitely cheaper.
I am pretty sure I do not want to meet the authors.
Jkrideau:
I think they’re just stating the results of their model; they’re not saying that letting people die is a better outcome. This relates to my point above that “saving the lives of active drug users” is an intended, not unintended aspect of the law. So I disagree with some of their framework, but I don’t think it’s fair to say that the authors think that “just let them die” is a good plan.
From the end of the paper:
“Our findings do not necessarily imply that we should stop making Naloxone available to
individuals suffering from opioid addiction, or those who are at risk of overdose. They do
imply that the public health community should acknowledge and prepare for the behavioral
effects we find here. Our results show that broad Naloxone access may be limited in its
ability to reduce the epidemic’s death toll because not only does it not address the root
causes of addiction, but it may exacerbate them.”
A charitable interpretation of (1): The intent is to save their lives, but it is unintended that by saving their lives they continue to abuse. I take (1) as just saying drug abuse rates are likely to be higher if the mortality rate of addicts are lower (though I have no idea how quantitatively important it is). Its kind of silly, but as baseline I would think it would be important to take into account (its a sample type of composition issue) if you are really interested in measuring (2), which is the incentive effect of lower risk of abuse, a clearer example of moral hazard here. I could plausibly see an increase in some amount of abuse, but I wouldn’t expect measure risk the most pertinent factor in the the choice to abuse. On the mortality side though I am skeptical, I like how you put it in terms of first and second order effects.
The abstract doesn’t even say that “saving the lives of active drug users” is an unintentional effect. It says that “Naloxone access may unintentionally increase opioid abuse”.
“Saving the lives of active drug users, who survive to continue abusing opioids” is clearly listed as one of the possible mechanisms that may lead to that unintended consequence (the increase in opioid abuse).
> If a topic is important enough that it merits media attention
Really? Media attention is now indicative of the importance of a topic?
Carlos:
s/media attention/media attention or policy relevance/
Sure, I agree that when an important topic deserves media attention making more data available it’s important. On the other hand, most public discussions won’t even fully take into account the data which is already available!
I’m also confused about the comment (not yours) “it implies addicts think carefully about Naloxone ‘insurance’ before overdosing, or something”. I don’t know if your correspondent is equally skeptical of all the “risk compensation” studies or thinks that in other cases individuals may think carefully abour the level of risk they are willing to take.
It’s pretty sneaky to make these graphs look like a regression discontinuity design when the line to the left of the threshold are just uncontrolled for pre-trends.
Not going to read the paper, but I don’t understand their logical model. Staggered implementation reflects different stages of the underlying condition, if we treat the ‘epidemic’ as a condition that expresses over the space of the US, how do you remove the effects of growth in the underlying waveform? Second, naxolone isn’t ‘available’ as much as it’s ‘used’. Ibuprofen is available. You have a bottle at home. Narcam is usually administered by an EMT, cop or firefighter, maybe at an ER, rarely because you have an injector lying around like a bottle of Tylenol just in case someone you know ingests fentanyl. Third, I remember learning how to use the injector: it wasn’t long ago, and one had never been used in our town of nearly 60,000 people – with one used in the next suburb, which is a city, in 6 months. By the time training was over, meaning within several weeks, it had been used 3 or 4 times in town and there’d been a rapid increase in usage everywhere around. (Odd epidemic: started in more rural areas, sort of like crystal meth did, and then moved into the suburbs. Downer epidemics have typically started in cities and moved out, and then ended with a rash of deaths. These new epidemics come from the other direction and have more staying power. Don’t know why.) I cant’t get past the logical model issues – and there are more off the top of my head – to think about the analysis. To me, that’s a big problem. Take the new paper about gaming not causing aggression. They tested 77 people. If the effect were large, given the number of gamers, there’d be large numbers of obviously affected people. But they’re testing 77 people, which says right off the bat the effects aren’t that large because they’re arguing whether we see anything when we have hundreds of millions of test subjects. 77 people isn’t enough to find anything when the n is in the gazillions, especially if you model a spectrum in which there are mass killers at one end and angry but impotent dudes at the other. Is the idea to identify rage that can become real? If so, then 77 doesn’t get close except by freak luck. I can’t think of an effect you could reliably estimate from 77 people. Even if all 77 showed rage symptoms that doesn’t say anything reliable beyond: alert, check this out some more!
“But twitter can bring out the worst in people.”
This was hilarious in response to unsophisticated critiques of a research study given all the nazis and harrassment on twitter. Not sure if you were intentionally playing into your character here or if it was a completely genuine comment or both, but funny all ways.
“Public-health people believe things that are not randomized are correlative,” says Craig Garthwaite, a health economist at Northwestern University. “But [economists] have developed tools to make causal claims from nonrandomized data.”
I’m so tired of public health bashing by economists. I’ve been reading this book “Expecting Better” about pregnancy by Emily Oster, and it’s chock full of it. Have they never heard of Jamie Robins, the public health guy who formalized and developed causal inference for time varying treatments? (many) Economists both take too much credit for causal inference and are overconfident in their preferred approaches.
Hey – economist here.
Not trolling, but I honestly had not heard of James Robins. That’s on me, though I don’t know how many people in most disciplines read widely outside of them.
Now that I know what name to look for I see that he’s cited in Wooldridge and in Mostly Harmless, to take two examples from my shelf.
All of this is to say that the answer to your question is probably “No, some of them may not have heard of him.” But now I have and I’ll check out more.
The stuff I read in medical journals (which overlaps somewhat with my own work) generally doesn’t involve any attempt at causal inference.
And on the present study… my sense from the graphs is that they find nothing, despite achieving some statistical significance threshold.
I swore that no one on social media was gonna turn me into a harpie. I actually find all the politics and swarmy comments pretty intriguing. It just gives me material for a script.
On Twitter I follow some of the people who comment here because I perceive them to be good writers prone to good insights. From my repeated observations that invariably sober authors of closely argued positions here (as well as in their published papers) sometimes become flingers of logical fallacies and nasty retorts there, I have infered that Twitter brings out the Hyde in Drs. Jekyll.
I’m with andrew. I hate Twitter and refuse to use it. I also hate Facebook for anything political but I use it to keep up with what friends in distant parts of the country are up to… It just makes people turn off their brain when it comes to policy etc. The only people i will argue with on FB are the two pros i know, PhDs in philosophy
Maybe also a lawyer i know who does public health related stuff. I’m appalled at what little my educated friends in science etc know about formulating and engaging logical argument.
I love twitter. For us layman it opens up a world of experts and different viewpoints etc It just takes some time to seperate the wheat from the chaff and to train yourself not to troll people.
When I first saw these plots, I didn’t notice the y-axis label…these are all residual plots. Should they look like random data if their model is good?
Good catch, I hadn’t noticed that. Now I’ve downloaded the paper and have many complaints to add to Andrew’s from above. First, why does it have to be so hard to read these papers? I’m growing weary of having these long papers with all the figures and tables at the end of the paper. I know journals ask for things this way, but I think papers posted for public consumption should put it in an order that can be read – otherwise I have a strong impression the intent is not to really have any one understand it.
Second, let’s look at Figure 4 above as an example. The description in the paper is that these are the residuals for a 5 year period for every metro area in the US – 20,000+ data points. So, what am I looking at in this figure? Doesn’t look like a residual plot I would expect. I’ll figure it out eventually, but at this point it just gives me a headache.
Do these effect estimates really mean anything if the model isn’t “correctly specified” anyway? Eg, this was news to me:
http://statmodeling.stat.columbia.edu/2018/03/15/need-16-times-sample-size-estimate-interaction-estimate-main-effect/#comment-685867
tldr: You can get totally different primary outcome effects simply by coding some “control variable” like male/female as 0/1 instead of 1/0. The difference was enough to alter power from ~70% to ~30% in that example.
For table 2 it says:
Assuming “Good Samaritan laws” is binary, did they code having such laws as a one, or not having the laws as one? This could (I have no idea if it does) apparently substantially change the final estimate for nalaxone laws.
I think in that case it wasn’t switching from 0/1 to 1/0 (that can’t do anything) it was switching from 0/1 to -1/1 so that your intercept estimates the average between the two and the coefficient estimates the difference from the average.
The average between the two can then be estimated with precision, but the difference between the two becomes imprecise. With 0/1 the main effect is confused with the sex interaction.
Take all of that with a grain of salt, because I didn’t look into that comment carefully, I just know that there’s some confusing stuff that happens with classical “contrasts” that doesn’t happen in doing Stan models because you aren’t confounding two concepts: estimation with modeling. The model is the model, and estimation is just a carefully coded general purpose mechanical solution of an HMC differential equation.
Yes it does. I modified this from what I pasted in that other thread to use 1/0 instead of M/F (btw when I tried to copy-paste-run the code from there I had to replace the minus sign and all quotes…): https://pastebin.com/J79eNNKd
Here are the results:
So either there is a very bad bug in R’s lm function or these “effect size” estimates depend on arbitrary choices of the researcher. Like you I don’t do analyses like this to begin with (it is wrong anyway for other reasons), but many people do.
Try using looking at predictions. You’ll notice they are exactly identical. And of course the “main effects” change, because you’ve redefined what the baseline/interaction groups are.
The exact same thing would happen in Stan, for what it’s worth.
Yep, the predictions are the same but people don’t only use these for the predictions (anyway you would use some ML technique these days for that) they use them to get some estimate of the effect. Regarding “of course”, here is what I said in the other thread:
This is exactly why some old-school statisticians (Nelder, Venables, etc.) spent so much time yelling about the “principle of marginality”, i.e. that one shouldn’t try to test main effects in the presence of interactions. Such effects *can* be tested, but their meaning and value depends entirely on the contrasts/coding of the main effects.
In Stan you typically understand more about the model you are specifying because you build it up from the ground using actual math.
You’re right here that the issue is that the meaning of the coefficients changes because the model is specified in terms of a baseline and a perturbation and the baseline changed so the perturbation changed to keep the prediction constant.
To contrast what is going on here with what typically would be going on in Stan, I’d probably write this in stan as two totally separate regressions, in pseudocode:
MaleVals ~ normal(MaleBaseline + MaleGroupEffect,…)
FemaleVals ~ normal(FemaleBaseline + FemaleGroupEffect,…)
And so, no the confusion wouldn’t happen at all. In the end if you wanted to understand the “sex effect” you’d look at differences in the posterior samples between the male parameters and the female parameters.
Daniel:
If you extracted the same estimates that you’re looking at in your Stan example from an lm object, the issue would be resolved in the exact same manner.
The number of people who know how to run lm is far higher than the number who know how to extract the relevant alternative parameterization estimates. Lm exists precisely to hide details like this for “ease of use”
Dale said, “why does it have to be so hard to read these papers? I’m growing weary of having these long papers with all the figures and tables at the end of the paper. I know journals ask for things this way, but I think papers posted for public consumption should put it in an order that can be read – otherwise I have a strong impression the intent is not to really have any one understand it.”
+1
I am surprised the authors of the paper did not expect the intensity of scrutiny; after all, they were making strong counterintuitive claims about a deeply relevant subject.I came across another skeptical evaluation of this paper here
https://www.healthaffairs.org/do/10.1377/hblog20180316.599095/full/
And a more favorable response that references this paper
https://academic.oup.com/qje/article-abstract/121/3/1063/1917864
which models potential moral hazards associated with HIV treatment breakthroughs and increase in risky behavior. That causal identification is difficult and problematic is not emphasized enough in news media versions of important academic papers.
I also followed some twitter threads accusing critiques as indicative of *mansplaining* and sexism. And pretty soon, the Atlantic article made it an issue. As a researcher, I understand the changing cultural norms of the academic community and I sincerely look for ways in to make scientific debates only about the the results and the science and not about the people involved. But it is extremely frustrating to see an increasing moralization and politicization of scientific critiques. I have seen accusatory attacks on blogs like Data Colada and this one in various media outlets that seem very unfair and almost clickbait-ish.
I found similar bad account of a recent Chetty and Hendren article on demographic differences in social mobility. Although the authors’ executive summary
http://www.equality-of-opportunity.org/assets/documents/race_summary.pdf
and the paper
http://www.equality-of-opportunity.org/assets/documents/race_paper.pdf
contain just a single written instance of the word _causal_ and do not use any morally value laden words, the NYTimes article
https://www.nytimes.com/interactive/2018/03/19/upshot/race-class-white-and-black-men.html
contains copious amounts of causal narratives and makes extensive use of morally colored terminology. It is my suspicion that such moral coloring obfuscate scientific and academic debates.
Compulsory XKCD strip to go with this paper: https://www.xkcd.com/1725/
Partially tangential comment, not really about the paper under discussion here.
In one sense, I hope that the authors’ conclusions are correct. The public discussion of the opioid epidemic is driven by the mortality effects. But deaths from opioid addiction are only the tip of the iceberg. Before dying, every addict destroys his or her life. They put themselves at risk of serious chronic diseases like HIV and hepatitis C if they are injecting. They are often driven to theft to support their habits. They can end up incarcerated. They also inflict havoc on the lives of others, particularly their family members, as a result of loss of income, increased dependency, neglect of responsibilities, theft from household members, endless lying and manipulation bringing unsavory others into the environment.
Opioid addiction is a disease whose misery is difficult to imagine for those who have not directly experienced or witnessed it. Death is often perceived as a relief by the addict, and even more often by those who are personally connected to the addict. The death from overdose affects one person in minutes. The misery of one addict’s addiction afflicts the addict and everyone in his or her life for years on end, with repercussions sometimes extending beyond the addict’s demise. Call these second order effects if you like, but they are massive and it would not be unreasonable to think of them as dwarfing the mortality impact overall.
If the result of a study like this is that more attention is placed on these other effects of opioid addiction, with a view to mitigating them somehow, that will be a good thing. And that is something that naloxone cannot possibly do.
+1
I only partially agree. Naloxone isn’t “the answer,” but only a temporary fix — until we develop effective methods of getting people off opioids, and stop the over-prescription of opioids
These graphs look like someone hit the LOESS button on some package. I never heard of D of D till a few weeks ago. It seems very simplistic.
I went to a very good talk at the JSM 2014 about suicide. Suicide has a geometric distribution–a sequence of attempts followed by the event of death. We can think of overdoses the same way. So if naloxone lowers the probability of death at an event, there will be more overdoses. But in between the overdoses they can take action. Once they are dead, this is no longer possible.
+1 But we also need (as mentioned above) to implement more judicious drug prescription practices (thereby reducing the incidence of addiction), and to develop and implement better ways of treating addiction when it occurs.
Since everyone here seems to hate Twitter, one of the authors expressed this on Twitter in response to Andrew’s post:
“I didn’t find his critique all that compelling. In most of the graphs I think there’s clearly a change in the mean at time zero, and we have a zillion robustness checks that convince us the patterns are real. I also wish the data were less noisy but such is life.”
https://twitter.com/jenniferdoleac/status/976797663231344640
I might not have been convinced by a mere billion robustness checks, but a zillion? I think she might have a point. ;)
Justme:
There are a few problems with that response:
1. “In most of the graphs I think there’s clearly a change in the mean at time zero.” I can go further than that! In all the graphs there’s definitely a change in the mean at time zero. Nothing is ever constant. Attributing observed changes to a particular treatment, that’s another story. In addition the author does not address the problem of the goofy curves.
2. Robustness checks. The usual problem with robustness checks is that they are performed, not to explore, but to bolster or confirm a conclusion already arrived at.
3. The larger issue of researchers responding defensively to criticism. In any particular case, the defensive attitude could be appropriate, but it can’t be right for this attitude to come up almost all the time.
4. Relatedly: I also noticed that another commenter on twitter replied, “I do think providing stronger visual support would strengthen your case.” Not necessarily! If the conclusions are well justified from data, then, sure, stronger visual support would strengthen the case. But if the data analysis is overconfident, then, no, stronger visual support would just make it clear what went wrong. The larger problem is that attitude that the authors of the paper should be “strengthening their case.” We’re scientists, not advocates! Our goal is to get closer to the truth, not to build a case or win an argument.
In any case, I hope the authors of that paper, and others who are interested in the points made in my post above, can post their questions and disagreements here, in comments, where there is space for careful discussion. Again, with a goal of learning and doing better science, I think an open discussion here is much preferable to snippets on twitter.
“The larger problem is that attitude that the authors of the paper should be “strengthening their case.” We’re scientists, not advocates! Our goal is to get closer to the truth, not to build a case or win an argument.”
+1000
My understanding is that the underlying assumption that changes in the law increased Naloxone access is itself not supportable empirically(in a number of cases the law change was to formalise already existing pre law Naloxone use, in other cases distribution didnt increase etc) More broadly, because policy change across states is heterogenous and endogenous(I think) could this be called a natural experiment? (Im not sure if that matters. I queried some people on twitter whether it can be classified as a natural experiment, and it seemed to not be important. But my understanding is a natural experiment often implies a greater weight of causal evidence?)
This new Miguel Hernan article has been echoing a lot of the thoughts here:
http://ajph.aphapublications.org/doi/abs/10.2105/AJPH.2018.304337?af=R
The worst problem about Figure 4 is that half the supposed increase seems to have already happened at t=-1, i.e. three months before the law came into effect…
great post. there’s a definite tendency in the Econ community to torture the data with fancy econometrics when it’s insufficiently conclusive on its own. this is a good reminder that before looking at “a zillion robustness checks” we should look critically at the raw data and ask if it passes the sniff test.