The new rules for D&D 5e (formerly known as D&D Next) are finally here:
D&D 5e introduces a new game mechanic, advantage and disadvantage.
Basic d20 Rules
Usually, players roll a 20-sided die (d20) to resolve everyting from attempts at diplomacy to hitting someone with a sword. Each thing a player tries to do has a difficulty and rolling greater than or equal to the difficulty (with various modifiers for ability and training and magic items) means the character was successful.
Advantage and Disadvantage
As of 5th Edition (5e) rolls can be made with advantage or disadvantage. The rules are:
- Advantage: roll two d20 and take the max
- Normal: roll one d20 and take the result
- Disadvantage: roll two d20 and take the min
So what are the chances that you’ll roll equal to or above given number with advantage, normally, or with disadvantage? Here’s a table.
| roll | disadvantage | normal | advantage |
|---|---|---|---|
| 20 | 0.002 | 0.050 | 0.098 |
| 19 | 0.010 | 0.100 | 0.191 |
| 18 | 0.022 | 0.150 | 0.278 |
| 17 | 0.039 | 0.200 | 0.359 |
| 16 | 0.062 | 0.250 | 0.437 |
| 15 | 0.089 | 0.300 | 0.510 |
| 14 | 0.123 | 0.350 | 0.576 |
| 13 | 0.160 | 0.400 | 0.639 |
| 12 | 0.202 | 0.450 | 0.698 |
| 11 | 0.249 | 0.500 | 0.751 |
| 10 | 0.303 | 0.550 | 0.798 |
| 9 | 0.361 | 0.600 | 0.840 |
| 8 | 0.424 | 0.650 | 0.877 |
| 7 | 0.492 | 0.700 | 0.910 |
| 6 | 0.564 | 0.750 | 0.938 |
| 5 | 0.640 | 0.800 | 0.960 |
| 4 | 0.723 | 0.850 | 0.978 |
| 3 | 0.811 | 0.900 | 0.990 |
| 2 | 0.903 | 0.950 | 0.998 |
| 1 | 1.000 | 1.000 | 1.000 |
The effect is huge. There’s less than a 9% chance of rolling 15 or higher with disadvantage, whereas there’s a 30% chance normally and a 51% chance with advantage.
[Update II: Turns out that The Online Dungeon Master, a blog I read regularly for 4e module reviews and play reports, generated the same table over a year ago (using Excel simulations, no less; a commenter provides a good breakdown of the analytic solution). That’s been the story of my life coming into a new field. I agree that this tabular form is what you want for reference, but the easiest way to understand the effect is looking at the non-linearity in the graph below.]
Here’s a plot (apologies for the poor ggplot2() and png() defaults — I don’t understand ggplot2 config well enough to make titles, clean up labels, axes, tick mark labels, boundaries, margins, colors, and so on to make it more readable without spending all night on the project).
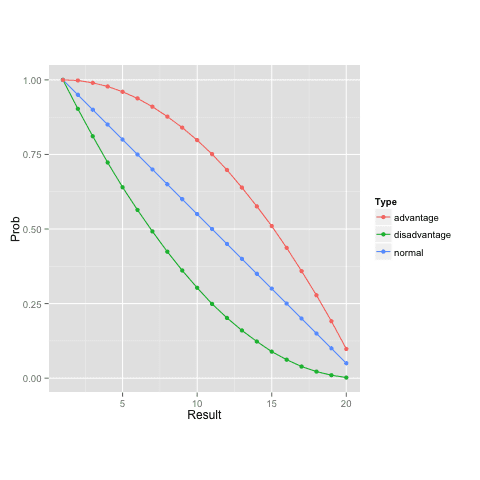
The vertical distances at a given horizontal position show you how much of a bonus you get for advantage or disadvantage.
[Update: There’s an alternative plot on the Roles, Rules, and Rolls blog that displays the difference between advantage and a simple +3 bonus, as used in previous D&D editions.]
Analytic Solution
The probabilities involved are simple rank statistics for two uniform discrete variables.
You can compute these probabilities analytically, as I show in Part III of the page where I explain the math and stats behind my simple baseball simulation game, Little Professor Baseball.
The basic game is a cross between All-Star Baseball and Strat-o-Matic. I wanted a rolling system where both players roll, one for the batter and one for the pitcher, and you use card for the player with the highest roll to resolve the outcome. The winning roll is going to have a distribution like the advantage probabilities above (except that Little Professor Baseball uses rolls from 1–1000 rather than 1–20. As a bonus, earlier sections of the math page explains why Strat-o-Matic cards looks so extreme on their own (unlike the All-Star Baseball spinners).
I developed the game after reading Jim Albert’s most excellent book, Curve Ball, and I included the cards for the 1970 Cinncinnatti Reds and Baltimore Orioles (which for trivia, were mine and Andrew’s favorite teams as kids).
Simulation-Based Calculation
I computed the table with a simple Monte Carlo simulation, the R code for which is as follows.
oneroll <- function(D) {
return(sample(D,1));
}
advantage <- function() {
return(max(oneroll(20), oneroll(20)));
}
disadvantage <- function() {
return(min(oneroll(20), oneroll(20)));
}
NUM_SIMS <- 100000;
advs <- rep(0,NUM_SIMS);
for (n in 1:NUM_SIMS)
advs[n] <- advantage();
disadvs <- rep(0,NUM_SIMS);
for (n in 1:NUM_SIMS)
disadvs[n] <- disadvantage();
print("", quote=FALSE);
print("CCDF (Pr[result >= k])",quote=FALSE);
print(sprintf("%2s %6s %6s %6s", "k", "disadv", "normal", "advant"),
quote=FALSE);
cumulative_disadv <- 0;
cumulative_norm <- 0;
cumulative_adv <- 0;
for (k in 20:1) {
cumulative_disadv <- cumulative_disadv + sum(disadvs == k) / NUM_SIMS;
cumulative_norm <- cumulative_norm + 0.05;
cumulative_adv <- cumulative_adv + sum(advs == k) / NUM_SIMS;
print(sprintf("%2d %6.3f %6.3f %6.3f",
k,
cumulative_disadv, cumulative_norm, cumulative_adv),
quote=FALSE);
}
I'm sure Ben could've written that in two or three lines of R code.
Andrew, I didn’t know you were a gamer!
(j/k Bob)
Surely there is an app for that, one where virtual dice can be weighted so advantage and disadvantage could range from 100 to 0. In the latter case say you seldom roll above a 1. Kind of like the Cossacks charging German panzers on horseback during WWII.
I see the beauty of physically rolling dice. But it seems to come at the expense of very constrained notion of advantage.
PS Moreover, to the extent personas in games largely boil down to conditional probabilities based in skills etc, then allowing for more persona related weighting is like making way for more individual differentiation or #inequality.
I think the motivation of using advantage rather than a straight bonus is the non-linearity that makes the additive bonus smaller at the extremes and greater in the middle. You could intensify the same thing by making N rolls and tking the min or max.
On the other hand, there’s really nothing you can do like advantage if it’s just a single roll other than choose the bonus or difficulty class accordingly.
In the end, D&D is fantasy simulation, not physics simulation. So you just might want to give those Cossacks a fighting chance.
The DMs I play with, myself included, do all sorts of on-the-fly compensation by determining how many ability checks are going to be required to succeed in some task. Instead of just one roll with disadvantage to climb a slippery wall, you might have to make two or more rolls. If either goes wrong, you typically can get a save to recover. So it’s all sorts of nonlinear in play.
For example, I have a weekly game where a friend of mine runs a steampunk fantasy game set in the Napoleonic era. It’s been house-ruled for the last 35 years, starting with the rules from Bushido and Traveler. Here’s how the equivalent of a D&D skill challenge went just last week. The setting is an old dwarven limestone cave in a haunted valley outside of Acre, Egypt, where we’re helping the French army and aeronautical corps scout transport routes for the siege. My Maltese dwarven military engineer had just belayed his necromancer friend’s safety rope, when the necromancer sets out across a narrow ledge over a crevasse and fails his climb roll, starts slipping as the limestone underfoot crumbles away, grabs Wile E Coyote style for a purchase, but fails his save to stabilize himself. He then plunges to the end of the dwarf’s rope, which luckily holds taut. The necromancer is now dangling cave monster bait, and as the dwarf fails his strength roll to pull the struggling necromancer up and the necromancer fails his roll to scrabble up the sheer wall of the crevasse, a giant millipede obligingly snatches him off the end of his rope, leaving the dwarf with a frayed rope end. It’s the dwarf’s last rope, and he’s going to have to free climb down to the millipede’s lair …
If you follow the dev process, the actual reason for the mechanic is that they thought keeping track of all of the situational +X and -Y bonuses in previous editions was too much work and thought this system was simpler.
“Subjecting anyone to a recounting of your D. & D. campaign is worse than boring them with last night’s dreams or your commuting woes” says Jon Michaud of the New Yorker (http://www.newyorker.com/online/blogs/culture/2014/07/dungeons-dragons-saved-my-life.html)
Oops — forgot to add the zombie, which old school gamers such as myself will recognize from way back in the 1970s when the original Monster Manual came out.
Looks like a researcher looking for significant findings.
Having cut my teeth on AD&D 1e, I remember enumerating all possibilities of “4d6 drop lowest” to compare with the expectation of other methods of character generation. Thanks for the memories!
Wondering why you chose 100000 random draws instead of enumerating the 400 possibilities?
disadvantage <- unlist(outer(1:20,1:20, function(x,y) ifelse(x<y,x,y)))
advantage y,x,y)))
Oops. my comment got mangled. The code should have been
disadvantage <- unlist(outer(1:20,1:20, function(x,y) ifelse(x<y,x,y)))
advantage y,x,y)))
I should’ve done that. The only reason I didn’t is that it didn’t even occur to me to enumerate all 400 possibilities (despite, like Avi, having figured out the best 3 of 4d6 solution in high school by brute force).
In the case of the max of two i.i.d. draws from a Uniform(1,K), there’s an analytic solution that’ll work even when K is large. Of course, even K=1000 is easy to enumerate fully.
This looks on the face of it like a massive intervention in the ease with which GMs can run d&d rules. For all its considerable problems, the D&D system is very accessible to GMs because it combines three simple ideas to make difficulty decisions easy: target numbers, uniform distribution, and situational modifiers (the 3rd edition guideline was a standard +2 I think). Adding something like a max/min roll like this completely breaks this intuitive structure, and makes it really hard for GMs to think about how to judge difficulty. By way of comparison, for e.g. the Iron Kingdoms system allows a “boost” which adds 1d6 to skill checks: this is a quantifiable probability improvement that does not fundamentally change the shape of the distribution or its intuitive feel. But taking the max of two rolls is not intuitive and will make it really hard to fiddle with probabilities for a GM.
Personally I loathe the uniform distributions of D&D, and I htink they model a really weird world, but they are at least intuitively understandable, and it’s easy to incorporate situational modifiers (and to design your own monsters). This, on the other hand, will make things harder for GMs without getting rid of the basic problems inherent in resolving challenges using uniform distributions.
Of course, it could be worse. The Japanese game Double Cross uses a system of dice pools with exploding summed maxima and modifiable explosion thresholds that produces insane probability distributions. Even the most experienced statisticians would have difficulty GMing that system …
I disagree. The biggest and most intuitive use for these rolls is for making good and bad luck. On good luck, player gets advantage rolls. It’s simple and intuitive. But you are sort of right: it probably shouldn’t be used anywhere else.
If you are doing statistics, you should take a look at the J language, an array language created as a successor to APL. It is a freeware download from http://www.jsoftware.com/index.html.
Here is an example, examining the probabilities for advantage and disadvantage as discussed in the article. Note that a line of J code executes from right to left.
The probability of rolling any given number from 1 to 20 on a fair 20-sided die is 1 in 20, or 1/20. There is only one way to roll at or above a 20, which is by rolling 20 itself. So the chance of that is 1/20. To roll at or above 19, we can roll 19 or 20, so the chance is 1/20 + 1/20 or 2/20. To roll at or above 18, we can roll 18, 19, or 20, so the probability is 3/20, and so on. In J we can get the probability for rolling at or above each number on a straight d20 roll from:
straight =. (>: i. 20) % 20
where i. 20 generates the integers from 0 to 19, >: increments each of these by 1 to give 1 to 20, % is the division symbol (because / is used for something else), and =. assigns a value to a variable. The result (which we can get just by typing the name of the variable) is:
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
where 0.05 = 1/20.
Now suppose we are rolling with disadvantage. To get a score at or above a given number we must roll that number or higher on the first die AND on the second die. To “and” two probabilities we multiply them. So the probabilities of rolling at or above 20, 19, 28, …, 1 with disadvantage are:
disadvantage =. straight * straight
which gives us:
0.0025 0.01 0.0225 0.04 0.0625 0.09 0.1225 0.16 0.2025 0.25 0.3025 0.36 0.4225 0.49 0.5625 0.64 0.7225 0.81 0.9025 1
If we roll with advantage, we just have to roll at or above the desired number with either the first die OR the second die. To get this probability we first add the probability of rolling the desired number or above on either die, but then we must subtract the probability of rolling at or above that number on BOTH dice so we don’t count that probability twice. So we get:
advantage =. (straight + straight) – straight * straight
or
advantage =. (straight + straight) – disadvantage
which gives us:
0.0975 0.19 0.2775 0.36 0.4375 0.51 0.5775 0.64 0.6975 0.75 0.7975 0.84 0.8775 0.91 0.9375 0.96 0.9775 0.99 0.9975 1
We can assemble the results into a table easily enough. To generate a list of the target number for each probability, we generate the numbers from 1 to 20 and reverse them using |. like so:
|. >: i. 20
to get:
20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
We then combine all of our results with stitch (,.), using format (“:) to give us the desired number of decimal places:
2 6j3 6j3 6j3 “: (|. >: i. 20),.disadvantage,.straight,.advantage
(6j3 is the complex number 6 + 3i; for format the real part of the number is the field width, the complex part is the number of decimal places) and get:
20 0.003 0.050 0.098
19 0.010 0.100 0.190
18 0.022 0.150 0.277
17 0.040 0.200 0.360
16 0.062 0.250 0.438
15 0.090 0.300 0.510
14 0.122 0.350 0.578
13 0.160 0.400 0.640
12 0.203 0.450 0.698
11 0.250 0.500 0.750
10 0.303 0.550 0.798
9 0.360 0.600 0.840
8 0.423 0.650 0.877
7 0.490 0.700 0.910
6 0.562 0.750 0.938
5 0.640 0.800 0.960
4 0.722 0.850 0.978
3 0.810 0.900 0.990
2 0.902 0.950 0.997
1 1.000 1.000 1.000
It’s easy enough to plot the results. We first have to load the graph plotting package:
require ‘plot’
We can then generate the plot above:
plot (|. >: i. 20);disadvantage,straight,:advantage
We could also add a key and axis captions easily, though this makes the line of code much longer:
‘key Disadvantage Straight Advantage; keypos left bottom; ycaption Probability; xcaption Roll at or above’ plot (|. >: i. 20);disadvantage,straight,:advantage
or we could generate the “stegasaurus” bar plot in the referenced article:
‘bar; ycaption Probability bonus; xcaption Roll at or above’ plot advantage – straight
J has many other features that are very useful for statistical analysis, including least squares curve fitting.
Here’s a modified ggplot sequence for you (replace dat.m with your data frame name)
gg <- ggplot(dat.m, aes(x=Result, y=Prob, group=Type, color=Type))
gg <- gg + geom_line() + geom_point()
gg <- gg + labs(title="D&D 5e Advantage and Disadvantage Rolls")
gg <- gg + theme_bw()
gg <- gg + theme(legend.position=c(0.1, 0.2))
gg
Pingback: Dungeons and Dragons Fifth Edition: Not Revolutionary, but Good Anyway! | Compromise and Conceit
Pingback: Dungeons & Dragons 5th Edition and Player’s Handbook Review | Spelunking RPGs
Pingback: Ye Olde Owlbear » Gedanken zum neuen D&D – Teil 2a (Spielmechanik – Advantage)
Pingback: Building NPCs in 5e, and the Einstein Problem | dungeonhacking
Online DM commented that ADV and DIS was sort of equivalent to a +5/-5 on the rolls.
Would it be statistically better to roll a single d20 and adding/subtracting a rolled d6? I know the potential for a higher total is there, but does that offer a flatter affect over a single d20 roll? The second d20 increases the possibility of a pass at the lower targets than at the higher targets, and is inverse for disadvantage. I would think that you would want the same relative boost/penalty throughout the range of possible targets and rolls.
Okay, so on Facebook D&D boards we recently started talking about whether taking two attacks was better than taking one attack with advantage. I can’t figure out the math to prove it though. It seems to me that in both cases, you are rolling two d20’s with the same bonus. But with two weapons, all the times both dice would hit result in more damage, while in advantage, if both dice roll “hits” that doesn’t yield any more outpout, therefore, two weapons must be better. But how much better?
Say your average weapon damage is ‘d’. eg 1d8+2 -> 3 to 10 -> average 6.5 damage.
prob(hitting normally) = p
Expected damage from two attacks is p.d + p.d = 2.d.p
Expected damage from one advantaged attack = d.p* … p* being the greater probability of hitting with advantage.
From the table above, p* is never going to be larger than (p + 0.25) and by adding a ‘2p’ column to the table above you can see that 2p is uniformly greater than p*.
From 20 down to 1, 2p is greater by: 0.2%, 1%, 2.2%, 4%, 6.2%, 9%, 12.2%, …
Translating this: yes, two attacks are always better. How much better varies on your chances of hitting – if you have a low chance of hitting, two attacks are a tiny bit better; if you have a high chance of hitting, two attacks are significantly better.
This is assuming that all attacks are equal; if the attack with advantage has higher damage, or stronger riders, than the two attacks without, that changes the maths.
Pingback: Game Theory: Shooting Into Melee | Basement Dwellers Gaming Club
The better “non-rule” would be to roll To Hit normally with the arrow shot. If they miss, then roll again To Hit the friendly target, using the appropriately adjusted armor class (i.e. no shield or perhaps no Dex modifier for a back attack). While there are still two rolls, other variables of hitting a different target, like armor, magical protection, etc. are taken into account.
Pingback: More Advantages to Advantages – Or How I Learned to Stop Worrying and Love the d20 | Rolling the Hard Six
Your table only goes 3 places past the decimal point, skewing the results. For instance rolling a 20 with disadvantage shows as “.002” (1/500) when in fact it should be .0025 (1/400). A significant difference.
…you DO realize that this is simple statistics, right?
Advantage: P(a or b) = P(a) + P(b) – P(a) x P(b)
Disadvantage: P(a and b) = P(a) x P(b)
Since P(a) = P(b), this becomes:
Advantage: P(a or b) = 2 x P(a) – P(a)^2
Disadvantage: P(a or b) = P(a)^2
In game turns, the chance of getting a roll equal to AC or above becomes:
Normal: (21-AC)/20
Advantage: (42 – 2AC) / 20 – ((21 – AC)/20)^2 = (21 – AC) x (AC + 19) / 400
Disadvantage: (21 – AC)^2 / 400
To calculate the chance of hitting an enemy, simple take their AC, adjust with modifiers (e.g. if you have +5 to hit, lower AC by 5), and input into the relevant equation. No tables or simulations needed.
Greaat!
Pingback: Homebrew Rule: The MVP Award - Dungeon Solvers
Pingback: Probability – Heroes Rise
Pingback: What is the Best Basic Die Roll for D&D 5th Edition? A Probabilistic Analysis | Compromise and Conceit
this is all wrong.
2 0.903 0.950 0.998
so u say that i have 95% of rolling above or equal with d2 without advantage? lets see…
1 – 1
1 – 2
2 – 1
2 – 2
for me this is only 75% chances so u made a fatal mistake in ur calculations. sorry.
No — there’s no d2 involved anywhere. What it means is that in 5e, rolling a d20 with disadvantage gives you a 0.903 chance of rolling 2 or higher. Without advantage or disadvantage, you have a 0.950 chance of rolling 2 or higher on a d20. With advantage, you have a 0.998 chance of rolling 2 or higher on d20.
What is in between the probabilities of rolling 6 and 8 w/ adv. and disadv.? Why is there a blank space there?
Thanks for this! Came here to see my chance of having my concentration spell interrupted. I have Warcaster (advantage on CON saving throws), and Resi: Con feat, so +7 on my CON saving throw. so I need to roll a 1 or 2 on BOTH of my saving dice to have my spell interrupted, so only a 1% chance.
You’ve made me happy. :)
Pingback: DnD Dice - Master The Dungeon's Complete Guide to Dice
No, that’s statistical probability and numbers mean absolutely jackshit when the dice are rolled. You are more likely to roll really low twice, and that Astra role does not actually amount to a bonus. If I roll two tens those are still tens. If I needed a 15, a plus 5 on a single roll would have helped. That second roll which was also too low it’s completely useless. Advantage sucks
We use critical miss and hit at our table.
library(dplyr)
library(reshape2)
library(ggplot2)
to.hit <- seq(5,30,5)
mods <- c(-5,0,5,10)
n.sims <- 50000
df <- data.frame(expand.grid(to.hit, mods, 1:n.sims, c("no.adv", "adv")))
colnames(df) <- c("dc", "mods", "n.sim", "adv")
df %
mutate(base.roll = sample(c(1:20), n(), T),
mod.roll = base.roll + mods,
crits = if_else(base.roll == 20, 1,
if_else(base.roll == 1, -1, 0)),
hit.res = 1*(mod.roll >= dc),
hit = (crits + hit.res) > 0
)
res.df %
mutate(either = 1*((hit.no.adv + hit.adv) > 0) )
results %
group_by(mods, dc) %>%
summarise(no.adv.ct = sum(hit.no.adv),
adv.ct = sum(either),
no.adv.pct = sum(hit.no.adv)/n(),
adv.pct = sum(either)/n()
)
ggplot(results, aes(dc, adv.ct/no.adv.ct, color = as.factor(mods))) + geom_line() +
scale_x_continuous(breaks = seq(5,30,5)) +
scale_y_continuous(breaks = seq(1,3,0.125)) +
labs(color = “Modifiers”) +
xlab(“Difficulty”) +
ylab(“Advantage/no advantage ratio”) +
theme_grey()