I’ve said it before and I’ll say it again: interaction is one of the key underrated topics in statistics.
I thought about this today (OK, a couple months ago, what with our delay) when reading a post by Dan Kopf on the exaggeration of small truths. Or, to put it another way, statistically significant but not practically significant.
I’ll give you Kopf’s story and then explain how everything falls into place when we think about interactions.
Here’s Kopf:
Immediately after an album is released, the critics descend. The period from the first to last major review for an albums typically falls between 1-6 months. As time passes, the average review gets slightly worse. Assuming my methodology is appropriate and the data is accurate and representative, this is very likely a statistical truth.
But is this interesting? . . .
My result about album reviews worsening over the review periods is “statistically significant.” The p-value is so small it risks vanishing. My initial response to the finding was excitement and to begin armchair psychologizing on what could be causing this. I even wrote an extensive article on my speculations.
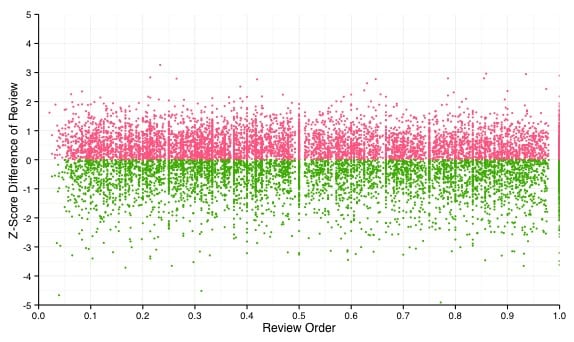
But I [Kopf] was haunted by this image:
Each point is a review. Red ones are above average for that album, and green ones below. . . . With so many data points, it can be difficult for the human eye to determine correlation, but your eyes don’t deceive you. There is not much going on here. Only 1% of the variation of an album’s rating is explained by knowing when in the order of reviews an album fell. . . .
Is 1% worth considering? It depends on the subject matter, but in this case, its probably not. When you combine the large sample sizes that come with big data and the speed of modern computing, it is relatively easy to find patterns in data that are statistically significant . . . . But many of these patterns will be uninteresting and/or meaningless for decision making. . . .
But here’s the deal. What does it mean for the pattern to be tiny but still statistically significant? There are lots of albums that get reviewed. Each set of reviews has a time trend. Some trends go up, some go down. Is the average trend positive or negative? Who cares? The average trend is a mixture of + and – trends, and whether the avg is + or – for any given year depends on the population of albums for that year.
So I think the answer is the secret weapon (or, to do it more efficiently, a hierarchical model). Slice the data a bunch of ways. If the trend is negative for every album, or for 90% of albums, then this is notable, if puzzling: how exactly would that be, that the trend is almost always negative, but the aggregate pattern is so weak?
More likely, the trend is positive for some, negative for others, and you could try to understand that variation.
The key is to escape from the trap of trying to estimate a single parameter. Also to point out the near-meaninglessness of statistical significance the context of varying patterns.
Although it is perhaps worth adding that if you want to go hierarchical and estimates all the relevant parameters, you’d better make sure you have enough data to do that estimation. People blindly go ahead and fit hierarchical models with dozens of parameters, which the data has no chance of giving a reasonable estimate on (Bayesian HLMs with appropriately agnostic priors will often take care of that, but so far not many people are fitting such Bayesian HLMs).
Shravan:
Yes, when data are weak it can be important to include informative priors. Jennifer and I did not make this point in our book, which was a mistake on our part.
Oh, but isn’t that often treated as a feature & not a bug. Dozens of parameters let you tweak the fit and give you just that additional degree of freedom to coax the model to conclude what you want it to?
At least in my own research, additional parameters are often variance components, so if you are thinking of the equivalent of p-value hacking, the result will often end up as “no effect” if you add more and more variance components. Or maybe you mean tweaking the priors? Yeah, one could always set up the Bayesian equivalent of p-value hacking, prior-hacking. But one would just make a fool of oneself if one did that, because one will have to mention the priors, and will get caught out.
Hi Andrew, the link to Kopf’s article doesn’t seem to be working.
Tim,
Yeah, I have no idea why the post got taken down.
Tim and Andrew,
I removed the post from my blog a couple weeks ago because I was not sure it was of high quality. I have reposted. I will also test out Andrew’s ideas on my dataset and follow up.
– Dan
It’s still cached at Google (dated 2 April 2015).
Clinical trials that show a small but significant result have always puzzled me. If the experimental arm provides a tiny improvement for each patient, it probably does not mean much clinically. If it means that the experimental arm leaves most patients the same but provides a real difference for a small number, then one should pursue this in order to define the population that will benefit. It is like finding a tiny gold nugget; is the gold randomly scattered and not worth chasing, or is there a valuable gold vein?
Do my examples fall into your categories, and can you suggest ways to understand such trials better?
David Cox has a nice paper on interactions in epidemiological contexts. It focuses on interpretation rather than method, but it might be useful:
http://projecteuclid.org/download/pdfview_1/euclid.aoas/1196438023
I’m not sure this is a useless result. Suppose, for example, we could predict that if the average review was 4.5 after 1 month, it will eventually be 4.3. So, in weighing a new release versus an older release, 4.5 would be the equivalent of 4.3.
We ignore the noise of individual observations all the time, and find the results useful. The average December temperature in Chicago is 26F, the average January temperature is 21F, and it’s certainly meaningful to state that January is usually colder than December. But if we looked at individual days for a set of years, the individual observations would have large variability — I’ll have to look at my daily weather database to see if that, also, is about a 1% effect.
A hierarchical model is probably a good idea. For one thing, it may be that certain types of material decline, others increase — maybe hot sellers tend to increase, or country albums [etc]
@zbicyclist:
Isn’t the Dec-Jan temperature difference you describe more on the order of 20% than 1%?
Maybe if someone tried claiming that Christmas eve is warmer than Christmas you’d get an analogous situation?
On the Kelvin temperature scale 26F = 269.8167K and 21F = 267.0389K. Thus
(269.8167K-267.0389K)/269.8167K = 1.03%
@Rahul. In order to make ratio comparisons (i.e. %) on temperature, we need to Kelvin, not Farenheit, because Farenheit is an interval scale and Kelvin is the required ratio scale. So we are comparing 267.039K with 269.817K. This is a difference of 1.04% — which Andrew would recommend rounding to 1%.
So, obviously, I had carefully picked my comparison to be appropriately calibrated. [insert multiple smiley faces here] No, I got lucky. But I was looking for a case where the individual variability is very high relative to the average.
So if I plotted temperatures on a Farenheit scale & noticed “by eye” that Jan is indeed cooler than Dec. do I have to then replot the data using Kelvins to make me un-notice that trend? :)
We’re talking about 1% of the total observed variation (in this analogy to the album reviews), so Kelvin, Fahrenheit or Celsius, doesn’t matter. What is the 5° difference in proportion to the total variation in measured temperature (in Chicago, not the universe) – that is the question.
(still using this to avoid other things I should be doing).
From the NOAA site, I downloaded daily O’Hare Min and Max temperatures (in tenths of a degree Celsius) from Jan 1, 1973 to December 2, 2014. I calculated the average temperature of each day as the average of the minimum and maximum temperature.
The average difference between December and January is 27.5 (tenths of a degree Celsius), which is 4.9 degrees Farenheit.
The variance of the average Chicago daily temperature is 12,318 if we consider the entire year, 4350 is we consider just December and January.
If we run a dummy variable regression on just the January and December data, the R-square is 4.3%. If we consider this in the context of the entire wonderful 12 months of Chicago weather (with 3 times the variance) the December-January difference is 1.5%.
More likely, the trend is positive for some, negative for others, and you could try to understand that variation.
In other words, conditioning on covariates (which may or may not exist).
another reminder that a regression coefficient usually refers to mean change, and not an actual process. Take the average net weight gain of 10 pounds per decade for Americans. Not only is there substantial variation, making it unclear what subset of the population is accurately described by that rate, but even for people with net 10 pounds per decade, the actual process of weight change was something entirely different. People are losing and gaining weight in 5-10 pound swings all the time, often multiple times per year. That’s the process.
but the small changes movement said “gee, 10 pounds per decade works out to about a 10 kcal energy imbalance per day. Let’s try to figure out how we can rectify a 10 kcal per day imbalance.” Wrong way to frame the problem, wrong way to characterize the process. But it is very very easy to fall into the trap of reading a regression coefficient in a table and thinking of it as a description of the change process.
GWAS GWAS GWAS
Gesundheit!
@Shravan:
Not sure if it would be so easy to get caught as you think. The set of “reasonable looking” priors isn’t small, is it?
You can only mention the prior you ended up choosing. What about all those priors you tried out but dumped because the results looked meh?
Share your data and stan (or whatever) code and people can easily re-run it under different assumptions. That is, it may be better to move away from the view that a paper is a perfect one-off static result towards a more dynamic view of ‘objectivity’.
+1. You said it better than me.
As I understand it, any complete Bayesian analysis is going to include a sensitivity analysis. I always check that my priors are not having any undue influence on the posterior. For specific domains, the priors might be fairly easy to limit to a few plausible categories. For example, in reading time studies if you define a uniform prior on sigma (error sd), then the bounds on the uniform distribution are pretty easy to define (within specific labs at least).
When I have large amounts of data, no amount of messing around with priors is going to have any effect on the posterior. In those case I don’t report my sensitivity analysis in any detail, I sometimes just mention that under such and such priors the result remains unchanged, and sometimes I just don’t mention it at all. Anyway, I always release all data and code on publication of datasets that I wrote the analysis code for myself, so anyone can go and check if there is a sensitivity to prior specification. People really need to just start releasing all their data and code as a matter of course. I have only about 25% success in getting raw data from published work.
Shravan:
All good, but check the sensitivity to your data model (the “likelihood”) too!
Yes, sure, always! Closely related to this point: in the next revision of Gelman and Hill please, when you tell the reader that the normality assumption of residuals is the least important thing, please also add that you are not talking about statistical inference using p-values! People in psycholinguistics justify ignoring the normality of residuals when doing NHST, citing Gelman and Hill. I know that in your “tips” section in the book you provide more guidance on such things, but apparently nobody really reads the whole book ;).
It’s actually a strange irony that people cite statements in Gelman and Hill to justify procedures that Gelman vehemently rejects. I guess you didn’t come down hard enough on NHST in that book, so your earlier chapters could be seen as an endorsement rather than a pedagogical tool as an entry point into Bayesian methods.
I’m ranting about this because I’m teaching a course this semester using your book, and am re-reading it. Reading it in 2015, having nearly completed a formal introduction to statistical theory, I have a much better understanding of the material in that book; when I read it first in 2007 or so, I didn’t really understand a lot of the details.
FYI, the figure and the link to the Bowers and Drake paper for “The Secret Weapon” no longer work…granted it is from 2005.