In a news article entitled “Why smart kids shouldn’t use laptops in class,” Jeff Guo writes:
For the past 15 years, educators have debated, exhaustively, the perils of laptops in the lecture hall. . . . Now there is an answer, thanks to a big, new experiment from economists at West Point, who randomly banned computers from some sections of a popular economics course this past year at the military academy. One-third of the sections could use laptops or tablets to take notes during lecture; one-third could use tablets, but only to look at class materials; and one-third were prohibited from using any technology.
Unsurprisingly, the students who were allowed to use laptops — and 80 percent of them did — scored worse on the final exam. What’s interesting is that the smartest students seemed to be harmed the most.
Uh oh . . . a report that an effect is in one group but not another. That raises red flags. Let’s read on some more:
Among students with high ACT scores, those in the laptop-friendly sections performed significantly worse than their counterparts in the no-technology sections. In contrast, there wasn’t much of a difference between students with low ACT scores — those who were allowed to use laptops did just as well as those who couldn’t. (The same pattern held true when researchers looked at students with high and low GPAs.)
OK, now let’s go to the tape. Here’s the article, “The Impact of Computer Usage on Academic Performance: Evidence from a Randomized Trial at the United States Military Academy,” by Susan Payne Carter, Kyle Greenberg, and Michael Walker, and here’s the relevant table:
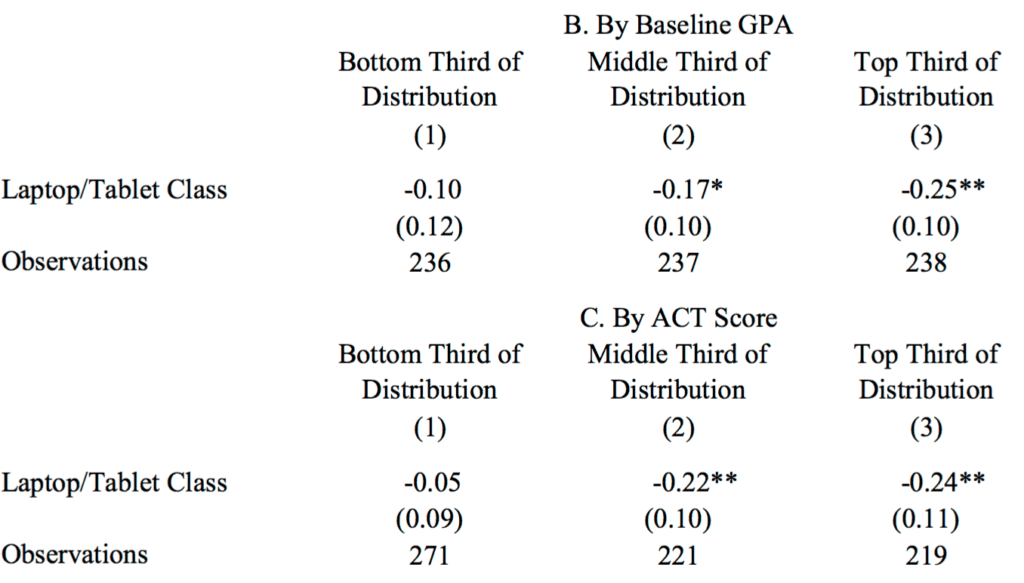
No scatterplot of data, unfortunately, but you can see the pattern: the result is statistically significant in the top third but not in the bottom third.
But now let’s do the comparison directly: the difference is (-0.10) – (-0.25) = 0.15, and the standard error of the difference is sqrt(0.12^2 + 0.10^2) = 0.16. Not statistically significant! There’s no statistical evidence of any interaction here.
Now back to the news article:
These results are a bit strange. We might have expected the smartest students to have used their laptops prudently. Instead, they became technology’s biggest victims. Perhaps hubris played a role. The smarter students may have overestimated their ability to multitask. Or the top students might have had the most to gain by paying attention in class.
Nonononononono. There’s nothing to explain here. It’s not at all strange that there is variation in a small effect, and they happen to find statistical significance in some subgroups but not others.
As the saying goes, The difference between “significant” and “not significant” is not itself statistically significant. (See here for a recent example that came up on the blog.)
The research article also had this finding:
These results are nearly identical for classrooms that permit laptops and tablets without restriction as they are for classrooms that only permit modified-tablet usage. This result is particularly surprising considering that nearly 80 percent of students in the first treatment group used a laptop or tablet at some point during the semester while only 40 percent of students in the second treatment group ever used a tablet.
Again, I think there’s some overinterpretation going on here. With small effects, small samples, and high variation, you can find subgroups where the results look similar. That doesn’t mean the true difference is zero, or even nearly zero—you still have these standard errors to worry about. When the s.e. is 0.07, and you have two estimates, one of which is -0.17 and one of which is -0.18 . . . the estimates being so nearly identical is just luck.
Just to be clear, I’m not trying to “shoot down” this research article nor am I trying to “debunk” the news report. I think it’s great for people to do this sort of study, and to report on it. It’s because I care about the topic that I’m particularly bothered when they start overinterpreting the data and drawing strong conclusions from noise.
Don’t you get somewhat more evidence (admittedly still not nearly conclusive) from the ordering? Only one third of roughly equal effects will be ordered (either up or down). I don’t you think you have two separate orderings here because of the correlation of GPA and ACT score, but the uniformity of direction isn’t being accounted for in your simple use of the standard errors.
You could fit a straight line through the three points, which actually fits very well (at least for the top part of the table). However, the slope is still not significantly different from 0, even if you were to test one-sided.
Sure… that’s what I meant by “not nearly conclusive.” My point, though, was that by merely looking at the effect sizes and the standard errors in the three groups you are understating the evidence the data are giving you.
The binning makes it impossible to get a significant effect here, but it is just barely possible that a non-parametric (or even linear) fitting of the raw data might show a real trend. If it did, then the authors’ point might be correct even if their reasoning from the three-bin results is invalid.
The higher up you sit the further you can fall?
Rahul:
No, no! This is the whole problem. You’re coming up with an explanation for something that can just as well be explained by pure noise.
I know! But this is soooooooo tempting, the armchair theorizing. :)
I think if you can imagine someone tweeting the main conclusion of a study with little flame emojis it’s a signal to be mistrustful of the stats.
:flame: smartest students harmed most by classroom laptop use!! :flame:
:flame: a 15-minute conversation can eliminate homophobia! :flame:
:flame: ESP IS REAL :flame:
While the paper has gone to great lengths to do multiple analyses, and apparently there is still plenty to criticize, I find one of their qualitative conclusions the most disturbing. The examine dependent variables of multiple choice questions, short answers, and essay questions. They conclude “Taken together, the evidence in Appendix Table 1 indicates that essay scores do not provide an accurate measurement of student achievement.” Presumably this follows from the fact that “professor fixed effects explain 32 percent of the variation in essay question test scores.” After 35 years of teaching, I am insulted to discover that professor fixed effects render the use of essay questions (which are the only type I have asked for the past 34 years) to be inaccurate measurement of student achievement. I’m glad I’m near the end of my teaching career and not the beginning!
I’m ignorant: what does “professor fixed effects explain 30% of the variation” actually mean?
professor fixed effects = including dummy variables for professors
I hope the professors on the list see the humor in using dummy variables for professors.
+1
I think they’d call them ‘indicator variables’ instead
If they’re making a cross-class comparison, then yes, essays might not be a useful measurement because of changing the professor, but that doesn’t necessarily mean that essays are useless for cross-student, within-class comparisons. I’d still be wary of essays as a measurement technique just because if they can’t be validated across professors, then that is evidence that the measurement is not valid within a class as well.
Somebody can undoubtedly do a better job of explanation, but my take is that the professor grades the essays and sees prior test scores, so it is possible that there is a bias due to that. So, the professor’s identity is included in the model and has a significant effect on the scores. Hence, the unreliability of essay exams as measures of student achievement!
Of course, there is no other reason why the professor might make a difference and it is not possible that the difference would emerge on essay questions but not on multiple choice or short answers – which is why I’m glad I am nearing the end and not the beginning of my career. All this time I thought I made a difference and that essay exams were the best way to see that. How foolish of me.
I’ll be the devil’s advocate here and say, a contrario, the effects are not small, the sample sizes are not small either (700 total, >200 in each of three subgroups), and there is no evidence of fishing for significance (specification searching) by testing multitudes of possible effects and reporting only that which is significant. It seems to me a straightforward and well done experimental design based on a simple and plausible idea. If this isn’t good enough, I don’t know what is.
But I will grant you that they probably over-interpret the results. Sadly, this is how research gets published. The Dragnet approach (“Just the facts ma’am”) doesn’t lead to publications. You need a story, and that often means over-interpreting.
Are the sample sizes not small? How big is small? How small is big? I dunno, man. And how do you know there’s no specification search? You don’t have their Stata logs.
You have to think of sample size in the context of the statistical power to detect a certain effect size, or differences in effect size between groups.
The design seems perfectly fine, I think the real issue here is that the analysis approach is wrong for several reasons:
1) NHST is a lousy scheme, statistical significance of differences is not our goal.
2) Instead of using GPA and ACT as combined predictors, they’re analyzing them separately (more noise)
3) Instead of doing a nonlinear regression analysis they’re analyzing binned data, poor choice of basis functions to represent a continuous effect
The paper is long and full of tables (Where are the damn figures!) and doesn’t seem to include the dataset itself, but I can easily imagine them having a more convincing result if they did a simple model like
score/score_max ~ logistic_function(polynomial((ACT/ACTMAX+GPA/GPAMAX)/2 – mean_pre_score, a,b,c,d))
where polynomial is a 3rd order polynomial with coefficients a,b,c,d and the logistic function ensures the function stays within the 0,1 range
I think this is once again a problem of representing a continuous function as discrete steps, as per our recent discussion of seasonal effects
http://models.street-artists.org/2016/05/02/philly-vs-bangkok-thinking-about-seasonality-in-terms-of-fourier-series/
Also a nice simple scatter plot of the data along with the fitted curves would be very useful. And obviously, you fit this curve separately in the two groups, and plot the two groups in different colors, and you do it in Stan with informative priors on the coefficients, and show a separate spaghetti plot of samples of the difference between the two curves to show whether there’s discernible differences in performance across the range of the pre-grade predictor
What’s annoying is that popular coverage / abstracts of articles of this nature never give the effect size.
How is “students who were allowed to use laptops scored worse on the final exam” very useful to know unless you tell me how much worse? Was the test score difference 1%? 50%?
Huge difference in implications!
I’m sure the answer is always buried in some table deep inside the paper but the summaries / popular coverage / abstract never ever seems to have that bit of info!
Agreed, but I think this isn’t just the popular news, it’s part of the NHST focus, it’s present in many scientists view of what they’re doing: we tested and found a *significant* difference, and that’s all that matters, jackpot, bingo, whoohoo!
I’ve even had some biologists tell me “we don’t really care what the size of this difference is, just that there is a difference” which just reflects how little data they normally have, if they routinely collected enough data to detect statistically significant differences at well below anything they’d practically care about they would realize how insane that idea is.
suppose they are looking for expression level data in a gene… and they collect 1 million data points and find that under some condition there’s on average 1.00000022 times as much of the gene as in control conditions… and this happened routinely… they would finally understand what’s wrong with p values. Instead they routinely collect only enough data to maybe sort of detect around 2 or 3 times the reference condition which is a very biologically plausible practical difference, and so they basically think that detecting a difference and having a meaningful difference are pretty much the same thing.
yep, and the other practical problem in biology/ecology is that there is very little understanding of type M errors. Most applied researchers adopt the binary thinking that: a) if “non-significant” ignore everything, and b) if “significant” take effect size literally. Without having done a lot of simulations to play with random variables and study type I/II errors, it is difficult to get the right intuition for what is going on with statistical power and the very real implications it has for getting magnitudes of effects right…
Chris
One of the reasons for this I think is that many Biological hypotheses are basically qualitative anyway “if you knock out this gene you’ll probably fail to form a proper retina” and “in the presence of androgenic hormones you’ll have more expression of gene X” etc.
So, when looking for quantitative evidence of this kind of qualitative idea they have a hard time figuring out “what to do” with specific quantities. So, gene X is expressed at 120% of reference level, does that really mean you were “right” or “wrong” about your qualitative hypothesis??
Daniel, I think you are right, particularly in molecular biology. But at the levels I work at (population, community, ecosystem), many (maybe most, I’d have to think more about it) interesting questions are quantitative, i.e. sorting through the magnitude of effect of various invasive species on native biodiversity or something like that. Usually, big real-world datasets I’ve got my hands on are WAY more variable/noisy then the “textbook” theory suggests. I used to think this was just due to experimental demonstrations being done in simplified conditions compared to natural ecosystems, but increasingly I suspect that the statistical significance filter is a big part of it. There’s a tendency to believe claims of X% reduction in Y, b/c in peer-reviewed literature with p < 0.05, the same stuff Andrew Gelman writes about in social psych. etc. I've also seen a lot of focus on statistically significant sub-groups, interactions, and then of course tools like structural equation modeling which are an open invitation to story-telling…
@Chris
I would limit “quantitative” questions to ones in which an actual effect magnitude is predicted, for example, the different models of metabolic or biomechanical scaling generate different scaling coefficients, so no one gets excited about “an effect” (the existence of a slope different from zero) but only about confidence intervals covering some predicted value. I don’t see these kinds of quantitative predictions in much of community ecology. Instead, hypotheses predict the existence and sometimes directions of effects but not their magnitude. In some (too many) community ecology papers, P-values are given without any reporting of effect size. In most papers with effect sizes reported, the magnitude is reported without any discussion of the importance or consequence or relevance of this magnitude to the system. In my reading of that literature, the emphasis is still on IF there is an effect, but some (even many) do at least report the size of the effect. But I would not consider merely reporting the size of an effect testing a quantitative question.
The more usual practice in areas like molecular biology is to do an experiment 3-5 times and drop any results you don’t like because “something got messed up somewhere”. Repeat this process until you have 3 results you like. As far as I can tell most do not realize it may cause any conflicts with their “hypothesis” testing. Then of course all of the trying out different analyses and other forking paths stuff.
This got me thinking, maybe it would be helpful to figure out a “significance magnifier” statistic: If you treat your data in this way (dropping outliers, trying out different analyses, etc), it is like you increased your sample size by 1,000x when it comes to determining statistical significance. In that scenario, a difference of .001 kg between males and females would be statistically significant. So your observed difference of 10 kg isn’t very impressive.
I think measuring “impressiveness” by a p value is just a wrongheaded idea and should be scrubbed from science.
The biggest issue, like I say above, is that we need quantitative thinking at the substantive hypothesis level in biology. Then you can actually figure out what your quantitative data means.
In the past when I have had a say in such things we typically have used Bayesian methods with something like a t distribution for errors to account for the fact that “something can get messed up” and produce *really* different results occasionally. I think the dropping out stuff is more or less a response to typical canned analyses that use normal error models that fail to be appropriate when it really is possible that someone damages a certain batch of enzyme by leaving it on the hot plate accidentally or whatever.
Doing a canned, unregularized ANOVA when you have say 4 results like 100,90,79,0.25 really doesn’t help you discover anything even if using all the data is in principle the right thing to do. Lack of good tools to handle messy data is responsible for a lot of what you describe I think.
Responding to your two posts at once:
“The biggest issue, like I say above, is that we need quantitative thinking at the substantive hypothesis level in biology. Then you can actually figure out what your quantitative data means.
[…]
Lack of good tools to handle messy data is responsible for a lot of what you describe I think.”
Yes, and yes. I think these are 2/3 issues at the root of all problems currently facing biomed research, the other being the lack of routine *direct* replication studies.
Regarding quantitative thinking, afaict this is a matter of effort. Or else how do we have the Armitage and Doll model of carcinogenesis, all the variants of SIR models of infectious disease, the relationships between cardiac output and blood pressure, Thurstone and Gulliksen’s work on learning curves, etc. These are all quantitative models come up with before most current biomed researchers were born. It is not impossible to do it! Now, there is surely a sociological aspect here. How can someone who tries to think deeply enough about their theory compete in terms of publications/year with someone who gets away with significant p-values?
Regarding tools to deal with messy data, there has been a long-standing miscommunication between people collecting data and what statisticians are offering to analyze that data. It seems to me neither community really understands the limitations of what the other can do. Once again this is sociological.
This brings us to the third issue of performing replication studies. These are simply crucial, you cannot sustain progress without them. The reason being that in reality the data is messy, the analysis is ad hoc, and you need to predict what happens with new data to tell if you are on the right track. The only *real* way to test a hypothesis is to make a precise prediction (it doesn’t have to be that precise, it could just be upper or lower bounds), and compare it to new data.
Interesting point: Are Bayesian papers more likely to explicitly declare their effect size in their Abstracts? I wonder.
Maybe we’re reading difference sources, but in my experience ‘popular coverage’ usually does include an effect size — it maybe gets less attention than the binary yes/no finding (which typically goes right in the headline), but it’s there. The WaPo blog Andrew links, for example, devotes a paragraph to stating the effect size and another one to contextualizing it.
The paper itself doesn’t bury the the effect size either — it’s right there in the second sentence of the abstract — and I don’t feel like I encounter many that do.
If your mindset is all fixed around NHST it pretty much demands that you segment your data into groups even if there is a perfectly reasonable continuous structure, it really damages people’s brains into thinking (I’ve got to define two groups so I can find out whether there’s a difference in average between them according to Stata!)
If on the other hand you are thinking in a model based way about how the pre-class grade/score informs what you found in your results, it becomes obvious that *at every point* along the “x axis” (GPA/ACT score) there’s a potential difference between the two groups which is subject to measurement error… and off you go towards fitting curves and seeing whether in some portion of the continuum there’s a sufficiently large and consistent difference to call it out. It also makes it clear how to use a Bayesian result: from the samples, compute the difference *in the curves* not *in the coefficients* (hence spaghetti plots of differences).
Here’s a little experiment I did recently. Generate a normally-distributed set of values, say with mean = 0.0 and sd = 1.0. Use the observed sample mean and sd to compute the p-value of the result. Then repeat, say, 1000 times. Now you have an approximation to the distribution of p-values. And it’s not remotely normal.
In fact, it’s linear. So most of your statistical intuitions about its properties are going to be wildly wrong.
(BTW, if you compute those p-values using the actual theoretical sd (that is, 1.0) instead of the sample sd, the distribution is quite different and more centralized.)
You expect p-values to be uniformly distributed under the null, no?
Yes … if p = 0.05 means that 5% of the time you will get those results, then it ought to be a uniform distribution: 10% of the time you will get p = 0.1, etc.
Point is not so much that the distribution is expected, more that I hadn’t thought much about what distribution to expect until now. And that distribution is very non-gaussian.
Tom, the sort of simulations that you ran are great for exploring the nature of P-values and for tuning your intuition. You might be interested in the relationship between P-values and likelihood functions that can be exposed by them https://arxiv.org/abs/1311.0081.
Also: http://www.p-curve.com
I think my comment earlier disappears, so here goes attempt no. 2:
With the caveat that I’ve only glanced at the paper, I don’t see how your criticism is valid. It’s clear from the abstract and tables that it is *not* the case that the authors only find an effect if they divide their subjects into particular groups. Rather, there’s notably worse performance by the laptops-in-class group; again, this is the claim that’s made in the abstract. *In addition,* one can look at sub-groups and poke around — this seems to be a minor point of the paper.
Furthermore, even if one argues that they shouldn’t be looking at sub-groups, your criticism that the authors make the mistake that “The difference between “significant” and ‘not significant’ is not itself statistically significant” seems wrong. It’s not that they are comparing the different GRE/ACT-scoring groups with each other, but rather comparing e.g. high-level students in laptop-classes with high-level students in no-laptop classes. Your simple adding-the-variance calculation isn’t actually adding the relevant variances. (It’s possible my quick reading is incorrect; feel free to correct me.)
Overall, your characterization of this seems rather irresponsible.
The paper does report on differences between the ‘smart’ and ‘poor’ student subgroups, and it offers a few lines of speculation for what might be driving those differences (other than noise). That said, they also acknowledge that, “the point estimates […] are statistically indistinguishable, so these could be chance findings.” In essence they’re saying, “this could be noise, but if it’s not, here’s what we think might be going on.” I see no problem with that.
They’re also not really hyping up or focusing on those subgroup differences… it’s not mentioned in the abstract, nor at any point in the conclusions, from what I can see. Their focus is on the result that laptops decreased performance overall, which nobody seems to have a problem with.
The WaPo blog post is another matter; the writer there zeros in on the subgroup comparisons as the most interesting part of the paper, and fails to acknowledge that the comparisons aren’t statistically significant. It’s not really clear whether the target of Andrew’s criticism is the blogger or the original authors, but to the extent it’s aimed at the bloggers I think it’s well-founded.
One could also argue that the blogger’s error represents a failure of communication on the part of the study authors. Personally I think that’s a little too harsh, in this case.
Crh:
I disagree. Sure, I agree that it’s better for researchers to give caveats if they’re going to interpret what could be noise, but the problem here is selection. If you want to interpret non-significant comparisons, you should look at all of them. To select a subset of comparisons based on a difference between significant and non-significant is just noisy. To put it another way, think of all the other non-significant differences in the data. Don’t they deserve interpretation too. If you let your choice of what to interpret and what to conclude be driven by comparisons of significant to non-significant, you’re chasing noise.
Okay, that’s fair. I still think the original paper explicitly demonstrates an understanding that, “the difference between significant and not significant is not itself statistically significant,” so I don’t think they chose to report those particular comparisons for that reason. But I guess it doesn’t really matter whether their selections were motivated by a misunderstanding of statistics or by some other arbitrary criteria (e.g., perhaps the non-significant differences they reported were more interesting than the ones they didn’t); there’s an overinterpretation problem either way.
Raghuveer:
The statement, “What’s interesting is that the smartest students seemed to be harmed the most” (which was made in the news article, not in the research article) is a comparison between different groups of students. The comparison could be expressed as (A2 – A1) – (B2 – B1). But the conclusion is based on A2-A1 being statistically significant, and B2-B1 being not statistically significant. This is an error.
Similarly, the statement quoted above, “These results are nearly identical,” makes the statistical error taking a non-significant difference which, just by chance, happens to be very close to zero in the sample, and claiming this maps only to a small difference in the population.
By saying that the authors of this paper made two common errors, I’m not saying I think the paper is terrible. I just think they made some errors. I’m not “characterizing” the paper in any general sense, I’m just noting some mistakes, mistakes which are commonly made and which I think it’s instructive for me to point out. I don’t see what’s irresponsible about that!
And please see again the last paragraph of my above post where I emphasize my support for this sort of research.
It’s maybe a bit much to expect these people to put up open data before their paper is even published in final form, but does anyone know if the data *is* in fact available?
Openness at West Point? Oxymoron?
You probably need a security clearance to go and meet the author.
Rahul:
I spoke at West Point a couple years ago and I don’t recall that any security clearance was needed.
Tables of actual data and basic graphs – scatter plots, etc. – should be mandatory. It bothers me to skim over all the writing to reach the data appendix only to find it’s almost entirely reporting of their regressions instead of actual data and plotting.
An easy way I like to think about why you can’t compare a statistically significant effect to one not statistically significant is to consider a simple thought experiment. I hold in each closed hand one type of coin. Your task is to determine the denomination of the two coins, which could be different or equal. I open only one hand exposing the denomination of one coin, while keeping hidden the denomination of the other. You perform an experiment by looking at my hands, revealing to you with “statistical significance” the denomination of the coin in the open hand. You do not have sufficient data to ascertain with any confidence the denomination of the coin in the closed hand. One is statistically significant, the other is not, but you certainly can not say that the two denominations are different because of this.